2021-08-26:长度为N的数组arr,一定可以组成N^2个数字对。例如arr = [3,1,2],数字对有(3,3) (3,1) (3,2) (1,3) (1,1) (1,2) (2,3) (2
2021-08-26:长度为N的数组arr,一定可以组成N^2个数字对。例如arr = [3,1,2],数字对有(3,3) (3,1) (3,2) (1,3) (1,1) (1,2) (2,3) (2,1) (2,2),也就是任意两个数都可以,而且自己和自己也算数字对,数字对怎么排序?第一维数据从小到大;第一维数据一样的,第二维数组也从小到大,所以上面的数值对排序的结果为:(1,1)(1,2)(1,3)(2,1)(2,2)(2,3)(3,1)(3,2)(3,3)。给定一个数组arr,和整数k,返回第k小的数值对。
福大大 答案2021-08-26:
1.暴力解。
时间复杂度:(N^2 * log(N^2)).
2.下标定位+bfprt算法。
2.1.k–。
2.2.定位下标i1和i2。
i1=k/N。
i2=k%N。
2.3.根据bfprt算法求出第i1小和第i2小的数。
时间复杂度:O(N)。
空间复杂度:O(1)。arr数组里的元素顺序会发生变化。
代码用golang编写。代码如下:
package main
import (
"fmt"
"math/rand"
)
func main() {
arr := []int{1, 2, 3}
k := 4
ret := kthMinPair3(arr, k)
fmt.Println(ret)
}
// O(N)的复杂度,你肯定蒙了
func kthMinPair3(arr []int, k int) []int {
N := len(arr)
if k > N*N {
return nil
}
// 在无序数组中,找到第K小的数,返回值
// 第K小,以1作为开始
fristNum := getMinKth(arr, (k-1)/N)
// 第1维数字
lessFristNumSize := 0
fristNumSize := 0
for i := 0; i < N; i++ {
if arr[i] < fristNum {
lessFristNumSize++
}
if arr[i] == fristNum {
fristNumSize++
}
}
rest := k - (lessFristNumSize * N)
return []int{fristNum, getMinKth(arr, (rest-1)/fristNumSize)}
}
// 改写快排,时间复杂度O(N)
// 在无序数组arr中,找到,如果排序的话,arr[index]的数是什么?
func getMinKth(arr []int, index int) int {
L := 0
R := len(arr) - 1
pivot := 0
var range2 []int
for L < R {
pivot = arr[L+rand.Intn(R-L+1)]
range2 = partition(arr, L, R, pivot)
if index < range2[0] {
R = range2[0] - 1
} else if index > range2[1] {
L = range2[1] + 1
} else {
return pivot
}
}
return arr[L]
}
func partition(arr []int, L int, R int, pivot int) []int {
less := L - 1
more := R + 1
cur := L
for cur < more {
if arr[cur] < pivot {
less++
arr[less], arr[cur] = arr[cur], arr[less]
cur++
} else if arr[cur] > pivot {
arr[cur], arr[more] = arr[more], arr[cur]
more--
} else {
cur++
}
}
return []int{less + 1, more - 1}
}
执行结果如下:
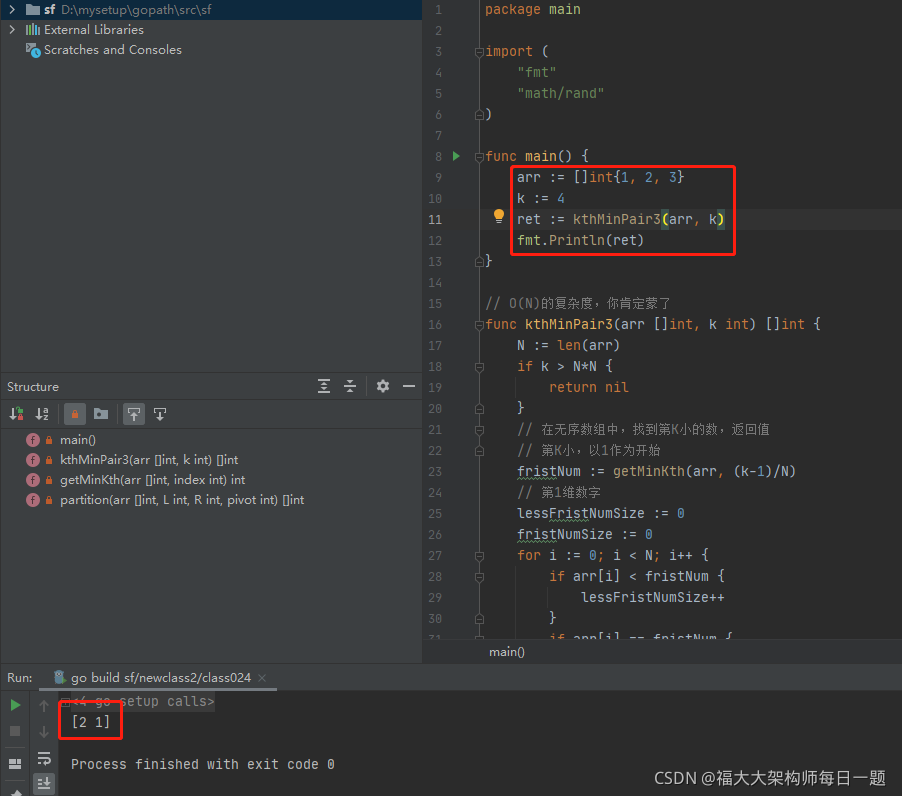
2021-08-26:长度为N的数组arr,一定可以组成N^2个数字对。例如arr = [3,1,2],数字对有(3,3) (3,1) (3,2) (1,3) (1,1) (1,2) (2,3) (2的更多相关文章
- 2021.08.09 P4868 Preprefix sum(树状数组)
2021.08.09 P4868 Preprefix sum(树状数组) P4868 Preprefix sum - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 题意: 前缀和(pr ...
- 2021.08.09 P6225 抑或橙子(树状数组)
2021.08.09 P6225 抑或橙子(树状数组) 重点: 1.异或用法 题意: Janez 喜欢橙子!他制造了一个橙子扫描仪,但是这个扫描仪对于扫描的每个橙子的图像只能输出一个 3232 位整数 ...
- 2021.08.30 前缀函数和KMP
2021.08.30 前缀函数和KMP KMP算法详解-彻底清楚了(转载+部分原创) - sofu6 - 博客园 (cnblogs.com) KMP算法next数组的一种理解思路 - 挠到头秃 - 博 ...
- 2021.08.06 P4392 Sound静音问题(ST表)
2021.08.06 P4392 Sound静音问题(ST表) [P4392 BOI2007]Sound 静音问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 题意: 序列a,求 ...
- GNU C的定义长度为0的数组
在标准C和C++中,长度为0的数组是被禁止使用的.不过在GNU C中,存在一个非常奇怪的用法,那就是长度为0的数组,比如Array[0];很多人可能觉得不可思议,长度为0的数组是没有什么意义的,不过在 ...
- 不用循环,、es6创建一个长度为100的数组
问题描述:在不使用循环的条件下,如何创建一个长度为100的数组,并且数组的每一个元素是该元素的下标? 结果为: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 1 ...
- 前端面试题:不使用loop循环,创建一个长度为100的数组,并且每个元素的值等于它的下标,,怎么实现好?
昨天,看这道题,脑子锈住了,就是没有思路,没看明白是什么意思?⊙﹏⊙|∣今天早上起床,想到需要思考一下这个问题. 当然,我没想明白为什么要这样做?(创建一个长度为100的数组,并且每个元素的值等于它的 ...
- 2021.08.09 P6037 Ryoku的探索(基环树)
2021.08.09 P6037 Ryoku的探索(基环树) P6037 Ryoku 的探索 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 重点: 1.树的性质 2.基环树的性质 ...
- 2021.08.05 P5357 康托展开模板(康托展开)
2021.08.05 P5357 康托展开模板(康托展开) P5367 [模板]康托展开 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 重点: 1.康托展开 算法学习笔记(56): ...
- 2021.07.26 P1022 计算器的改良(字符串)
2021.07.26 P1022 计算器的改良(字符串) 改进: 如果是我出题,我一定把未知数设为ab.buh.bluesky之类的长度不只是1的字符串! 题意: 一个一元一次方程,求解. 分析: 1 ...
随机推荐
- Azure DevOps - 团队成员有权限却无法看到 Azure Repo
我们需要进入Organization Settings, 在Users中找到相关的用户,确认用户Access Level是否为stakeholder. 点击最右侧三个点,Change Acce ...
- Checkmk监控工具使用手册
其实用法Checkmk官网文档很全面:https://docs.checkmk.com/latest/en/intro_setup.html 顺着beginner's guide章节看完基本就能上手, ...
- Spring源码分析之getBean
一.前言 spring作为JAVAEE最核心的框架,是每一个java开发者所必须掌握的,非常重要,本篇从一个简单例子入手,由浅入深的分析spring创建bean的全过程,目标在于彻底搞懂spring原 ...
- python pandas库总结-数据分析和操作工具
参考:https://pandas.pydata.org/ Input/output相关函数 pandas.read_excel-将Excel文件读入pandas数据框 支持读取xls, xlsx, ...
- 论文解读(ToAlign)《ToAlign: Task-oriented Alignment for Unsupervised Domain Adaptation》
论文信息 论文标题:ToAlign: Task-oriented Alignment for Unsupervised Domain Adaptation论文作者:Guoqiang Wei, Cuil ...
- 单机Linux下搭建MongoDB副本集-三节点
前言说明 Linux下安装MongoDB副本集我基本上是一次搭建,几百年不再碰,也记不住具体的命令,偶尔需要搭建都是直接网上找的教程. 有些教程很精简,有些又版本不一样,所以索性我整合下别人的教程,把 ...
- 灵感宝盒新增「线上云展会」产品,「直播观赏联动」等你共建丨RTE NG-Lab 双周报
前言 哈喽各位开发者,「RTE NG-Lab 双周报」如期而至! 近两周,我们更新了一些新的实时互动场景和产品,也举办了代码实验室的第一次线下活动,与大家一起体验了声网最新的 4.0 SDK. 灵感宝 ...
- java网络编程--2 IP,端口,通信协议,TCP/UDP对比
java网络编程--2 IP,端口,通信协议,TCP/UDP对比 1.3.IP ip地址:InetAddress 唯一定位一台网络上的计算机 127.0.0.1 :本机localhost IP地址的分 ...
- SpringBoot——配置嵌入式 Servlet容器
更多内容,前往 IT-BLOG 一.如何定制和修改Servlet容器的相关配置 前言:SpringBoot 在Web 环境下,默认使用的是 Tomact 作为嵌入式的 Servlet容器: [1]修 ...
- Linux Redhat ens33不显示IP问题
[第一步]:查看系统网卡设备 : ip addr show
