P2365 任务安排 batch 动态规划

batch

★☆   输入文件：batch.in   输出文件：batch.out   简单对比
时间限制：1 s   内存限制：128 MB

题目描述

N个任务排成一个序列在一台机器上等待完成（顺序不得改变），这N个任务被分成若干批，每批包含相邻的若干任务。从时刻0开始，这些任务被分批加工，第i个任务单独完成所需的时间是T_i。在每批任务开始前，机器需要启动时间S，而完成这批任务所需的时间是各个任务需要时间的总和（同一批任务将在同一时刻完成）。每个任务的费用是它的完成时刻乘以一个费用系数F_i。请确定一个分组方案，使得总费用最小。

例如：S=1；T={1,3,4,2,1}；F={3,2,3,3,4}。如果分组方案是{1,2}、{3}、{4,5}，则完成时间分别为{5,5,10,14,14}，费用C={15,10,30,42,56}，总费用就是153。

输入格式

第一行是N(1<=N<=5000)。

第二行是S(0<=S<=50)。

下面N行每行有一对数，分别为T_i和F_i，均为不大于100的正整数，表示第i个任务单独完成所需的时间是T_i及其费用系数F_i。

输出格式

一个数，最小的总费用。

输入样例

5
1
1 3
3 2
4 3
2 3

1 4

输出样例

153

额  哇哇哇  dp写挂了 QAQ

正解1

f[i]   前i个任务的最优结果

f[i]=min{f[j] +sumt[i]*(sumc[i]-sumc[j])+S*(sumc[n]-sumc[j])}

好东西呢 唉 QAQ

详细题解如下：

暴力方法

由于每一批任务连续，所以预处理出两个前缀和数组：

sumt[i] 表示 执行前i个任务所需要的时间 ， 即t[1]+t[2]+...+t[n]

sumc[i] 表示 不乘时间时，执行前i个任务所需要的费用 ， 即c[1]+c[2]+...+c[n]

dp子状态：

dp[i][j] 表示 前i个任务分成j批所需要的最小费用。

于是可以由dp[k][j-1]推出dp[i][j]：

dp[i][j]=min{dp[k][j-1]+(s*j+sumt[i])*(sumc[i]-sumc[k])}

时间复杂度O(n^3)，

空间复杂度O(n^2)。

略微优化

暴力方法的dp子状态空间是二维的，由于N <= 10000 ，所以考虑将二维状态降到一维。

将第一维去掉的想法不太实际，故考虑将第二维去掉。

首先思考所有任务都放到同一批中，观察每个任务需要等待S时间的次数：

任务编号 1  2  3  ...  n

等待次数 1  1  1  ...  1

当将1~pos1分成一个区间时，每个任务需要等待的次数变为：

任务编号 1  2  3  ...  pos1  pos1+1  ...  n

等待次数 1  1  1  ...   1      2     ...  2

（如果仍然看不出来，可以再分几次找找规律）

观察等待次数：每次多分出一个区间，区间左端点到n都需要多等待一次S时间。

故可以推出一个新的方程：

dp[i]=min{dp[j]+sumt[i]*(sumc[i]-sumc[j]+s*(sumc[n]-sumc[j]))

dp[i]并不只是前i个的时间  还要加上对后面的影响

上面其实就已经AC了  （但是老师的本意是要让我们写斜率优化）

斜率优化

当每次求dp[i]时，分别整理i，j的信息，把原来的方程进行玄学变形（移项）：

dp[i]=min{dp[j]-(s+sumt[i])*sumc[j]}+sumt[i]*sumc[i[]+s*sumc[n]

去掉min函数，把dp[j]和sumc[j]看作变量，整理出dp[j]关于sumc[j]的一次函数（重要！）：

dp[j]=(s+sumt[i]) * sumc[j] + (dp[i]-sumt[i]*sumc[i]-s*sumc[n])

y  =    k       *    x    +                 b

其中sumc[j]是自变量，dp[j]是因变量，s+sumt[i]是斜率，后面一串为截距。

建立一个平面直角坐标系：

每个决策j的二元组(sumc[j] , dp[j])表示坐标系中的点。

当前状态dp[i]表示直线的截距（且这条直线斜率为s+sumt[i]）。

令直线过每个点可以得到解出截距，使截距最小的就是最优决策。

如图：

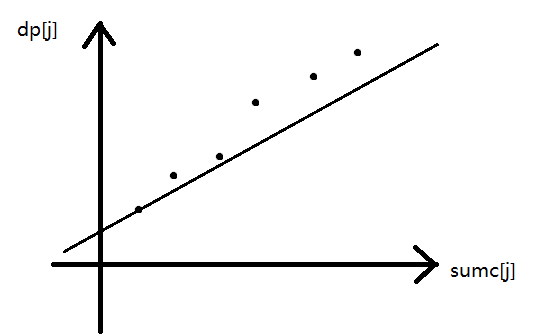
讨论三个决策点j1,j2,j3（j1<j2<j3）对应的坐标系中的点：

第一种情况：上凸。用眼睛观察（hhh）可知，j2此时不可能成为最佳决策点，故放弃。

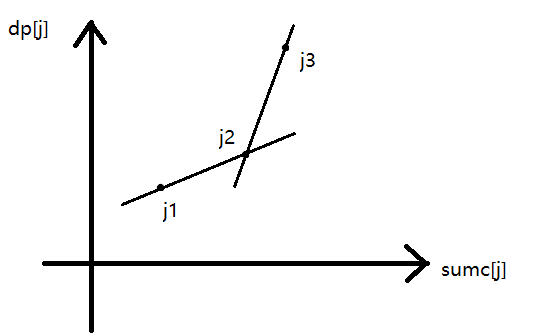
第二种情况：下凹。此时j2有可能成为最佳决策点。

最后把所有可能成为最佳决策点的j处理出来，即维护一个相邻点斜率单调递增的“凸壳”。

其中最佳决策点左端斜率<s+sum[i]，右端斜率>s+sum[i]（可以证明这样的点只有一个）。

又因为s+sumt[i]是单调递增的，所以可以用单调队列找第一个右端斜率>s+sum[i]的点。

总时间复杂度：循环递推O(n)+单调队列O(n)=O(n)。

空间复杂度：一维状态O(n)。

#include <stdio.h>
typedef long long ll;
typedef double db;
const int N=1e6+;
int n,S,s[N],t[N],q[N],head,tail;
ll dp[N],val[N];
db k(int j,int k){return (db)(val[j]-val[k])/(s[j]-s[k]);}
int main()
{
    freopen("batch.in","r",stdin);
    freopen("batch.out","w",stdout);
    scanf("%d%d",&n,&S);
    for (int i=;i<=n;i++){
        scanf("%d%d",&t[i],&s[i]);
        t[i]+=t[i-];
        s[i]+=s[i-];
    }
    q[head=tail=]=;
    for (int i=;i<=n;i++){
        for (;head<tail&&k(q[head],q[head+])<S+t[i];head++);
        int j=q[head];
        dp[i]=dp[j]+ll(s[n]-s[j])*(S+t[i]-t[j]);
        val[i]=dp[i]+(ll)s[i]*t[i]-(ll)s[n]*t[i];
        for (;head<tail&&k(q[tail-],q[tail])>k(q[tail],i);tail--);
        q[++tail]=i;
    }
    printf("%lld\n",dp[n]);
    return ;
}

N^2暴力AC！

#include<bits/stdc++.h>
#define maxn 5005
using namespace std;
int t[maxn],f[maxn],sumt[maxn],sumf[maxn],dp[maxn];
int main(){
//    freopen("batch.in","r",stdin);freopen("batch.out","w",stdout);
    int n,s;scanf("%d%d",&n,&s);
    for(int i=;i<=n;i++) scanf("%d%d",&t[i],&f[i]);
    for(int i=;i<=n;i++) sumt[i]=sumt[i-]+t[i],sumf[i]=sumf[i-]+f[i];
    memset(dp,0x3f,sizeof(dp));
//    dp[1]=t[1]*f[1]+s*(sumf[n]-sumf[1]);
    dp[]=;
    for(int i=;i<=n;i++)
        for(int j=;j<i;j++)
            dp[i]=min(dp[i],dp[j]+sumt[i]*(sumf[i]-sumf[j])+s*(sumf[n]-sumf[j]));
    printf("%d",dp[n]);
    //f[i]=min{f[j] +sumt[i]*(sumc[i]-sumc[j])+S*(sumc[n]-sumc[j])}
    return ;
}