如何选择kmeans中的k值——肘部法则–Elbow Method和轮廓系数–Silhouette Coefficient

肘部法则–Elbow Method

我们知道k-means是以最小化样本与质点平方误差作为目标函数，将每个簇的质点与簇内样本点的平方距离误差和称为畸变程度(distortions)，那么，对于一个簇，它的畸变程度越低，代表簇内成员越紧密，畸变程度越高，代表簇内结构越松散。 畸变程度会随着类别的增加而降低，但对于有一定区分度的数据，在达到某个临界点时畸变程度会得到极大改善，之后缓慢下降，这个临界点就可以考虑为聚类性能较好的点。

import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

df_features = pd.read_csv(r'11111111.csv',encoding='gbk') # 读入数据
#print(df_features)
'利用SSE选择k'
SSE = []  # 存放每次结果的误差平方和
for k in range(1,9):
    estimator = KMeans(n_clusters=k)  # 构造聚类器
    estimator.fit(df_features[['','','','','','','','','','','','','','','','','','','','','','','','','','','','','','','','','']])
    SSE.append(estimator.inertia_) # estimator.inertia_获取聚类准则的总和
X = range(1,9)
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(X,SSE,'o-')
plt.show()

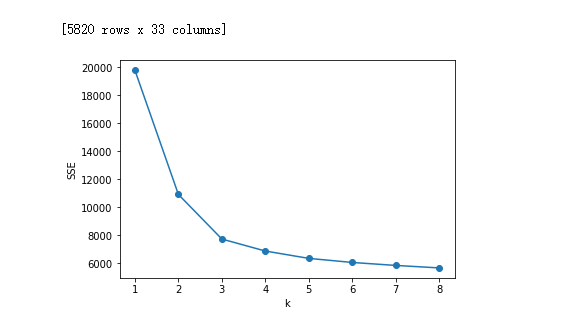
如上图所示，在k=xxxxxx时，畸变程度(y值)得到大幅改善，可以考虑选取k=xxxxx作为聚类数量 显然，肘部对于的k值为xxxxxx(曲率最高)，故对于这个数据集的聚类而言，最佳聚类数应该选xxxxxxxx。

轮廓系数–Silhouette Coefficient

对于一个聚类任务，我们希望得到的簇中，簇内尽量紧密，簇间尽量远离，轮廓系数便是类的密集与分散程度的评价指标，公式表达如下： s=b−amax(a,b)s=b−amax(a,b) 其中a代表同簇样本到彼此间距离的均值，b代表样本到除自身所在簇外的最近簇的样本的均值，s取值在[-1, 1]之间。 如果s接近1，代表样本所在簇合理，若s接近-1代表s更应该分到其他簇中。

判断： 轮廓系数范围在[-1,1]之间。该值越大，越合理。 si接近1，则说明样本i聚类合理； si接近-1，则说明样本i更应该分类到另外的簇； 若si 近似为0，则说明样本i在两个簇的边界上。 所有样本的s i 的均值称为聚类结果的轮廓系数，是该聚类是否合理、有效的度量。 使用轮廓系数(silhouette coefficient)来确定，选择使系数较大所对应的k值

sklearn.metrics.silhouette_score sklearn中有对应的求轮廓系数的API

import numpy as np
from sklearn.cluster import KMeans
from pylab import *
import codecs
import matplotlib.pyplot as plt
from sklearn.metrics import calinski_harabaz_score
import pandas as pd
from numpy.random import random
from sklearn import preprocessing
from sklearn import metrics
import operator  

data = []
labels = []
number1=10
with codecs.open("red_nopca_nolabel.txt", "r") as f:
    for line in f.readlines():
        line1=line.strip()
        line2 = line1.split(',')
        x2 = []
        for i in range(0,number1):
            x1=line2[i]
            x2.append(float(x1))
        data.append(x2)
        x2 = []
        #label = line2[number1-1]
        #labels.append(float(label))
datas = np.array(data)
'''
kmeans_model = KMeans(n_clusters=3, random_state=1).fit(datas)
labels = kmeans_model.labels_
a = metrics.silhouette_score(datas, labels, metric='euclidean')
print(a)
'''
silhouette_all=[]

for k in range(2,25):
    kmeans_model = KMeans(n_clusters=k, random_state=1).fit(datas)
    labels = kmeans_model.labels_
    a = metrics.silhouette_score(datas, labels, metric='euclidean')
    silhouette_all.append(a)
    #print(a)
    print('这个是k={}次时的轮廓系数：'.format(k),a)

dic={}             #存放所有的互信息的键值对
mi_num=2
for i in silhouette_all:
    dic['k={}时轮廓系数'.format(mi_num)]='{}'.format(i)
    mi_num=mi_num+1
#print(dic)
rankdata=sorted(dic.items(),key=operator.itemgetter(1),reverse=True)
print(rankdata)

实验结果部分插图