C语言程序设计100例之（28）：直线蛇形阵

例28 直线蛇形阵

问题描述

编写程序，将自然数1、2、…、N²按蛇形方式逐个顺序存入N阶方阵。例如，当N=3和N=4时的直线蛇形阵如下图1所示。

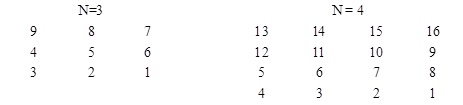
图1 直线蛇形阵

输入格式

一个正整数n（1≤n≤20）。

输出格式

N阶满足要求的直线蛇形方阵。输出时共n行，每行n个数，每个数占4列。

输入样例

输出样例

13 14 15 16

12 11 10 9

5 6 7 8

4 3 2 1

（1）编程思路。

从图1可以看出，直线蛇形阵的构造是从最底行（row=N-1）向最顶行（row=0）进行的。每行的填写在两种方式间切换，一种方式是从右到左顺序（即for(j=n-1;j>=0;j--) ）依次递增1填写，称为方式1；另一种方式是从左到右顺序（即for(j=0;j<=n-1;j++) ）依次递增1填写，称为方式2。

程序中定义一个变量k来标志这两种方式，k初始值为0，表示采用方式1，当前行按方式1填写完后，改变k的值，使其等于1，表示采用方式2，当前行按方式2填写完后，再改变k的值，使其等于0。

（2）源程序。

#include<stdio.h>

int main()

{

int a[20][20]={0},n;

scanf("%d",&n);

int i,j,k=0,t=1;

for(i=n-1;i>=0;i--) // 遍历行

{

if(k==0) // 从右到左顺序依次递增1存数组元素

{

for(j=n-1;j>=0;j--)

a[i][j]=t++;

k=1;

}

else // 从左到右顺序依次递增1存数组元素

{

for(j=0;j<=n-1;j++)

a[i][j]=t++;

k=0;

}

for (i=0;i<n;i++)

{

for (j=0;j<n;j++)

printf("%4d",a[i][j]);

printf("\n");

}

return 0;

}

习题28

28-1 斜线蛇形阵

问题描述

编写程序，将自然数1、2、…、N²按蛇形方式逐个顺序存入N阶方阵。例如，当N=3和N=4时的方阵如下图2所示。

图2 斜线蛇形阵

输入格式

一个正整数n（1≤n≤20）。

输出格式

N阶满足要求的斜线蛇形方阵。输出时共n行，每行n个数，每个数占4列。

输入样例

输出样例

15 16 22 23 25

7 14 17 21 24

6 8 13 18 20

2 5 9 12 19

1 3 4 10 11

（1）编程思路。

观察图2所示的斜线蛇形阵可知，方阵在逐个填数构造的过程中，是沿两种斜线进行的，一种是斜向下，一种是斜向上，如图3（a）所示。

设当前已填入数字的位置的行号为row（row在0~n-1之间），列号为col（col也在0~n-1之间）。若按斜向下填写，则下一位置为row++、col++ ；若按斜向上填写，则下一位置为row--、col--。由于下一位置可能超出方阵的边界，因此有时需要调整。调整有4种情况，下面分别进行说明。

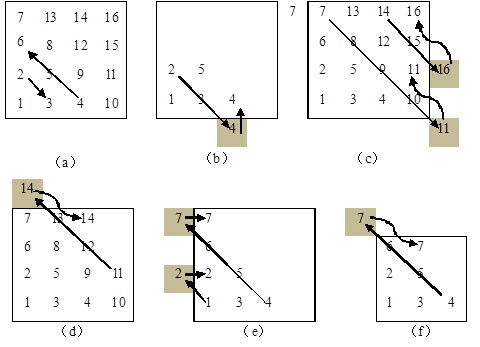
图3 斜线蛇形阵的构造示意图

斜向下填写时，会出现两种情况：

1）超过了底行的位置（即row==n），如图3（b）所示，3填写好后，下一个数4的计算位置越界了，此时进行调整，方法为列col不变，row减1（即 row--）。

2）超过最右列的位置（即col==n），如图3（c）所示，15填写好后，下一个数16的计算位置越界了，此时进行调整，方法为col--、row=row-2。

一种特例，10填写好后，下一个数11的计算位置，行和列都越界了，但处理方法同列越界，因此在程序中应先处理col==n的情况，再处理row==n的情况。这样对于这种特例，由于处理了col==n后，row减了2，不会越界，因此不会再处理row==n的情况。

斜向上填写时，也会出现两种情况：

1）超过了首行的位置（即row==-1），如图3（d）所示，13填写好后，下一个数14的计算位置越界了，此时进行调整，方法为row++、col=col-2。

2）超过最左列的位置（即col==-1），如图3（e）所示，6填写好后，下一个数7的计算位置越界了，此时进行调整，方法为row不变、列号加1（即col++）。

一种特例，在如图3（f）所示的3阶方阵中，6填写好后，下一个数7的计算位置，行和列都越界了，其处理方法同行越界，因此在程序中应先处理row==-1的情况，再处理col==-1的情况。这样对于这种特例，由于处理了row==-1后，col加了2，不会越界，因此不会再处理col==-1的情况。

每次进行越界调整填数后，填数的方向也会发生变化。因此，可设置一个变量up，当up=1时，表示斜向上填数；up=0时，表示斜向下填数。

初始化时，令up=1、row=n-1、col=0、 num=1；在当前位置填上1（即a[row][col]=1），之后进行循环，直到n*n个数填写完毕。循环中，总是先按up的方向，确定下一个位置，然后填上相应的数。例如，1向上到2，越界，调整即可，如图3（e）所示。

（2）源程序。

#include<stdio.h>

int main()

{

int a[20][20]={0},n;

scanf("%d",&n);

int up=1;

int row=n-1;

int col=0;

int num=1;

a[row][col]=num++;

while (num<=n*n)

{

if (up) { row--; col--;}

else { row++; col++;}

if (row==-1) // 超过首行的位置

{ row++; col=col+2; up=1-up; }

if (col==n) // 超过最右列的位置

{ row=row-2; col--; up=1-up; }

if (row==n) // 超过底行的位置

{ row--; up=1-up; }

if (col==-1) // 超过最左列的位置

{ col++; up=1-up; }

a[row][col]=num++;

}

for (int i=0;i<n;i++)

{

for (int j=0;j<n;j++)

printf("%4d",a[i][j]);

printf("\n");

}

return 0;

}

若将程序中的up的初始值设定为0，即开始斜向下填写。重新编译并执行以上程序，则得到如下所示的结果。

11 19 20 24 25

10 12 18 21 23

4 9 13 17 22

3 5 8 14 16

1 2 6 7 15

28-2 对称方阵

问题描述

图4所示为两个7阶对称方阵，形象起见，可将（a）方阵称为环形对称方阵，（b）方阵称为三角形对称方阵。

图4 对称方阵

输入格式

两个正整数n（1≤n≤20）和k（k为1或2）。

输出格式

N阶满足要求的对称方阵。若k=1，输出环形对称方阵，k=2，输出三角形对称方阵。输出时共n行，每行n个数，每个数占3列。

输入样例1

5 1

输出样例1

0 1 1 1 0

1 0 2 0 1

1 2 0 2 1

1 0 2 0 1

0 1 1 1 0

输入样例2

7 2

输出样例2

0 1 2 3 2 1 0

1 0 1 2 1 0 1

2 1 0 1 0 1 2

3 2 1 0 1 2 3

2 1 0 1 0 1 2

1 0 1 2 1 0 1

0 1 2 3 2 1 0

（1）编程思路。

1）生成如图4（a）所示的环形对称方阵的方法。

设方阵中元素的行号为row，列号为col。为方便见，row和col均从1开始计。

方阵的主对角线（即row==col）和次对角线（即row+col==n+1）的各元素均赋值“0”。

按两条对角线把方阵可分成上部、左部、右部与下部4个区，如图5所示。

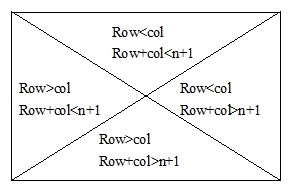
图5 环形对称方阵的四个分区

四个分区的赋值方式为：

上部按行号row赋值，即if (row+col<n+1 && row<col) a[row][col]=row。

下部按表达式n+1-row赋值，即if (row+col>n+1 && row>col) a[row][col]=n+1-row。

左部按列号col赋值，即if (row+col<n+1 && row>col) a[row][col]=col。

右部按表达式n+1-col赋值，即if (row+col>n+1 && row<col) a[row][col]=n+1-col。

2）生成如图4（b）所示的三角形对称方阵的方法。

令m=(n+1)/2，按图6（a）所示分成4个区。

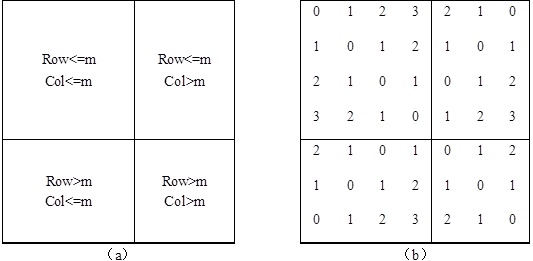
图6 三角形对称方阵的四个分区

仔细分析这个四个分区的元素值与行号、列号的关系，并参照图6（b）所示的7阶对称方阵各元素的值，可归纳出：

左上区（row<=m && col<=m）与右下区（row>m && col>m）参照主对角线赋值：

a[row][col]=abs(row-col) 。

右上区（(row<=m && col>m）与左下区（row>m && col<=m）参照次对角线赋值：

a[row][col]= abs(row+col-n-1)。

（2）源程序。

#include <stdio.h>

#include <math.h>

int main()

{

int n,k,row,col,a[21][21]={0};

scanf("%d%d",&n,&k);

if (k==1)

{

for (row=1; row<=n; row++)

for (col=1; col<=n; col++)

{

if (row==col || row+col==n+1)

a[row][col]=0; // 方阵对角线元素赋值

if (row+col<n+1 && row<col)

a[row][col]=row; // 方阵上部元素赋值

if (row+col<n+1 && row>col)

a[row][col]=col; // 方阵左部元素赋值

if (row+col>n+1 && row>col)

a[row][col]=n+1-row; // 方阵下部元素赋值

if (row+col>n+1 && row<col)

a[row][col]=n+1-col; // 方阵右部元素赋值

}

else

{

int m=(n+1)/2;

for (row=1; row<=n; row++)

for (col=1; col<=n; col++)

{

if ((row<=m && col<=m) || (row>m && col>m))

a[row][col]=abs(row-col); // 方阵左上部与右下部元素赋值

if ((row<=m && col>m) || (row>m && col<=m))

a[row][col]=abs(row+col-n-1); // 方阵右上部与左下部元素赋值

}

for (int i=1;i<=n;i++)

{

for (int j=1;j<=n;j++)

printf("%3d",a[i][j]);

printf("\n");

}

return 0;

}

28-3 螺旋下三角阵

问题描述

编写程序，将自然数1、2、…、（1+N）*N/2按螺旋方式逐个顺序存入N阶下三角矩阵。例如，当N=3和N=4时的矩阵如下图7所示。

图7 螺旋下三角阵

输入格式

一个正整数n（1≤n≤20）。

输出格式

N阶满足要求的螺旋下三角阵。输出时每个数占4列。

输入样例

输出样例

1 2 3 4 5

12 13 14 6

11 15 7

10 8

（1）编程思路

螺旋下三角阵的构造可以看成由向右填充（行号不变、列号加1，即col++）、斜向下填充（row++、col--）和向上填充（行号减1、列号不变，即row--）三个子过程不断交替完成的。

例如，图8所示的3阶螺旋下三角阵可以看成由向右填充（1、2、3），斜向下填充（4、5）和向上填充（6）这3个子过程完成的。4阶螺旋下三角阵可以看成由向右填充（1、2、3、4），斜向下填充（5、6、7）、向上填充（8、9）和向右填充（10）这4个子过程完成的。

n阶螺旋下三角阵可以看成由n个子过程完成，每个子过程为向右填充、斜向下填充和向上填充这三种中的一种，用变量direction来表示，其取值为0、1或2，0表示向右填充，1表示斜向下填充，2表示向上填充。每个子过程结束后，切换填充方向，方式为：

direction=(direction+1)%3;

n个子过程中，第1个子过程填写n个数，第2个子过程填写n-1个数，…，最后一个子过程填写1个数。因此，程序总体写成一个二重循环，描述为：

for (i=n;i>=1;i--)

{

for (j=1;j<=i;j++)

{

按填充方向，填充相应数据

}

direction=(direction+1)%3; // 切换填充方向

}

初始时，注意row=0，col=-1，这样向右col++后，col为0，正好填在第1个位置。

（2）源程序。

#include <stdio.h>

int main()

{

int a[20][20]={0},row,col,i,j,n,num;

int direction=0;

scanf("%d",&n);

row=0; col=-1; num=1;

for (i=n;i>=1;i--)

{

for (j=1;j<=i;j++)

{

switch(direction)

{

case 0:col++;break; // 向右填充

case 1:row++;col--;break; // 斜向下填充

case 2:row--;break; // 向上填充

}

a[row][col]=num++;

}

direction=(direction+1)%3; // 切换填充方向

}

for(row=0;row<n;row++)

{

for(col=0;col<n-row;col++)

printf("%4d",a[row][col]);

printf("\n");

}

return 0;

}