学习JDK1.8集合源码之--TreeMap
1. TreeMap简介
TreeMap继承自AbstractMap，实现了NavigableMap、Cloneable、java.io.Serializable接口。所以TreeMap也是一个key-value结构的Map集合，并且提供了搜索导航及排序功能，能够被克隆以及支持序列化操作。
TreeMap是基于红黑树实现的有序key-value集合，可以对元素进行自动排序，排序的规则可以是自然排序也可以是实现Comparable接口指定排序方式。
由于红黑树的查找、插入和删除的时间复杂度都是O(logn)，所以TreeMap的查找、插入和删除等操作的时间复杂度也都是O(logn)。相比HashMap，TreeMap的优势是能够自动排序，适合在需要排序的场景下使用。HashMap适合在需要快速查找的场景下使用，而LinkedHashMap适合在即需要快速查找也需要排序的场景下使用。
TreeMap是非线程安全的，若有线程安全问题建议使用ConcurrentSkipListMap代替。它的iterator方法返回的迭代器是fail-fast的。
2. 红黑树简介
在看TreeMap的具体实现之前，必须要了解一下红黑树的概念，摘自百度百科（https://baike.baidu.com/item/%E7%BA%A2%E9%BB%91%E6%A0%91/2413209?fr=aladdin）。红黑树是一种近似平衡的二叉树，因为它保证了从根到叶子的最长的可能路径不多于最短的可能路径的两倍长，而这个保证是根据以下约束条件来实现的：
1. 节点是红色或黑色。
2. 根节点是黑色。
3. 每个叶子节点（NIL）是黑色。(不知道为什么百度百科里为什么没有这个性质，java里NIL节点就是Null节点)
4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
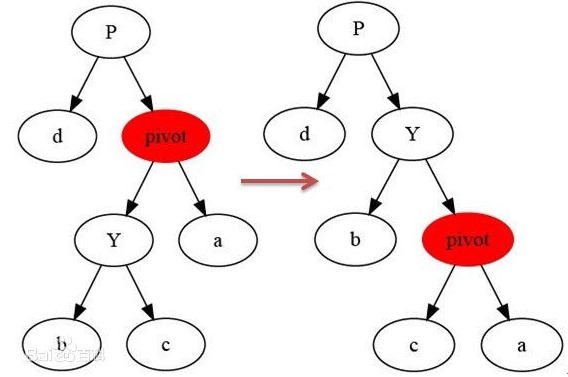
//左旋，实际就是把p节点变成其右子树r的左子树，r的左子树变成p的右子树
private void rotateLeft(Entry<K,V> p) {
//以p为轴心进行左旋，故p不能为空
if (p != null) {
//取p的右子树r(进行左旋的节点一定是有子节点的)
Entry<K,V> r = p.right;
//先将r的左子树作为p的右子树
p.right = r.left;
//如果r的左子树不为空，则将r的左子树的父节点设为p
if (r.left != null)
r.left.parent = p;
//将p的父节点设为r的父节点
r.parent = p.parent;
//如果p的父节点是空的，将r设为root节点
if (p.parent == null)
root = r;
//如果p是左子树，则将r设为p的父节点的左子树
else if (p.parent.left == p)
p.parent.left = r;
//如果p是右子树，则将r设为p的父节点的右子树
else
p.parent.right = r;
//将p设为r的左子树
r.left = p;
//将p设为r的父节点
p.parent = r;
}
} //右旋，实际上就是把p设为其左子树l的右子树，并把l的右子树设为p的左子树
private void rotateRight(Entry<K,V> p) {
//以p为轴心进行右旋，故p不能为空
if (p != null) {
//取p的左子树l
Entry<K,V> l = p.left;
//将l的右子树设为p的左子树
p.left = l.right;
//如果l的右子树不为空，则将l额右子树的父节点设为p
if (l.right != null) l.right.parent = p;
//将p的父节点设为l的父节点
l.parent = p.parent;
//如果p的父节点为空，将l设为root
if (p.parent == null)
root = l;
//如果p是右子树，则将l设为p的父节点的右子树
else if (p.parent.right == p)
p.parent.right = l;
//如果p是左子树，则将l设为p的父节点的左子树
else p.parent.left = l;
//将p设为r的右子树
l.right = p;
//将l设为p的父节点
p.parent = l;
}
}
3. TreeMap实现
1. 核心属性
//比较器
private final Comparator<? super K> comparator;
//根节点
private transient Entry<K,V> root;
//TreeMap大小
private transient int size = 0;
//修改次数，用于fail-fast机制
private transient int modCount = 0;
//TreeMap中元素的set结合
private transient EntrySet entrySet;
//有序的key集合
private transient KeySet<K> navigableKeySet;
//红色
private static final boolean RED = false;
//黑色
private static final boolean BLACK = true;//红黑树节点
static final class Entry<K,V> implements Map.Entry<K,V> {
K key;
V value;
//左孩子
Entry<K,V> left;
//右孩子
Entry<K,V> right;
//父节点
Entry<K,V> parent;
//红黑树的颜色
boolean color = BLACK; Entry(K key, V value, Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
... }
2. 构造函数
TreeMap的构造函数都比较简单，围绕着排序方式进行构造，传入比较器则按照比较器规则排序，否则使用自然排序方式。
//无参构造，使用自然排序方式
public TreeMap() {
comparator = null;
} //指定比较器，按照比较器规则进行排序
public TreeMap(Comparator<? super K> comparator) {
this.comparator = comparator;
} //将m中所有元素放入TreeMap，使用自然排序方式
public TreeMap(Map<? extends K, ? extends V> m) {
comparator = null;
putAll(m);
} //传入一个包含比较器的m，使用m的比较器，并将m中的元素插入TreeMap
public TreeMap(SortedMap<K, ? extends V> m) {
comparator = m.comparator();
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
}
3. 获取节点
因为TreeMap是基于红黑树实现的，而红黑树是一种二分查找树，所以获取元素时的算法也是一种二分查找，从根节点root开始通过比较大小依次寻找与目标key比较接近的值，直到找到目标key或叶子节点为止。而比较的方式则是自然排序方式或指定比较器方式。
//根据key获取Entry实体
final Entry<K,V> getEntry(Object key) {
//如果比较器不为空，按照比较器的规则去查找
if (comparator != null)
return getEntryUsingComparator(key);
//如果key为空则抛出空指针异常，否则按照自然排序方式查找
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
//将key转为一个Comparable对象k
Comparable<? super K> k = (Comparable<? super K>) key;
//取TreeMap的根节点赋值给p
Entry<K,V> p = root;
while (p != null) {
//将p的key与目标key进行比较
int cmp = k.compareTo(p.key);
//如果k比较小，则继续和p的左子树的key进行比较
if (cmp < 0)
p = p.left;
//如果k比较大，则继续和p的右子树的key进行比较
else if (cmp > 0)
p = p.right;
//如果p和p的key相同，则将p返回
else
return p;
}
//没有找到相同的key，返回null
return null;
} //使用指定比较器根据key获取Entry实体
final Entry<K,V> getEntryUsingComparator(Object key) {
@SuppresWarnings("unchecked")
//将key转为泛型类型
K k = (K) key;
//获取指定的比较器
Comparator<? super K> cpr = comparator;
if (cpr != null) {
//取TreeMap的根节点赋值给p
Entry<K,V> p = root;
while (p != null) {
//将p的key与目标key进行比较
int cmp = cpr.compare(k, p.key);
//如果k比较小，则继续和p的左子树的key进行比较
if (cmp < 0)
p = p.left;
//如果k比较大，则继续和p的右子树的key进行比较
else if (cmp > 0)
p = p.right;
//如果p和p的key相同，则将p返回
else
return p;
}
}
//没有找到相同的key，返回null
return null;
}
4. 添加节点
添加元素时也会先通过比较进行类似查找的操作，如果查找到与插入元素key相同到的节点，则直接把该节点的值替换。否则一直找到与添加元素key值最接近的叶子节点作为parent，如果添加的key较大，则设为parent的右子节点，若key较小则设为parent的左子节点。添加完成之后，如果parent节点时黑色则无需调整树的结构，如果是红色则违背了红黑树的规则：红色节点的子节点都是黑色，这时就需要调整红黑树的结构。
插入分为8种情况（插入结点都为红色，简化了插入时的调整工作）：
1. 红黑树为空：直接把插入节点设为root节点，设为黑色；
2. 插入节点key已存在：直接将该节点value替换；
3. 插入节点的父节点是黑色：直接插入节点，设为红色，无需调整树结构；
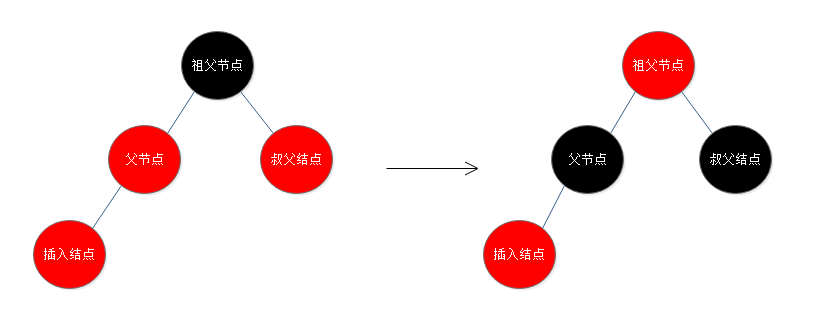
4. 插入节点的父节点是红色，叔父节点为红色：这时因为父节点是红色的，所以肯定不是root节点，所以一定存在黑色的祖父节点，插入节点是红色违背了红黑树规则4，所以将父节点及叔父节点设为黑色，祖父节点设为红色，如果这时还不平衡就继续从父节点开始进行调整；
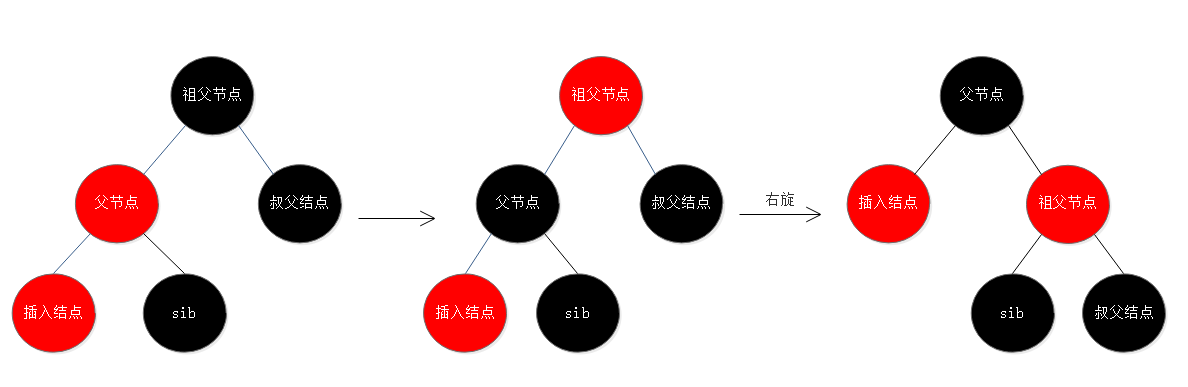
5. 插入节点的父节点是红色，父节点是祖父节点的左子节点，叔父节点为黑色，插入节点为父节点的左子节点：将父节点设为黑色，祖父节点设为红色，此时插入节点所在分支保持平衡，但叔父节点所在分支却少了一个黑色节点，故以祖父节点为轴心进行一次右旋操作，右旋后原祖父节点变为父节点的右子节点，父节点变为原叔父节点的祖父节点，如此原叔父节点所在的分支上多了父节点这一黑色节点保持了平衡；
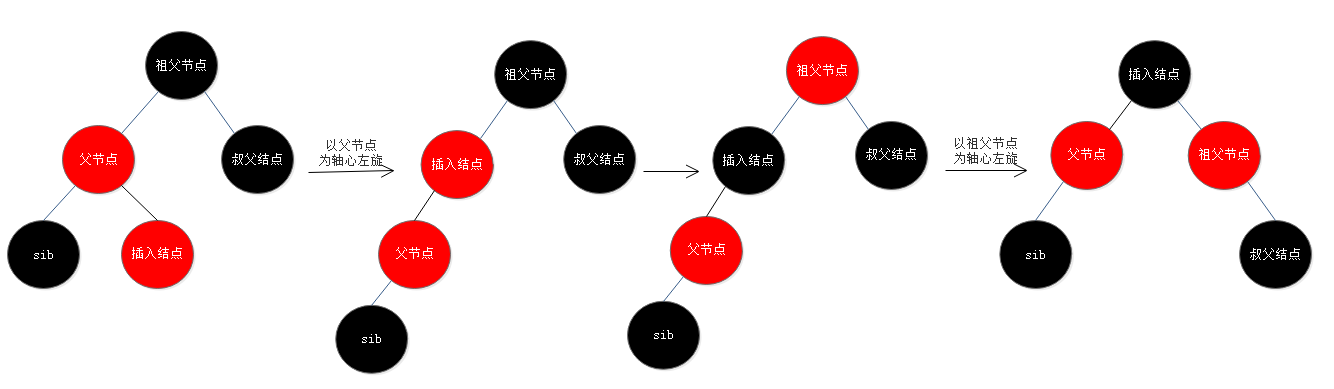
6. 插入节点的父节点是红色，父节点是祖父节点的左子节点，叔父节点为黑色，插入节点为父节点的右子节点：以父节点为轴心进行左旋，左旋后父节点变为插入节点的左子节点，这时转为了第5条一样的操作；
7. 插入节点的父节点是红色，父节点是祖父节点的右子节点，叔父节点为黑色，插入节点为父节点的右子节点：将父节点设为黑色，祖父节点设为红色，此时插入节点所在分保持平衡，但叔父节点所在分支少了一个黑色节点，故以祖父节点进行左旋操作，左旋后原祖父节点变为父节点的左子节点，父节点变原叔父节点的祖父节点，如此原叔父节点所在的分支上多了父节点这一黑色节点保持了平衡；
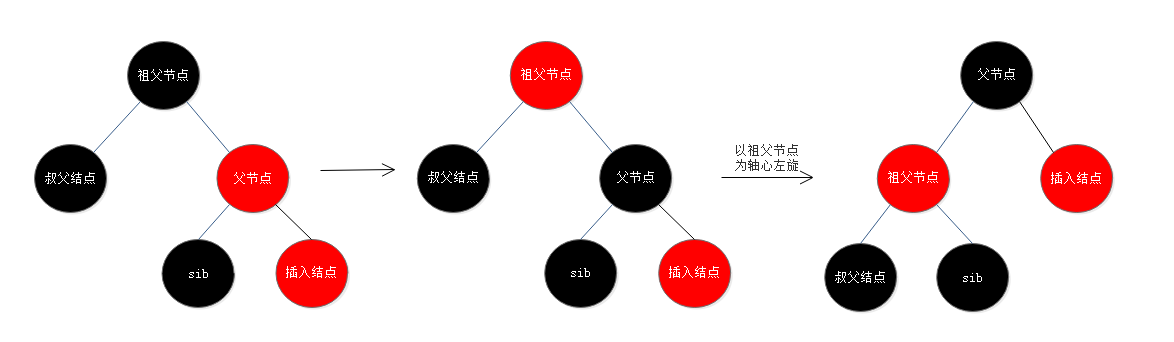
8. 插入节点的父节点是红色，父节点是祖父节点的右子节点，叔父节点为黑色，插入节点为父节点的左子节点：以父节点为轴心进行右旋，右旋后父节点变为插入节点的右子节点，这时转为了第5条一样的操作；
//向TreeMap中添加一个key-value键值对
public V put(K key, V value) {
//取TreeMap的根节点赋值给t
Entry<K,V> t = root;
//如果根节点为空，则直接把key-value放在根节点
if (t == null) {
compare(key, key); // type (and possibly null) check root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
//声明一个cmp变量，用来存储比较结果
int cmp;
//声明一个parent变量，用来存储新增节点的父节点
Entry<K,V> parent;
//取指定的比较器
Comparator<? super K> cpr = comparator;
//如果比较器不为空，按照比较器的规则
if (cpr != null) {
do {
//从根节点开始遍历树，通过比较找到插入节点的父节点
parent = t;
//把当前节点与插节点的key进行比较
cmp = cpr.compare(key, t.key);
//如果插入节点的key比当前节点的key小，则继续与当前节点的左子树key比较
if (cmp < 0)
t = t.left;
//如果插入节点的key比当前节点的key大，则继续与当前节点的右子树key比较
else if (cmp > 0)
t = t.right;
//如果比较结果相同，直接把当前节点的值设为目标值并返回
else
return t.setValue(value);
} while (t != null);
}
//否则按照自然排序方式
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
//取默认比较器
Comparable<? super K> k = (Comparable<? super K>) key;
do {
//从根节点开始遍历树，通过比较找到插入节点的父节点
parent = t;
//把当前节点与插节点的key进行比较
cmp = k.compareTo(t.key);
//如果插入节点的key比当前节点的key小，则继续与当前节点的左子树key比较
if (cmp < 0)
t = t.left;
//如果插入节点的key比当前节点的key大，则继续与当前节点的右子树key比较
else if (cmp > 0)
t = t.right;
//如果比较结果相同，直接把当前节点的值设为目标值并返回
else
return t.setValue(value);
} while (t != null);
}
//新建节点
Entry<K,V> e = new Entry<>(key, value, parent);
//如果key比父节点的key小，则插入父节点的左子树
if (cmp < 0)
parent.left = e;
//如果key比父节点的key大，则插入父节点的右子树
else
parent.right = e;
//重新调整红黑树
fixAfterInsertion(e);
size++;
modCount++;
return null;
} //插入节点后，调整红黑树结构
private void fixAfterInsertion(Entry<K,V> x) {
//新插入的叶子节点一定是红色的
x.color = RED;
//插入节点不是null且不为root且父节点是红色才需要调整
while (x != null && x != root && x.parent.color == RED) {
//如果当前节点的父节点是其父节点的左子树
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
//取父节点的兄弟节点y
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
//如果y是红色的，将父节点及其兄弟节点都设为黑色，将父节点的父节点设为红色并赋值给x，继续向上调整
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
//如果y是黑色的，说明y有子节点
} else {
//如果x是右子树
if (x == rightOf(parentOf(x))) {
//将x的父节点设为x
x = parentOf(x);
//以x为中心进行左旋，通过左旋保证x为左子树
rotateLeft(x);
}
//将x的父节点设为黑色
setColor(parentOf(x), BLACK);
//将x父节点的父节点设为红色
setColor(parentOf(parentOf(x)), RED);
//再将以x的父节点的父节点为中心进行右旋
rotateRight(parentOf(parentOf(x)));
}
//如果当前节点的父节点是其父节点的右子树
} else {
//取当前节点的兄弟节点y
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
//如果y是红色的，则将x的父节点和y都设为黑色，将父节点的父节点设为红色并赋值给x，继续向上调整
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
//如果y是黑色的，说明y有子节点
} else {
//如果x是左子树
if (x == leftOf(parentOf(x))) {
//将x的父节点设为x
x = parentOf(x);
//以x为中心进行右旋，通过右旋保证x为右子树
rotateRight(x);
}
//将x父节点的父节点设为黑色
setColor(parentOf(x), BLACK);
//将x父节点的父节点设为红色
setColor(parentOf(parentOf(x)), RED);
//以x的父节点的父节点为中心进行左旋
rotateLeft(parentOf(parentOf(x)));
}
}
}
//保证根节点是黑色的
root.color = BLACK;
}
5. 删除节点
删除要先复用查找逻辑来查找到要删除的节点，找到后删除并自平衡，而要删除的节点会存在下面三种情况：
1. 删除节点无子节点：直接删除，如果是root节点或者是红色的则直接删除，如果是非root节点则删除后以删除节点为轴心进行自平衡。
2. 删除节点只有一个子节点：用删除节点的唯一子节点代替删除节点，如果删除节点是红色则直接删除，如果是黑色则删除后以替换节点为轴心进行自平衡。
3. 删除节点有两个子节点：通过删除节点的后继节点(删除节点右子树中最左的节点)来代替删除节点，然后删除后继节点来简化删除操作，如果后继节点有右子节点则变为第2种情况，如果后继节点没有子节点则变为第1中情况。
其中情况3是很复杂的场景，但是采用后继节点的思路大大简化了这部分逻辑，删除节点的操作很简单，关键在于如何保持平衡。只有当删除节点时黑色时候才会进行自平衡，所以此时替换节点所在分支少了一个黑色节点，故需要将其兄弟节点的分支减少一个黑色节点或者向兄弟节点借一个黑色节点来保持平衡，具体自平衡的情况可分为以下情况：
1. 替换节点是左子节点，兄弟节点是黑色，兄弟节点的两个子节点都是黑色：直接将兄弟节点设为红色，如果父节点是红色，将父节点改为黑色便可保证红黑树的平衡，下图删除节点也可能是后继节点（把后继节点的属性赋给删除节点，简化为删除后继节点操作），如果父节点是黑色，相当于父节点下面的分支少了一个黑色节点，继续以父节点为基点向上进行自平衡操作。
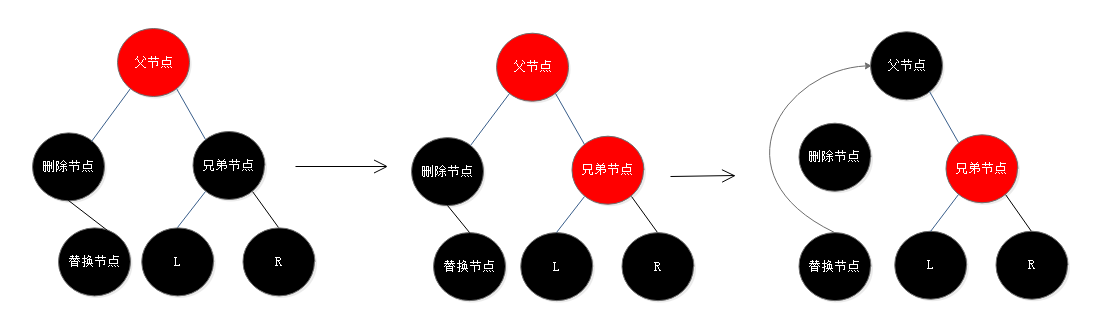
2. 替换节点是左子节点，兄弟节点是黑色，兄弟节点的左子节点是任意颜色，兄弟节点的右子节点为红色：将兄弟节点设为父节点的颜色，父节点设为黑色，兄弟节点的右子节点设为黑色，然后以父节点为轴心进行一次左旋操作将兄弟节点变为祖父节点（原父节点颜色），这时替换节点所在分支多了一个黑色节点（父节点），此时红黑树已达到平衡条件；
3. 替换节点是左子节点，兄弟节点是黑色，兄弟节点的左子节点是红色，兄弟节点的右子节点为黑色：将兄弟节点的左子节点设为黑色，兄弟节点设为红色，以兄弟节点为轴心进行一次右旋操作将转换为情况2；
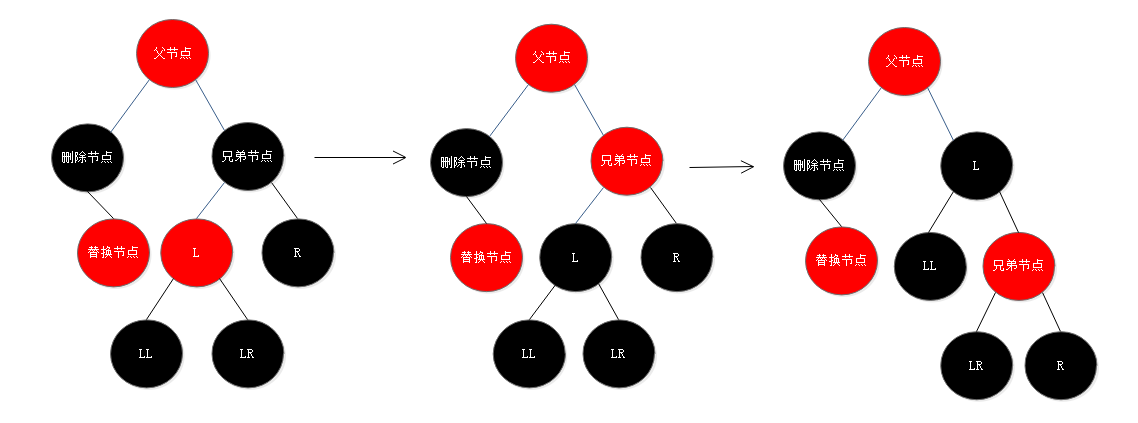
4. 替换节点是左子节点，兄弟节点是红色：将兄弟节点设为黑色，父节点设为红色，以父节点为轴心进行一次左旋操作使父节点变为原兄弟节点的左子节点，而原兄弟节点的左子节点变为父节点的右子节点（也就是替换节点的兄弟节点，一定是黑色的，因为原兄弟节点是红色的），这时就转为情况1、2、3中的一种；
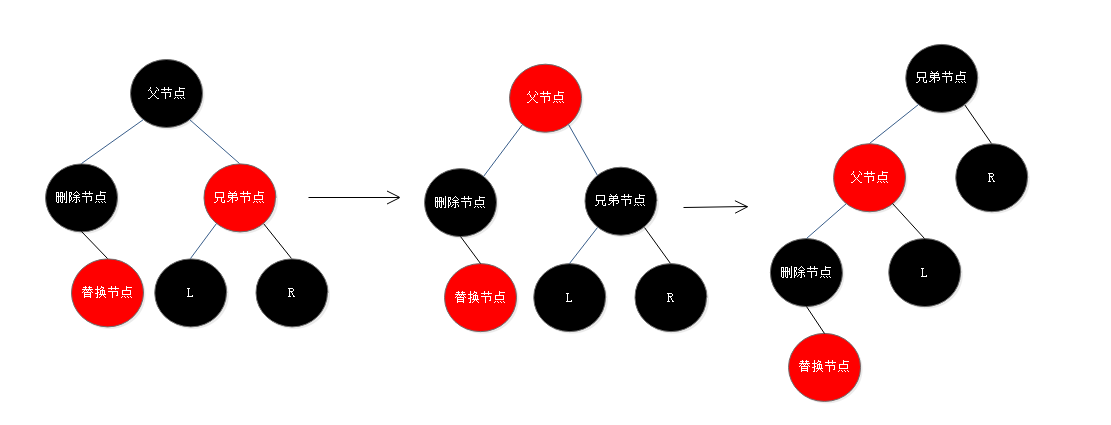
5. 替换节点时右子节点，兄弟节点是黑色，兄弟节点的两个子节点都是黑色：直接将兄弟节点设为红色
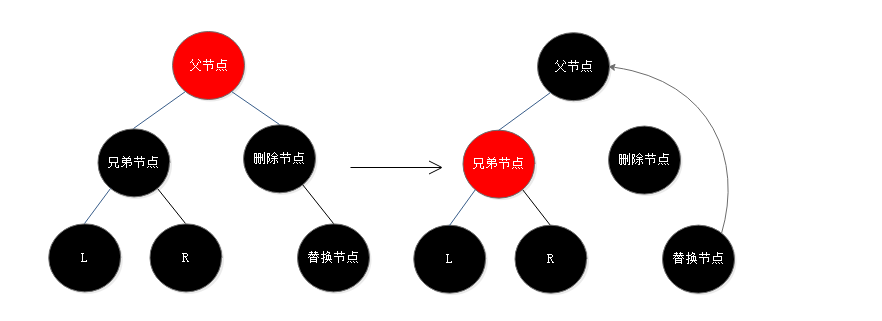
6. 替换节点时右子节点，兄弟节点是黑色，兄弟节点的右子节点是任意颜色，兄弟节点的左子节点为红色：将兄弟节点设为父节点的颜色，父节点设为黑色，兄弟节点的左子节点设为黑色，然后以父节点为轴心进行一次右旋操作将兄弟节点变为祖父节点（原父节点颜色），这时替换节点所在分支多了一个黑色节点（父节点），此时红黑树已达到平衡条件；
7. 替换节点时右子节点，兄弟节点是黑色，兄弟节点的右子节点是红色，兄弟节点的左子节点为黑色：将兄弟节点的右子节点设为黑色，兄弟节点设为红色，以兄弟节点为轴心进行一次左旋操作将转换为情况6；
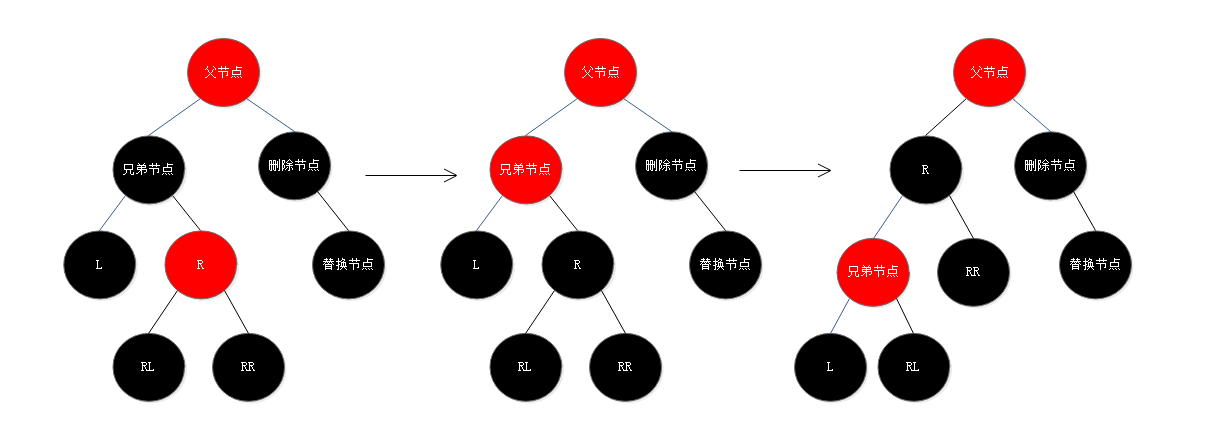
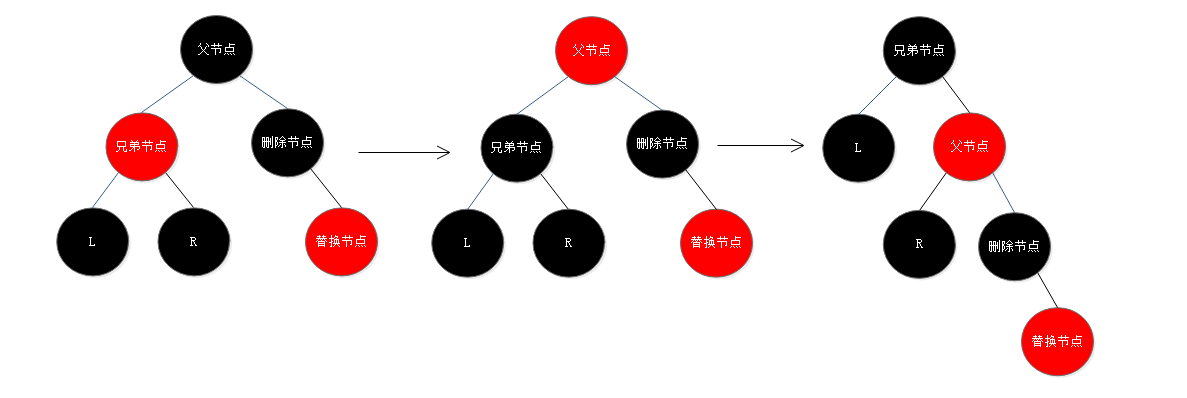
8. 替换节点时右子节点，兄弟节点是红色：将兄弟节点设为黑色，父节点设为红色，以父节点为轴心进行一次右旋操作使父节点变为原兄弟节点的右子节点，而原兄弟节点的右子节点变为父节点的左子节点（也就是替换节点的兄弟节点，一定是黑色的，因为原兄弟节点是红色的），这时就转为情况5、6、7中的一种；
//删除节点p
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--; //如果p有2个子节点，寻找p的后继节点（大于p的最小节点）来替换p节点，使p节点最多只有一个子节点
if (p.left != null && p.right != null) {
//successor根据p的右子树依次寻找其下面的左子树，直到找到左节点为空的节点返回
//如果p的右子树为空，则向上取父节点，直到找到第一个为左节点的节点，但这里p的右子树肯定不会空
Entry<K,V> s = successor(p);
//将继承节点的key-value赋给删除节点
p.key = s.key;
p.value = s.value;
//将删除节点的操作变为删除继承节点
p = s;
} //上面已经保证p最多只有一个子节点了，如果有一个子节点，则由子节点直接代替p节点即可，
//如果没有子节点，则直接删除p节点即可
Entry<K,V> replacement = (p.left != null ? p.left : p.right); //如果replacement不为空，p节点由replacement代替，删除p后自平衡
if (replacement != null) {
//将p的父节点设为replacement的父节点
replacement.parent = p.parent;
//如果p的父节点为空，将replacement设为root
if (p.parent == null)
root = replacement;
//如果p是左子树，则将replacement设为p的父节点的左子树
else if (p == p.parent.left)
p.parent.left = replacement;
//如果p是右子树，则将replacement设为p的父节点的右子树
else
p.parent.right = replacement; //删除p节点
p.left = p.right = p.parent = null; //如果删除的是黑色节点，就会破坏红黑树的规则：从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
//所以这时候就需要重新调整红黑树的结构，而删除的是红色节点就没有影响
if (p.color == BLACK)
fixAfterDeletion(replacement);
//p是叶子节点且没有父节点，则p是root节点，直接删除root
} else if (p.parent == null) { // return if we are the only node.
root = null;
//p是叶子节点且不是root
} else {
//如果删除的是黑色节点，就会破坏红黑树的规则：从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
if (p.color == BLACK)
fixAfterDeletion(p); //删除节点p
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
} //删除节点后调整红黑树结构
private void fixAfterDeletion(Entry<K,V> x) {
//当前节点x是黑色的非root节点
while (x != root && colorOf(x) == BLACK) {
//【替换节点是左子节点】
if (x == leftOf(parentOf(x))) {
//取x的兄弟节点sib
Entry<K,V> sib = rightOf(parentOf(x)); //【兄弟节点是红色】
//通过下面操作将转为【兄弟节点是黑色】的情况
if (colorOf(sib) == RED) {
//将sib设为黑色
setColor(sib, BLACK)
//将父节点设为红色
setColor(parentOf(x), RED);
//以父节点为轴心进行一次右旋操作使父节点变为原兄弟节点的右子节点，而原兄弟节点的右子节点变为父节点的左子节点（也就是替换节点的兄弟节点，一定是黑色的，因为原兄弟节点是红色的）
rotateLeft(parentOf(x));
//重新取调整后的兄弟节点
sib = rightOf(parentOf(x));
} //【兄弟节点是黑色】 //【兄弟节点的两个子节点都是黑色】
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
//直接将兄弟节点设为红色，继续以父节点为轴心进行自平衡
setColor(sib, RED);
x = parentOf(x);
} else {
//【兄弟节点的左子节点为红色，兄弟节点的右子节点为黑色】
//将兄弟节点的左子节点设为黑色，兄弟节点设为红色，以兄弟节点为轴心进行一次右旋操作将转换为【兄弟节点的右子节点为红色】的情况
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
//【兄弟节点的右子节点为红色】
//将兄弟节点设为父节点的颜色，父节点设为黑色，兄弟节点的右子节点设为黑色
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
//以父节点为轴心进行一次左旋操作将兄弟节点变为祖父节点（原父节点颜色），
rotateLeft(parentOf(x));
//这时替换节点所在分支多了一个黑色节点（父节点），此时红黑树已达到平衡条件，x设为root跳出循环；
x = root;
}
//【替换节点是右子节点】
} else {
//取x的兄弟节点sib
Entry<K,V> sib = leftOf(parentOf(x)); //【兄弟节点是红色】
if (colorOf(sib) == RED) {
//将兄弟节点设为黑色，父节点设为红色
setColor(sib, BLACK);
setColor(parentOf(x), RED);
//以父节点为轴心进行一次右旋操作使父节点变为原兄弟节点的右子节点，而原兄弟节点的右子节点变为父节点的左子节点（也就是替换节点的兄弟节点，一定是黑色的，因为原兄弟节点是红色的）
rotateRight(parentOf(x));
//这时就转为【兄弟节点是黑色】的情况
sib = leftOf(parentOf(x));
} //【兄弟节点是黑色】 //【兄弟节点的两个子节点都是黑色】
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
//直接将兄弟节点设为红色，继续以父节点为轴心进行自平衡
setColor(sib, RED);
x = parentOf(x);
} else {
//【兄弟节点的右子节点是红色，兄弟节点的左子节点为黑色】
if (colorOf(leftOf(sib)) == BLACK) {
//将兄弟节点的右子节点设为黑色，兄弟节点设为红色
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
//以兄弟节点为轴心进行一次左旋操作将转换为【兄弟节点的左子节点为红色】的情况；
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
//【兄弟节点的左子节点为红色】
//将兄弟节点设为父节点的颜色，父节点设为黑色，兄弟节点的左子节点设为黑色
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
//然后以父节点为轴心进行一次右旋操作将兄弟节点变为祖父节点（原父节点颜色），这时替换节点所在分支多了一个黑色节点（父节点）
rotateRight(parentOf(x));
//此时红黑树已达到平衡条件，x设为root跳出循环；
x = root;
}
}
}
//上面有两种情况跳出循环，x==root或者x是红色。巧妙的是如果x的兄弟节点的子节点只要有一个是红色，最多进行3次左/右旋操作（兄弟节点是红色时最多3次，黑色时最多2次）便可以达到平衡，并把x设为root，这时把root设为黑色保证根节点是黑色
//如果x的兄弟节点的子节点两个子节点都是黑色，不要进行树的旋转，只将兄弟节点设为红色并将x设为父节点，如果父节点是红色，则直接跳出循环，这时把父节点设为黑色刚好保持了树的平衡
setColor(x, BLACK);
}
学习JDK1.8集合源码之--TreeMap的更多相关文章
- 【JDK1.8】JDK1.8集合源码阅读——TreeMap（一）
一.前言 在前面两篇随笔中,我们提到过,当HashMap的桶过大的时候,会自动将链表转化成红黑树结构,当时一笔带过,因为我们将留在本章中,针对TreeMap进行详细的了解. 二.TreeMap的继承关 ...
- 【JDK1.8】JDK1.8集合源码阅读——TreeMap（二）
一.前言 在前一篇博客中,我们对TreeMap的继承关系进行了分析,在这一篇里,我们将分析TreeMap的数据结构,深入理解它的排序能力是如何实现的.这一节要有一定的数据结构基础,在阅读下面的之前,推 ...
- 学习JDK1.8集合源码之--LinkedHashSet
1. LinkedHashSet简介 LinkedHashSet继承自HashSet,故拥有HashSet的全部API,LinkedHashSet内部实现简单,核心参数和方法都继承自HashSet,只 ...
- 学习JDK1.8集合源码之--ArrayList
参考文档: https://cloud.tencent.com/developer/article/1145014 https://segmentfault.com/a/119000001857894 ...
- 学习JDK1.8集合源码之--WeakHashMap
1. WeakHashMap简介 WeakHashMap继承自AbstractMap,实现了Map接口. 和HashMap一样,WeakHashMap也是一种以key-value键值对的形式进行数据的 ...
- 学习JDK1.8集合源码之--HashMap
1. HashMap简介 HashMap是一种key-value结构存储数据的集合,是map集合的经典哈希实现. HashMap允许存储null键和null值,但null键最多只能有一个(HashSe ...
- 学习JDK1.8集合源码之--ArrayDeque
1. ArrayDeque简介 ArrayDeque是基于数组实现的一种双端队列,既可以当成普通的队列用(先进先出),也可以当成栈来用(后进先出),故ArrayDeque完全可以代替Stack,Arr ...
- 学习JDK1.8集合源码之--TreeSet
1. TreeSet简介 TreeSet是Set的实现类之一,是不可重复集合,非线程安全的. TreeSet是SortedSet的唯一实现类,实现了元素的自动排序,排序不是以插入的顺序排序,而是默认以 ...
- 学习JDK1.8集合源码之--HashSet
1. HashSet简介 HashSet是一个不可重复的无序集合,底层由HashMap实现存储,故HashSet是非线程安全的,由于HashSet使用HashMap的Key来存储元素,而HashMap ...
随机推荐
- 集合划分——cf1028D思维题
非常思维的一道题目,题意很长 给定s1,s2两个集合,s1维护最大值,s2维护最小值,s1的所有元素要比s2小 操作1:往两个集合里的任意一个添加x 操作2:把x从所在的集合里删掉:要求被删的x必须是 ...
- axios请求头几种区别:application/x-www-form-urlencoded
今天小伙伴问我们项目axios默认请求头是application/x-www-form-urlencoded;charset=UTF-8, 现在有个后端接口要求请求头方式为application/js ...
- CSS自动换行、强制不换行、强制断行、超出显示省略号
转自:https://blog.csdn.net/liuyan19891230/article/details/50969393 P标签是默认是自动换行的,因此设置好宽度之后,能够较好的实现效果,但是 ...
- lumen框架使用Elasticsearch详解
该博文是集合几个博客踩坑得来的,百度热搜前几篇都是缺胳膊少腿的,所以结合几篇博客实现了一遍. 一.lumen使用Elasticsearch 首先需要搭建好的elasticsearch环境: http: ...
- C# StructLayout(LayoutKind.Sequential)]
结构体是由若干成员组成的.布局有两种1.Sequential,顺序布局,比如struct S1{ int a; int b;}那么默认情况下在内存里是先排a,再排b也就是如果能取到a的地址,和b的 ...
- Linux虚拟机ip为127.0.0.1的处理
Redhat系列(Cnetos)打配置文件在/etc/sysconfig/network-scripsts/ifcfg-eth0(在Centos6.5开始就有这种情况了) 打开配置文件找到ONBOOT ...
- 报错initscripts conflicts with redhat-release-server-7.0-1.el7.x86_64
报错 解决:删除冲突的rpm包即可 rpm -e redhat-release-server-7.0-1.el7.x86_64 --nodeps
- 【bzoj 4671】 异或图
题目 神仙题啊神仙题 显然这个东西一脸不可求的样子啊,这种东西我们显然需要搞一个容斥什么的 于是设\(g_i\)表示至少存在\(i\)个联通块(联通块内部的边没有要求,联通块和联通块之间不存在边)的方 ...
- 第12章 SQL联接
第12章 SQL联接 关系数据库的3个支柱:选择.投影和联接. 两种基本的连接同等联接和非同等联接. 源表和目标表有相同的名称的列,就可以在他们之间执行自然联接,而无需指定连接列. 自然join us ...
- 07-img和a标签
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...