leetcode-229-求众数②

题目描述：

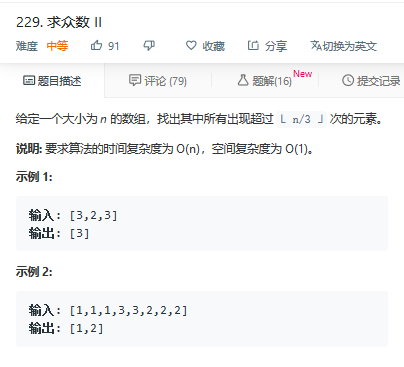
方法一：摩尔投票法

class Solution:
    def majorityElement(self, nums: List[int]) -> List[int]:
        candiate1 = candiate2 = None
        cnt1 = cnt2 = 0
        for num in nums:
            if num == candiate1:
                cnt1 += 1
            elif num == candiate2:
                cnt2 += 1
            elif cnt1 == 0:
                candiate1 = num
                cnt1 = 1
            elif cnt2 == 0:
                candiate2 = num
                cnt2 = 1
            else:
                cnt1 -= 1
                cnt2 -= 1
        return [n for n in (candiate1, candiate2) if nums.count(n)>len(nums)//3]

附：169 求众数1

题目描述：

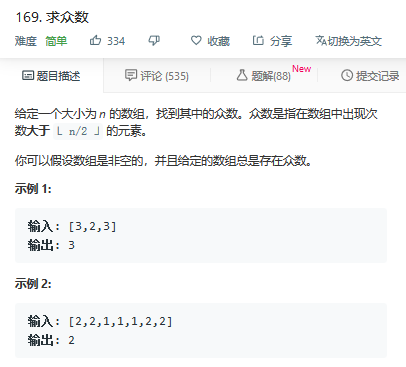
class Solution:
    def majorityElement(self, nums):
        count = 0
        candidate = None

        for num in nums:
            if count == 0:
                candidate = num
            count += (1 if num == candidate else -1)

        return candidate