小小知识点（二十）利用MATLAB计算定积分

一重定积分

1. Z = trapz(X,Y,dim) 
梯形数值积分，通过已知参数x,y按dim维使用梯形公式进行积分

%举例说明1

clc
clear all
% int(sin(x),0,pi)
x=0:pi/100:pi; %积分区间
y=sin(x); %被积函数
z = trapz(x,y) %计算方式一
z = pi/100*trapz(y) %计算方式二 

运行结果

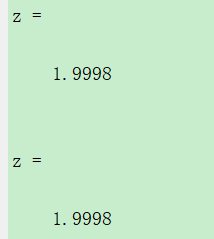
被积函数曲线

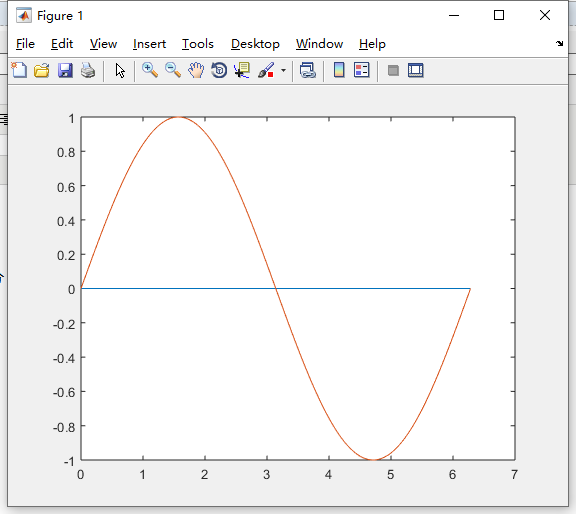
2、[q,fcnt]= quad(fun,a,b,tol,trace,p1,p2...) 
自适应simpson公式数值积分，适用于精度要求低，积分限[a,b]必须是有限的,被积函数平滑性较差的数值积分.

[q,fcnt] = quadl(fun,a,b,tol,trace,p1,p2...)

自适应龙贝格数值积分，适用于精度要求高，积分限[a,b]必须是有限的，被积函数曲线比较平滑的数值积分

%举例说明2
% 被积函数1/(x^3-2*x-p)，其中参数p=5，积分区间为[0,2]
clc
clear all
F = @(x,n)1./(x.^3-2*x-n); %被积函数
Q1 = quad(@(x)F(x,5),0,2)   %计算方式一
Q1 = quad(F,0,2,[],[],5)    %计算方式二

Q2 = quadl(@(x)F(x,5),0,2)   %计算方式一
Q2 = quadl(F,0,2,[],[],5)    %计算方式二

运行结果

被积函数曲线

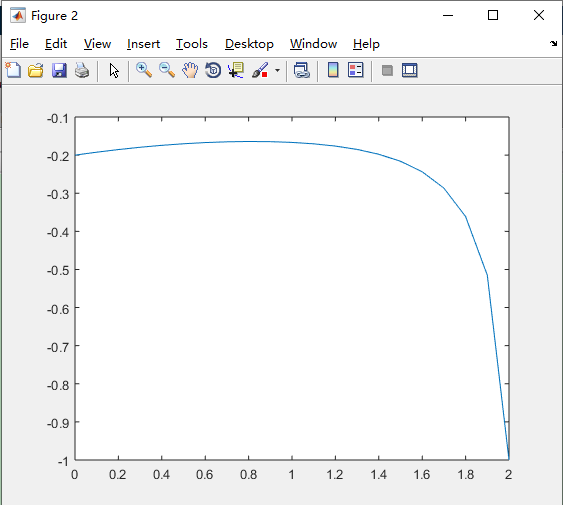
可能警告： 
1.'Minimum step size reached' 
意味着子区间的长度与计算机舍入误差相当，无法继续计算了。原因可能是有不可积的奇点

2.'Maximum function count exceeded'  
意味着积分递归计算超过了10000次。原因可能是有不可积的奇点

3.'Infinite or Not-a-Number function value encountered'

意味着在积分计算时，区间内出现了浮点数溢出或者被零除。

3、[q,errbnd] = quadgk(fun,a,b,param1,val1,param2,val2,...)

自适应Gauss-Kronrod数值积分，适用于高精度和震荡数值积分，支持无穷区间，并且能够处理端点包含奇点的情况，同时还支持沿着不连续函数积分，复数域线性路径的围道积分法

注意事项： 
1.积分限[a,b]可以是[-inf,inf]，但必须快速衰减 
2.被积函数在端点可以有奇点，如果区间内部有奇点，将以奇点区间划分成多个，也就是说奇点只能出现在端点上 
3.被积函数可以剧烈震荡 
4.可以计算不连续积分，此时需要用到'Waypoints'参数，'Waypoints'中的点必须严格单调

5.可以计算围道积分，此时需要用到'Waypoints'参数，并且为复数，各点之间使用直线连接

6.param,val为函数的其它控制参数，比如上面的'waypoints'就是，具体看帮助

出现错误： 
1.'Reached the limit on the maximum number of intervals in use'

2.'Infinite or Not-a-Number function value encountered'

%举例说明3
%（1）计算有奇点积分
clc
clear all
F=@(x)exp(x).*log(x);
Q = quadgk(F,0,1) 　　

运行结果

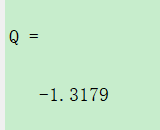
被积函数曲线

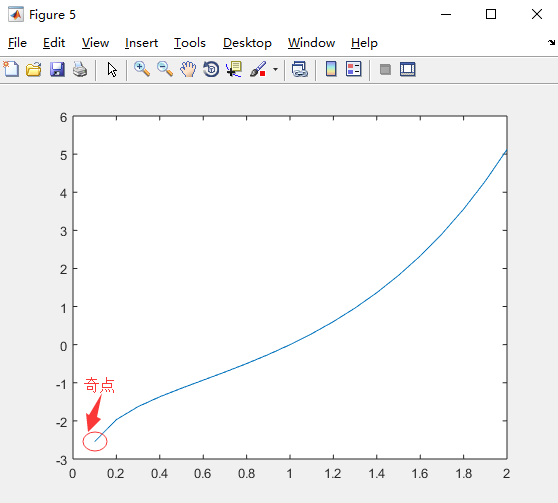
%举例说明3
%（2）计算半无限震荡积分
clc
clear all
F=@(x)x.^5.*exp(-x).*sin(x);
fplot(F,[0,100])%绘图，看看函数的图形
[q,errbnd] = quadgk(F,0,inf,'RelTol',1e-8,'AbsTol',1e-12)%积分限中可以有inf，但必须快速收敛 　

运行结果

被积函数曲线

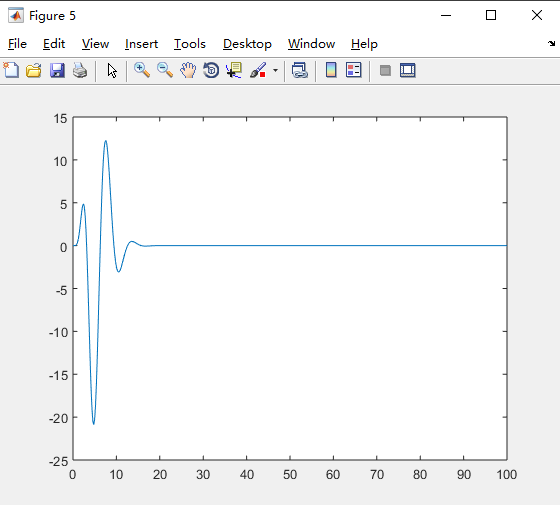
%举例说明3
%（3）计算不连续积分
clc
clear all
F=@(x)x.^5.*exp(-x).*sin(x);
[q,errbnd] = quadgk(F,1,10,'Waypoints',[2 5])%显然2，5为间断点 

运行结果

被积函数曲线

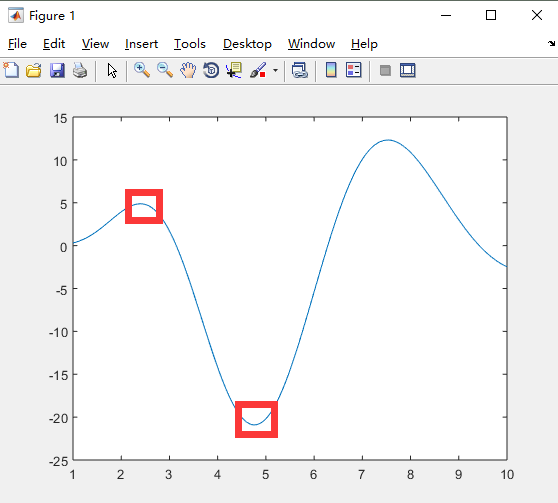
4、[Q,fcnt] = quadv(fun,a,b,tol,trace) 矢量化自适应simpson数值积分

注意事项： 
1.该函将quad函数矢量化了，就是一次可以计算多个积分

2.所有的要求完全与quad相同

%举例说明4
% 计算下面积分，分别计算n=1,2...,5时的5个积分值，被积函数1/(n+x)，积分限为[0,1]
clc
clear all
%计算多个积分值（一）
for k = 1:5,
    Qs(k) = quadv(@(x)1/(k+x),0,1)
end;
%同时%计算多个积分值的方法（二）
F=@(x,n)1./((1:n)+x);%定义被积函数
quadv(@(x)F(x,5),0,1)%我们可以完全使用quadv函数替换上面循环语句的，建议使用（二）

运行结果：

二重积分

q = dblquad(fun,xmin,xmax,ymin,ymax,tol,method) 
矩形区域二重数值积分，一般区域二重积分参见NIT(数值积分工具箱)的quad2dggen函数

% 例 计算下面二重积分  

F = @(x,y)y*sin(x)+x*cos(y);

Q = dblquad(F,pi,2*pi,0,pi) 

三重定积分

q=triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol,method)

长方体区域三重数值积分，注意此时没有一般区域的三重积分

%例 计算下面三重积分

F = @(x,y,z)y*sin(x)+z*cos(x);

Q = triplequad(F,0,pi,0,1,-1,1) 

超维长方体区域多重积分

quadndg：NIT工具箱函数，可以解决多重超维长方体边界的定积分问题，但没有现成的一般积分区域求解函数

总结

quad：采用自适应变步长simpson方法，速度和精度都是最差的，建议不要使用

quad8：使用8阶Newton-Cotes算法，精度和速度均优于quad，但在目前版本下已被取消

quadl：采用lobbato算法，精度和速度均较好，建议全部使用该函数

quadg：NIT(数值积分)工具箱函数，效率最高，但该工具箱需要另外下载

quadv：quad的矢量化函数，可以同时计算多个积分

quadgk：很有用的函数，功能在Matlab中最强大 
quad2dggen：一般区域二重积分，效率很好，需要NIT支持

dblquad：长方形区域二重积分 (

triplequadL：长方体区域三重积分 
quadndg：超维长方体区域积分，需要NIT支持