CCPC-Wannafly Winter Camp Day1 (Div2 ABCFJ) 待补...

Day1 Div2 场外链接

按题目顺序~

A 机器人 传送门

题意：有两条平行直线A、B，每条直线上有n个点，编号为1~n。在同一直线上，从a站点到b站点耗时为两点间的距离。存在m个特殊站点，只有在特殊站点才能到另一条直线上的对应编号站点，耗时K，且只有在特殊站点才能掉头，否则只能沿同一方向走。另外1号和n号站点为特殊站点。问从A直线上的s站点开始，经过r个给定的站点并回到原处最少需要的时间。

题解：我们可以分成两种大的情况讨论：

　　1.给定的点都在A直线上，耗时等于路程。此时站点的分布有三种情况：s左右两边均存在、都在s左边、都在s右边。

　　1）当给定的点在s左右两边都存在时，最少需要的时间为：s到 给定的最左边站点左边第一个特殊站点al（若它本身是特殊站点  站点al  就是该站点本身）距离的两倍（来回）+ s到 给定的最右边站点右边第一个特殊站点ar（若它本身是特殊站点  站点ar  就是该站点本身）距离的两倍（来回），即al到ar距离的两倍；

　　2）当点都在s左边时，最少需要的时间为从s到 给定的最左边站点左边第一个特殊站点al（若它本身是特殊站点  站点al  就是该站点本身）距离的两倍（来回），此时把s也看成特殊点可以将s看做ar，那么最少需要的时间为al到ar距离的两倍；

　　3）当点都在s左边时，同理，最少需要的时间为从s到 给定的最右边站点右边第一个特殊站点ar（若它本身是特殊站点  站点ar  就是该站点本身）距离的两倍（来回），此时可以将s看做al，那么最少需要的时间为al到ar距离的两倍；

　　总的来说，当给定点都在A直线上时，最少需要的时间为为al到ar距离的两倍。al为给定的最左边的站点（若它是特殊站点）否则为其左边第一个特殊站点；ar同理。

　　2.存在给定点在B直线上时，最少需要通过特殊点跨直线两次。我们可以看下图：

　　

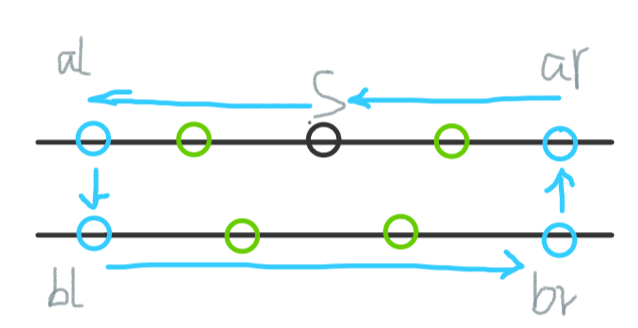
由图可知最小时间为：ar-al + br-bl + al-bl + br-ar + 2*k

为了防止都在一边的情况，在算al和ar时将s当做特殊站点计算，bl初始化为0，br初始化为n+1后面直接更新即可，不会影响bl和br的距离。

代码如下：

#include<bits/stdc++.h>
#define PI 3.141592653589793238462643383279
using namespace std;
typedef long long ll;
const int N = 1e5+;
const ll mod = ;
struct node{
    int x, y;
}a[N];
int p[];
int main(){
    int n,r,m,k,s;
    scanf("%d%d%d%d%d",&n,&r,&m,&k,&s);
    int flag=,al=s,ar=s,bl=n+,br=;
    for (int i=;i<r;i++){
        scanf("%d%d",&a[i].x,&a[i].y);
        if (a[i].y) flag=,bl=min(bl,a[i].x),br=max(br,a[i].x);
        al=min(al,a[i].x);
        ar=max(ar,a[i].x);
    }
    for (int i=;i<m;i++) scanf("%d",&p[i]);
    p[m]=,p[m+]=n;
    sort(p,p+m+);
    if (flag){
        for (int i=;;i++)
        if (p[i]>bl) {
            bl=p[i-];
            break;
        }
        for (int i=m+;;i--)
        if (p[i]<br){
            br=p[i+];
            break;
        }
    }
    p[m+]=s;
    sort(p,p+m+);
    for (int i=;;i++)
    if (p[i]>al){
        al=p[i-];
        break;
    }
    for (int i=m+;;i--)
    if (p[i]<ar){
        ar=p[i+];
        break;
    }
    ll ans=;
    if (!flag) ans=1ll*(ar-al)*;
    else {
        al=min(al,bl);
        ar=max(ar,br);
        ans=ar-al+br-bl+k*+bl-al+ar-br;
    }
    printf("%lld\n",ans);
    return ;
}

B 吃豆豆  传送门

题意：有一个n行m列的棋盘，对于第i行第j列的格子，每过T[i][j]秒会出现一个糖果，糖果仅会在出现的那一秒存在，下一秒就会消失。假如你在第i行第j列格子上，你可以选择上下左右走一格，或者停在原地。现在指定初始位置和终点，问你从初始位置出发，初始时间为0秒，到终点的路上至少得到 C个糖果最少需要的时间。

题解：因为 n,m≤10，所以可以用搜索来做。从初始位置开始，直到到达终点且糖果数≥C时输出结果，程序终止。

代码如下：

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = +;
bool vis[][][];
int t[][],dp[][][];
int d[][]={,,,,,-,-,,,};
int main() {
    int n,m,c,xs,xt,ys,yt;
    scanf("%d%d%d",&n,&m,&c);
    for (int i=;i<=n;i++)
        for (int j=;j<=m;j++)
            scanf("%d",&t[i][j]);
    scanf("%d%d%d%d",&xs,&ys,&xt,&yt);
    memset(vis,false,sizeof(vis));
    vis[xs][ys][]=;
    for (int k=;;k++){
        for (int i=;i<=n;i++)
            for (int j=;j<=m;j++)
                if (vis[i][j][k-]) {
                    for (int l=;l<;l++){
                        int x=i+d[l][];
                        int y=j+d[l][];
                        if (x<||x>n||y<||y>m) continue;
                        vis[x][y][k]=;
                        if (k%t[x][y]==) dp[x][y][k]=max(dp[i][j][k-]+,dp[x][y][k]);
                        else dp[x][y][k]=max(dp[x][y][k],dp[i][j][k-]);
                        if (x==xt&&y==yt&&dp[x][y][k]>=c){
                            printf("%d\n",k);
                            return ;
                        }
                    }
                }
    }
    return ;
}

C 拆拆拆数 传送门

题意：给你两个数A、B，把A拆成a1,a2...an，把B拆成b1,b2...bn，需满足：

　　1.对所有i (1 ≤ i ≤ n)，ai,bi ≥2 且 gcd(ai,bi) = 1;

　　2.a1+a2+...+an=A , b1+b2+...+bn=B

　　输出n最小的任意一组。

题解：当gcd(A,B)=1时，直接输出A,B；否则，拆成两个数就行了（待证），那么我们可以直接 i 从2开始暴力枚举，如果gcd(A-i,i)=1且gcd(i,B-i)=1输出即可。

代码如下：

#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main() {
    int t;
    ll a,b;
    scanf("%d",&t);
    while(t--){
        scanf("%lld%lld",&a,&b);
        if (__gcd(a,b)==) {
            printf("1\n%lld %lld\n",a,b);
            continue;
        }
        for (ll i=;;i++){
            if (__gcd(a-i,i)==&&__gcd(i,b-i)==){
                printf("2\n%lld %lld\n%lld %lld\n",a-i,i,i,b-i);
                break;
            }
        }
    }
    return ;
}

F 爬爬爬山 传送门

题意：有n座山，m条路。初始有k点体力，爬山过程中，所处海拔每上升1m，体力值-1，每下降1m，体力值+1。体力值不能为负，所以需要事先将山的高度降低，降低 l 米需要耗费l*l的价值，且每座山只能降一次。从1号山顶出发，所以1号山高度不能变。问：从1号山到n号山的总代价最小为多少：降低山消耗的价值+走过的路的总长度。

题解：显然每条路只会走一次，也就是说每座山只会走这一条路到达且只会到达一次，所以我们在给两座山加路的时候可以把需要降低山的价值加到路的权值里面。稀疏图+最短路即可。这里我用的链式向前星建图。

代码如下：

#include<bits/stdc++.h>
#define ll long long
#define pr pair<ll,int>
#define mp make_pair
using namespace std;
const int N = 1e5+;
const ll INF = 0x3f3f3f3f;
struct node
{
    int to,next;
    ll w;
}e[N<<];
ll h[N],dis[N];
int head[N],cnt;
bool vis[N];

void init()
{
    cnt=;
    memset(head,-,sizeof(head));
}

void add(int u,int v,ll w)
{
    e[cnt].to=v;
    e[cnt].w=w;
    e[cnt].next=head[u];
    head[u]=cnt++;
}

void dij(int n)
{
    memset(vis,false,sizeof(vis));
    memset(dis,INF,sizeof(dis));
    priority_queue <pr> q;
    dis[] = ;
    q.push(mp(,));
    while(!q.empty())
    {
        int x = q.top().second;
        q.pop();
        for (int i = head[x]; ~i; i=e[i].next)
        {
            if (dis[e[i].to]>dis[x]+e[i].w)
            {
                dis[e[i].to]=dis[x]+e[i].w;
                q.push(mp(-dis[e[i].to],e[i].to));
            }
        }
    }
    printf("%lld\n",dis[n]);
}

int main()
{
    int n,m,u,v;
    ll k,w;
    init();
    scanf("%d%d%lld",&n,&m,&k);
    for (int i=;i<=n;i++)
        scanf("%lld",&h[i]);
    k+=h[];
    for (int i=;i<m;i++)
    {
        scanf("%d%d%lld",&u,&v,&w);
        if (h[u]-k>) add(v,u,w+(h[u]-k)*(h[u]-k));
        else add(v,u,w);
        if (h[v]-k>) add(u,v,w+(h[v]-k)*(h[v]-k));
        else add(u,v,w);
    }
    dij(n);
    return ;
}

J 夺宝奇兵 传送门

题意：有n个居民，他们一共有m件宝物，对于第i件宝物，wls可以花费a1的金币买过来，问wls最少要准备多少金币，才能使他成为宝物最多的（＞其他任何人的）。

题解：因为n,m≤1000，数据量比较小，所以我们可以枚举要买的宝物件数，先把比这个数量多的居民的宝物按价格从低到高买，若≤要买的数量，则再每买过的宝物里按价格从低到高买，更新答案。

代码如下：

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = +;
struct node
{
    ll a;
    int c,pos;
}b[N],c[N];
bool vis[N];
bool cmp1(node i,node j)
{
    return i.a<j.a;
}
bool cmp2(node i,node j)
{
    if (i.c == j.c)
        return i.a>j.a;
    return i.c<j.c;
}
int main()
{
    ll x;
    int n,m,y;
    scanf("%d%d",&n,&m);
    for (int i=;i<=m;i++)
    {
        scanf("%lld%d",&x,&y);
        b[i].a=x;
        b[i].c=y;
        b[i].pos=i;
        c[i]=b[i];
    }
    sort(b+,b++m,cmp1);
    sort(c+,c++m,cmp2);
    ll mmax=1e17;
    for (int need=;need<=m;need++)
    {
        ll ans=;
        int have=,k=;
        memset(vis,false,sizeof(vis));
        for (int j=;j<=m;j++)
        {
            if (c[j-].c != c[j].c) k=;
            else k++;
            if (k>need)
            {
                have++;
                ans+=c[j].a;
                vis[c[j].pos]=true;
            }
        }
        if (have<=need)
        {
            for (int j=;j<=m;j++)
            {
                if (!vis[b[j].pos])
                {
                    have++;
                    vis[b[j].pos]=true;
                    ans+=b[j].a;
                    if (have>need) break;
                }
            }
        }
        if (have>need)
            mmax=min(mmax,ans);
    }
    printf("%lld\n",mmax);
    return ;
}

其他题待补。。。