第三十四篇 玩转数据结构——哈希表（HashTable）

1.. 整型哈希函数的设计

• 小范围正整数直接使用
• 小范围负整数整体进行偏移
• 大整数，通常做法是"模一个素数"

 

2.. 浮点型哈希函数的设计

• 转成整型进行处理

 

3.. 字符串哈希函数的设计

• 转成整型进行处理
• 
• 简单变形优化
• 
• 防止整型溢出优化
• 
• 具体代码实现
• 

4.. 复合类型哈希函数的设计

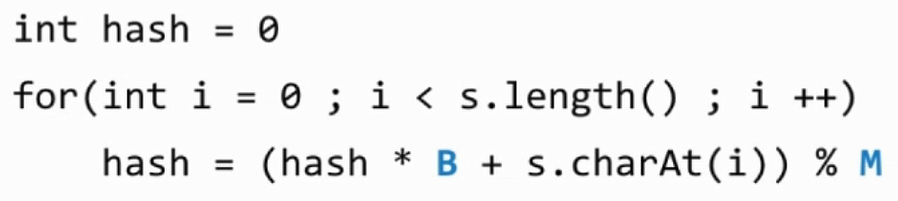
• 转成整型进行处理
• 

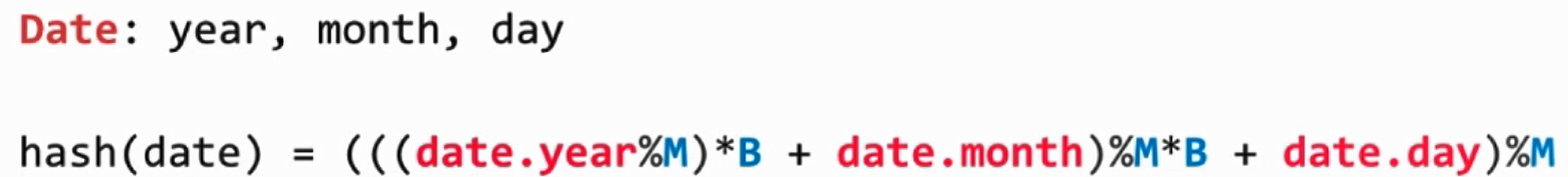
5.. 哈希函数的设计原则

• 

6.. 哈希冲突的处理

• 链地址法
• 
• 开放地址法之线性探测
• 

• 开放地址法之平方探测

• 
• 开放地址法之二次哈希
• 

7.. 哈希表的动态空间处理

• 

8.. 实现哈希表的业务逻辑

• import java.util.TreeMap;
  
  public class HashTable<K, V> {
  
      private final int[] capacity
              = {53, 97, 193, 389, 769, 1543, 3079, 6151, 12289, 24593,
              49157, 98317, 196613, 393241, 786433, 1572869, 3145739, 6291469, 12582917,
              25165843, 50331653, 100663319, 201326611, 402653189, 805306457, 1610612741};
      private static final int upperTol = 10;
      private static final int lowerTol = 2;
      private int capacityIndex = 0;
      private TreeMap<K, V>[] hashTable;
      private int M;
      private int size;
  
      public HashTable() {
  
          this.M = capacity[capacityIndex];
          this.size = 0;
          hashTable = new TreeMap[M];
          for (int i = 0; i < M; i++) {
              hashTable[i] = new TreeMap<>();
          }
      }
  
      private int hash(K key) {
          return key.hashCode() & 0x7fffffff % M;
      }
  
      public void add(K key, V value) {
  
          TreeMap<K, V> map = hashTable[hash(key)];
  
          if (map.containsKey(key)) {
              map.put(key, value);
          } else {
              map.put(key, value);
              size++;
              if (size >= upperTol * M && capacityIndex + 1 < capacity.length) {
                  capacityIndex++;
                  resize(capacity[capacityIndex]);
              }
          }
      }
  
      public V remove(K key) {
  
          TreeMap<K, V> map = hashTable[hash(key)];
  
          V ret = null;
          if (map.containsKey(key)) {
              ret = map.remove(key);
              size--;
              if (size < lowerTol * M && capacityIndex - 1 >= 0) {
                  capacityIndex--;
                  resize(capacity[capacityIndex]);
              }
          }
          return ret;
      }
  
      public void set(K key, V value) {
  
          TreeMap<K, V> map = hashTable[hash(key)];
  
          if (!map.containsKey(key)) {
              throw new IllegalArgumentException(key + "doesn't exist.");
          } else {
              map.put(key, value);
          }
      }
  
      public boolean contains(K key) {
  
          return hashTable[hash(key)].containsKey(key);
      }
  
      public V get(K key) {
  
          return hashTable[hash(key)].get(key);
      }
  
      private void resize(int newM) {
  
          TreeMap<K, V>[] newHashTable = new TreeMap[newM];
          for (int i = 0; i < newM; i++) {
              newHashTable[i] = new TreeMap<>();
          }
  
          int oldM = M;
          M = newM;
          for (int i = 0; i < oldM; i++) {
              TreeMap<K, V> map = hashTable[i];
              for (K key : map.keySet()) {
                  newHashTable[hash(key)].put(key, map.get(key));
              }
          }
  
          this.hashTable = newHashTable;
      }
  
  }