九度OJ小结

1. 高精度问题

　　可参考题目 题目1137：浮点数加法   http://ac.jobdu.com/problem.php?pid=1137

　　对于高精度问题可以考虑使用结构体。上述为浮点数加法，因此该结构体可以具有保存小数部分以及整数部分的成员变量，使用数组进行保存。于此同时还要记录下所保存数据的长度，因此还应当有两个int变量，保存整数部分长度和保存小数部分长度。

在C++中对运算符进行重载操作。

运算符函数定义的一般格如下所示：

<返回类型说明符> operator <运算符符号>(<参数表>)
{

     <函数体>

}

成员函数运算符

运算符重载为类的成员函数的一般格式为：
<函数类型> operator <运算符>(<参数表>)

    {

     <函数体>

    }
  () 双目运算符重载为类的成员函数时，函数只显式说明一个参数，该形参是运算符的右操作数。

() 前置单目运算符重载为类的成员函数时，不需要显式说明参数，即函数没有形参。

() 后置单目运算符重载为类的成员函数时，函数要带有一个整型形参。

    调用成员函数运算符的格式如下：

    <对象名>.operator <运算符>(<参数>)  它等价于  <对象名><运算符><参数>

      例如：a+b等价于a.operator +(b)。一般情况下，我们采用运算符的习惯表达方式。

运算符重载为类的友元函数的一般格式为：

    friend <函数类型> operator <运算符>(<参数表>)

    {

     <函数体>

    }

当运算符重载为类的友元函数时，由于没有隐含的this指针，因此操作数的个数没有变化，所有的操作数都必须通过函数的形参进行传递，函数的参数与操作数自左至右一一对应。

　调用友元函数运算符的格式如下：

    operator <运算符>(<参数1>,<参数2>)

    它等价于

    <参数1><运算符><参数2>

    例如：a+b等价于operator +(a,b)。

两种重载形式的比较

　　在多数情况下，将运算符重载为类的成员函数和类的友元函数都是可以的。但成员函数运算符与友元函数运算符也具有各自的一些特点：

() 一般情况下，单目运算符最好重载为类的成员函数；双目运算符则最好重载为类的友元函数。

() 以下一些双目运算符不能重载为类的友元函数：=、()、[]、->。

() 类型转换函数只能定义为一个类的成员函数而不能定义为类的友元函数。

() 若一个运算符的操作需要修改对象的状态，选择重载为成员函数较好。

() 若运算符所需的操作数（尤其是第一个操作数）希望有隐式类型转换，则只能选用友元函数。

() 当运算符函数是一个成员函数时，最左边的操作数（或者只有最左边的操作数）必须是运算符类的一　个类对象（或者是对该类对象的引用）。如果左边的操作数必须是一个不同类的对象，或者是一个内部　类型的对象，该运算符函数必须作为一个友元函数来实现。

() 当需要重载运算符具有可交换性时，选择重载为友元函数。

重载操作解析

对于浮点数加法而言，结果的输出需要注意前导0的消除。

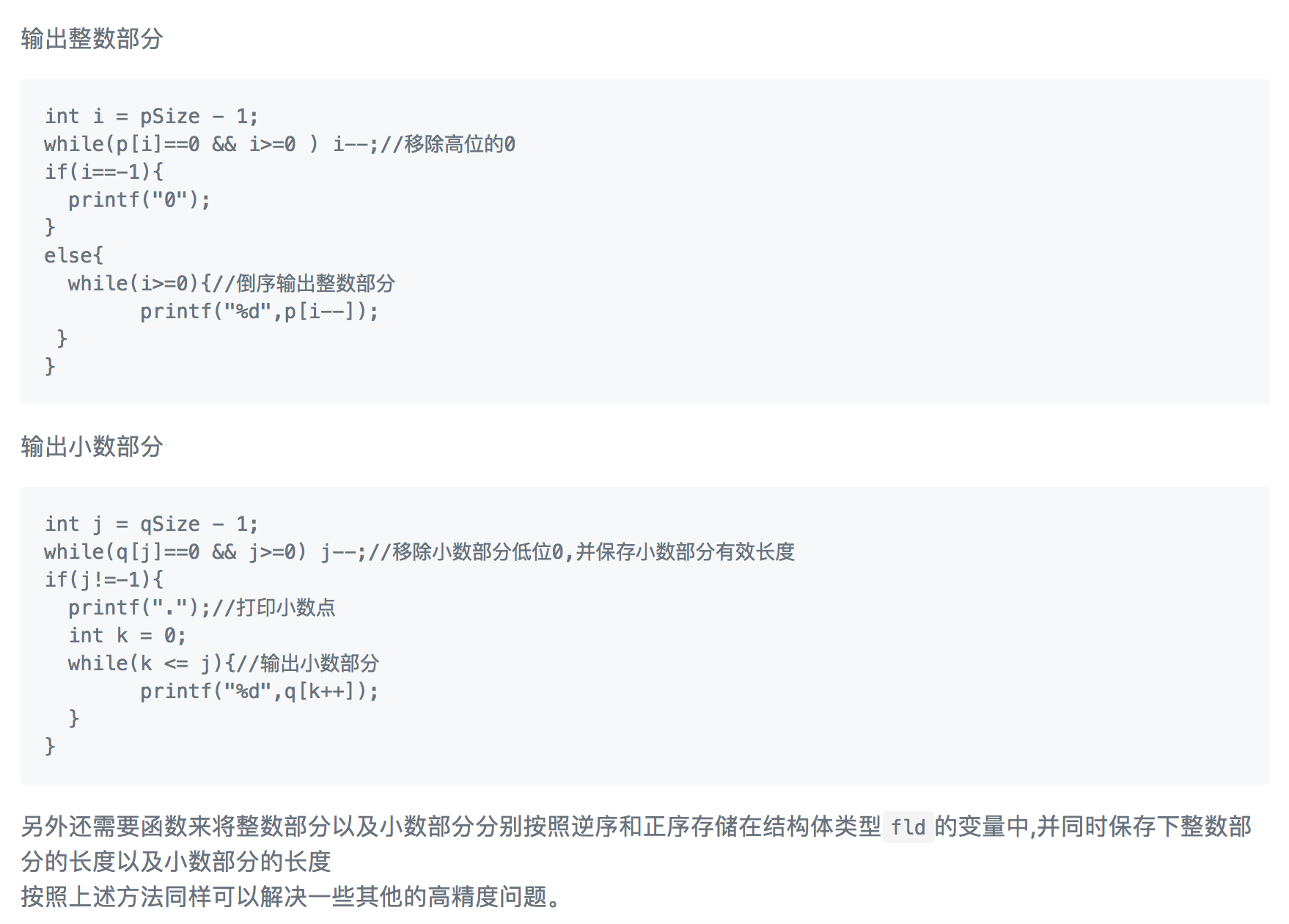
2. 进制转换问题

     可参考题目 题目1080：进制转换 http://ac.jobdu.com/problem.php?pid=1080 

     对于进制转换问题，通过博客http://blog.csdn.net/jaster_wisdom/article/details/52107785 进一步了解具体的方法。

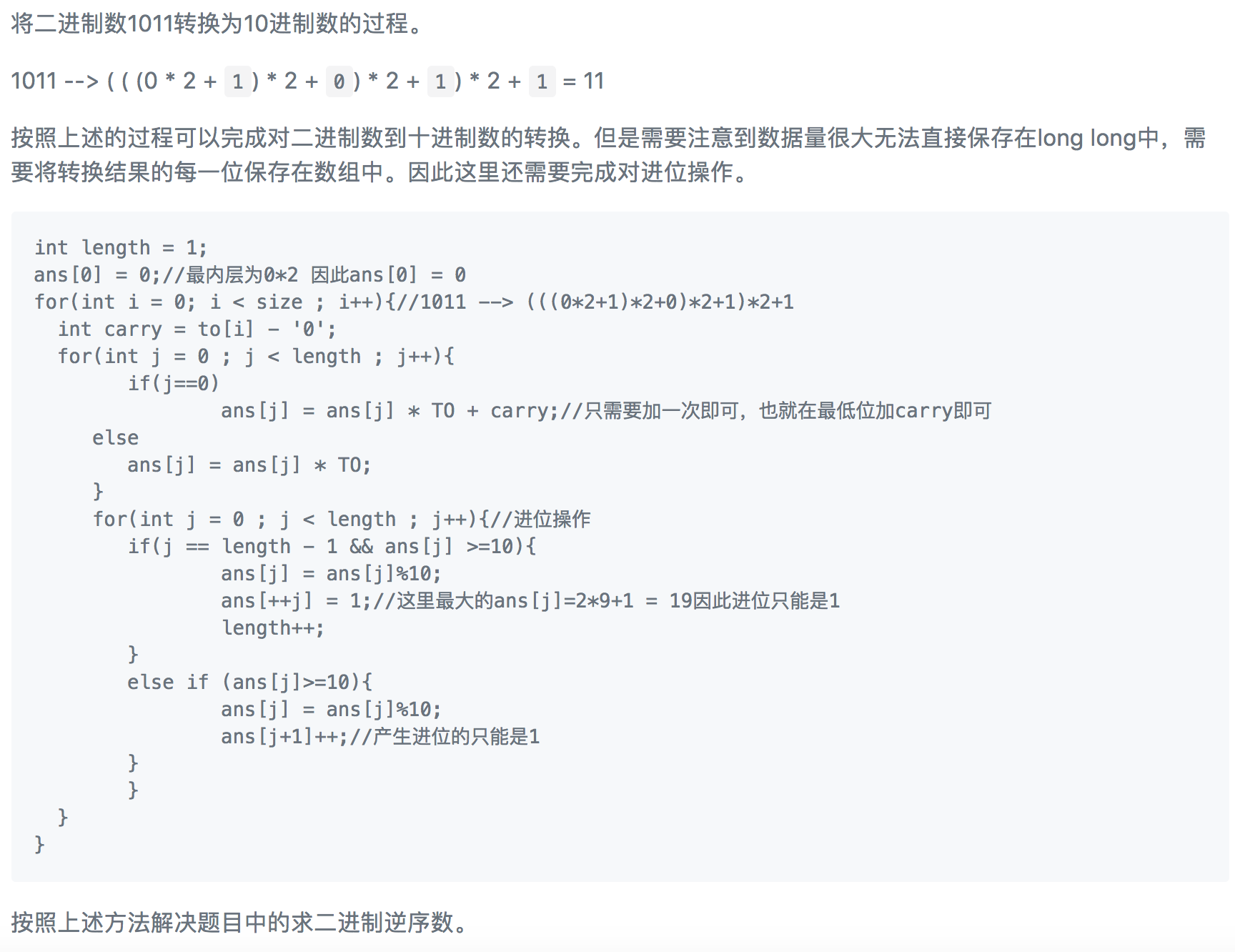
     其中的方法算是从笔算转换进制转化来的，但是这个笔算的过程有那么点复杂。如果仅仅是举一个10进制到2进制的转换，其中的规律好像不是很清晰。需要注意的是在其他进制转换过程中向下余数不再是10倍的关系而是原来进制m的倍数，同时除数是进制n。

     按照上述的笔算方法，得到的进制结果依次是从最低位到最高位。也就是保存的结果如果需要输出的话，应该倒序输出。

     另外对于题目  题目1208：10进制 VS 2进制  http://ac.jobdu.com/problem.php?pid=1208 

      需要考虑大数的保存问题以及进位操作。

　　

       需要注意的是这里的进位只有加1操作，因为是10进制转2进制。如果是其他进制的话，需要使用 ans[j]%n(n为转换目标进制)

       

       这里说到了大数问题，这里的N的阶乘问题也顺带提一下。

       可参考题目  题目1076：N的阶乘   http://ac.jobdu.com/problem.php?pid=1076

      

3. 二分求幂问题

      计算pow(n,k) = n^k 可参考题目  题目1441：人见人爱 A ^ B http://ac.jobdu.com/problem.php?pid=1441

      将k按照二进制展开，按照从二进制最低位到最高位进行幂乘操作。

      

 4. 大整数排序问题

      可参考题目 题目1190：大整数排序 http://ac.jobdu.com/problem.php?pid=1190

 

        无符号大整数进行非递减排序时，可以通过比较长度决定数字的大小。如果长度相同，那么可以调用函数strcmp函数

　　  设这两个字符串为str1，str2，若str1==str2，则返回零；若str1<str2，则返回负数；若str1>str2，则返回正数。

　　  另外在保存大整数的时候采用二维char数组。

        这里的排序可以采用qsort，需要手写cmp函数。

　　  其中本题目的函数模型如下所示：

int cmp(const void *a, const void *b){
    int lena = (int)strlen((char *)a);
    int lenb = (int)strlen((char *)b);
    if(lena == lenb)
        return strcmp((char *)a, (char *)b);
    else
        return lena < lenb;
} 

另外对于qsort函数的其他模板可以参考博客  http://blog.csdn.net/yuanjilai/article/details/7348345

 5. 并查集操作问题

 

     九度 OJ1012 畅通工程   http://ac.jobdu.com/problem.php?pid=1012

      九度 OJ1109 连通图; http://ac.jobdu.com/problem.php?pid=1109

      九度 OJ1445 How Many Tables?; http://ac.jobdu.com/problem.php?pid=1445

      九度 OJ1444：More is better  http://ac.jobdu.com/problem.php?pid=1444

      九度 OJ1446 Head of a Gang;  http://ac.jobdu.com/problem.php?pid=1446

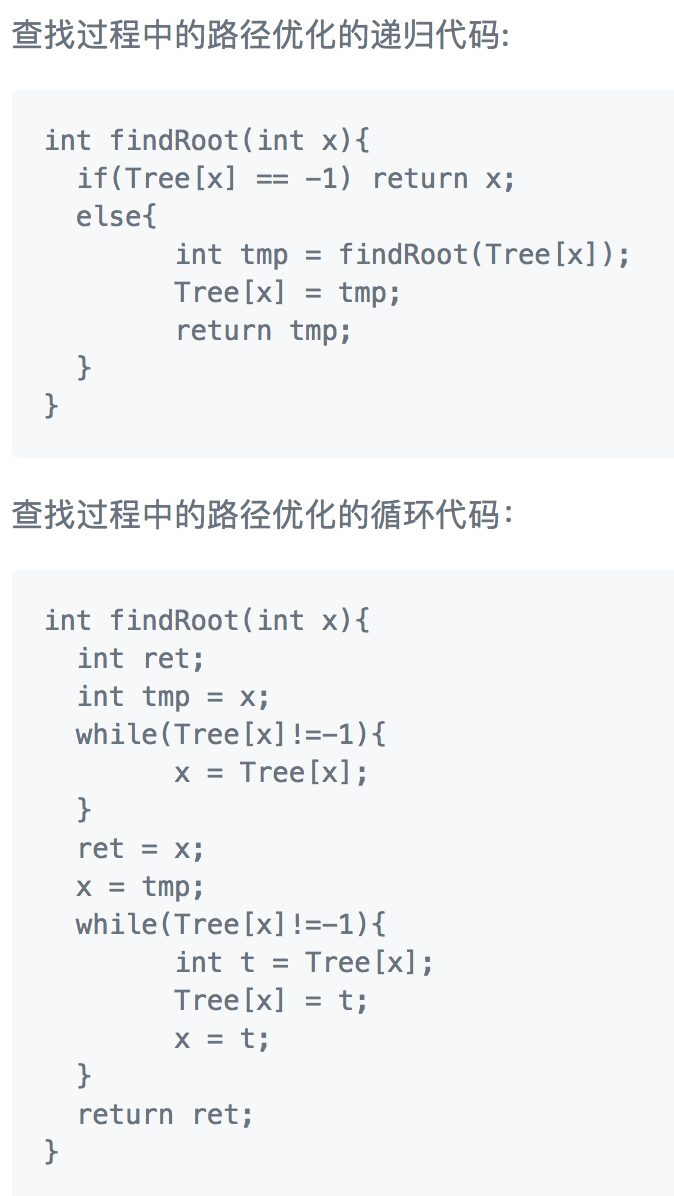
对于1446需要考虑的问题有并查集问题，姓名与Id对应问题（使用map存储），条件判断等问题。

可以参考博客 http://blog.csdn.net/u013027996/article/details/17101513 

         OJ1446 基本思路：
        1、如果要使用数组，需要将字母转换为数字，当然最后输出的时候要转换回去。
         2、并查集，读取两个name的时候，就合并。
         3、求父节点，并且算出集合个数。
         4、对每个集合做计算，求成员个数。符合条件，保留，不符合条件，忽略。
         5、按照字母序输出结果。