Matlab学以致用 - 曲线拟合

曲线拟合

使用Matlab自带的polyfit函数，可以很方便地根据现有样本数据进行多项式曲线拟合，为了有直观感受，先上例程，如下所示：

 x = -:0.1:;                           % 样本数据x坐标
 y = *x.^ + *x +  + randn(size(x));  % 样本数据y坐标，添加随机噪声

 p = polyfit(x, y, );   % 使用自带函数进行数据拟合，拟合的多项式维数n=
 yy = polyval(p, x);     % 生成拟合数据

 figure, plot(x, y, '.');                    % 显示原始数据
 xlabel('x'), ylabel('y');                   % 坐标轴
 hold on, plot(x, yy, 'r', 'LineWidth', );  % 显示拟合数据
 legend('raw data', 'fitting line');         % 图例

运行结果：

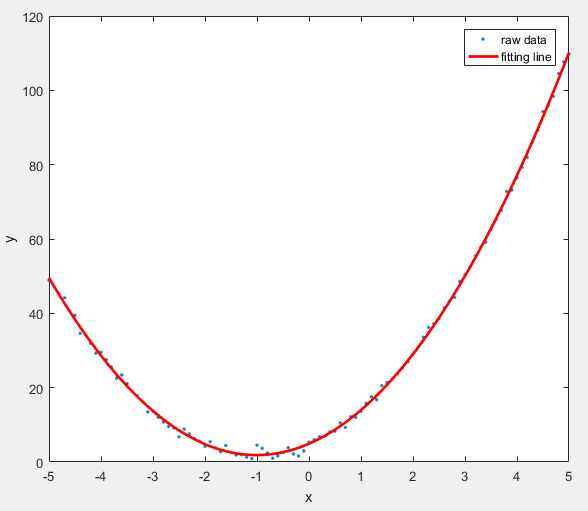
函数说明：
p = polyfit(x,y,n) returns the coefficients for a polynomial p(x) of degree n that is a best fit (in a least-squares sense) for the data in y. The coefficients in p are in descending powers, and the length of p is n+1

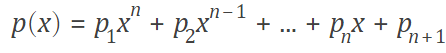
即，polyfit(x,y,n) 返回对应于样本数据y的n维多项式p(x)的系数（基于最小二乘法）。该系数按照降幂顺序排列，个数为 n+1

---

直线拟合

基本原理：给定一组数据[x1,x2,…,xn]和[y1,y2,…yn]，已知x和y成基本线性关系，即存在一条最佳拟合直线 y = kx + b，对此，同样可以基于最小二乘法来求出系数k和b。此时，调用polyfit(x,y,n)时，应取n=1，即把直线拟合看作是一阶多项式的拟合，在此不再赘述。

另外，还可以使用基于矩阵除法的直线拟合方法，基本原理如下：

例程：

 % 基于矩阵除法的直线拟合
 x = [0.5  1.5  2.5 ];
 y = [1.75 2.45 3.81 4.8  8.6];  

 n = length(x);
 x = reshape(x,n,);          % 生成列向量
 y = reshape(y,n,);
 A = [x,ones(n,)];           % 连接矩接A  

 yy = A \ y;                  % 左除，相当于inv(A)*y

 k = yy();                   % 得到k
 b = yy();                   % 得到b

 yy = polyval([k, b], x);     % 生成拟合数据
 figure,
 plot(x, y, '*');
 hold on, plot(x, yy, 'r');   % 显示拟合曲线

运行结果：

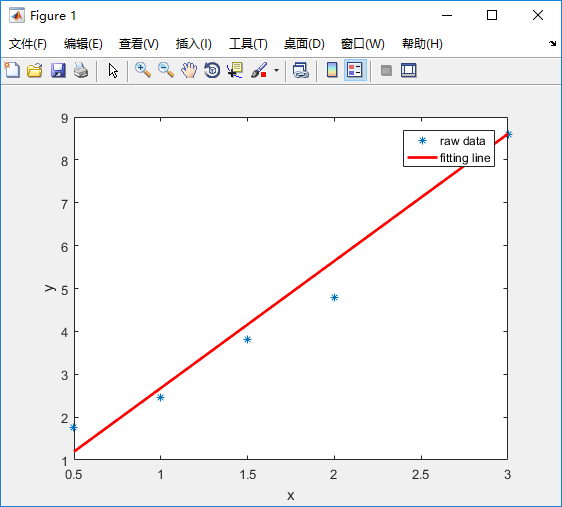
reference

• http://cofftech.iteye.com/blog/2211239
• http://blog.csdn.net/seamanj/article/details/36209865