HDU 6070 Dirt Ratio（分数规划+线段树）

http://acm.hdu.edu.cn/showproblem.php?pid=6070

题意：

找出一个区间，使得（区间内不同数的个数/区间长度）的值最小，并输出该值。

思路：

因为是要求$\frac{f(x)}{g(x)}$的最值，所以这是分数规划的题目，对于分数规划，是要用二分查找的方式去解决的。

就像官方题解说的，二分查找mid，二分答案mid，检验是否存在一个区间满足$\frac{size(l,r)}{(r-l+1)}<=mid$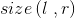，表示l~r内不同数的个数。

先把上面的式子转化一下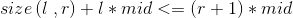，，用线段树维护区间内不同数的个数，因为l*mid是固定值，所以把它也可以加进去，这样线段树就维护了区间内不等式左边的最小值。

从左到右枚举r，先是在pre[a[r]]+1~r这段区间内将区间值+1，因为这段区间内a[r]并没有出现过。更新完了之后就查询，因为线段树内记录的就是不等式左边的最小值，所以就可以返回最小值然后判断是否小于等于（r+l）*mid。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<sstream>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,int> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn=1e6+;
 const int mod=;
 const double eps=1e-;

 int n;
 double now;
 int a[maxn];
 int pre[maxn];
 double add[maxn<<];
 double sum[maxn<<];

 void PushUp(int o)
 {
     sum[o]=min(sum[o<<],sum[o<<|]);
 }

 void PushDown(int o)
 {
     if(add[o])
     {
         add[o<<]+=add[o];
         add[o<<|]+=add[o];
         sum[o<<]+=add[o];
         sum[o<<|]+=add[o];
         add[o]=;
     }
 }

 void build(int l, int r, int o)
 {
     sum[o]=add[o]=;
     if(l==r)
     {
         sum[o]=l*now;
         return ;
     }
     int mid=(l+r)>>;
     build(l,mid,o<<);
     build(mid+,r,o<<|);
     PushUp(o);
 }

 void update(int ql, int qr, int l, int r, int x, int o)
 {
     if(ql<=l && qr>=r)
     {
         sum[o]+=x;
         add[o]+=x;
         return;
     }
     PushDown(o);
     int mid=(l+r)>>;
     if(mid>=ql)   update(ql,qr,l,mid,x,o<<);
     if(mid<qr)    update(ql,qr,mid+,r,x,o<<|);
     PushUp(o);
 }

 double query(int ql, int qr, int l, int r, int o)
 {
     if(ql<=l && qr>=r)
     {
         return sum[o];
     }
     PushDown(o);
     double ans=INF;
     int mid=(l+r)>>;
     if(mid>=ql)   ans=min(ans,query(ql,qr,l,mid,o<<));
     if(mid<qr)    ans=min(ans,query(ql,qr,mid+,r,o<<|));
     return ans;
 }

 bool check()
 {
     memset(pre,,sizeof(pre));
     build(,n,);
     for(int i=;i<=n;i++)
     {
         double tmp=now*(i+1.0);
         update(pre[a[i]]+,i,,n,,);
         if(query(,i,,n,)<=tmp)  return true;
         pre[a[i]]=i;
     }
     return false;
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d",&n);
         for(int i=;i<=n;i++)  scanf("%d",&a[i]);

         double l=,r=;
         double ans;
         while(r-l>=eps)
         {
             double mid = (r+l)/2.0;
             now = mid;
             if(check())
             {
                 ans=mid;
                 r=mid-eps;
             }
             else l=mid+eps;
         }
         printf("%.9lf\n",ans);
     }
     return ;
 }