MIT-线性代数笔记（7-11）

第 07 讲求解 Ax=0 :主变量，特解

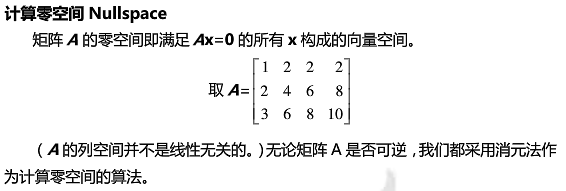
矩阵的秩Rank(A)：矩阵主元的个数。

找出“主变量”pivotvariables，主列，即主元所在的列，其他列，称为自由列。（自由列表示可以自由或任意分配数值，列2和列4的数值是任意的，因此x2和x4是任意的，可以自由取）。

算法整理：

消元后矩阵U的秩Rank(A)=r，表示主变量的个数，主元的个数，表示只有r个方程起作用，那么自由变量的个数即n-r个（对于矩阵m×n，n列对应n个未知数），令自由变量取1,0值就能得到特解，所有的特解构成了零空间的基，特解的线性组合即构成了整个零空间。

简化行阶梯形式
R=简化行阶梯形式reducedrowechelonform（rref）：主元上下都是0，主元变为1

它以最简的形式包含了所有信息：1）主行（行一，行二）；
2）主列（列一，列三），自由列，主元；
3）一个单位阵，主元上下均为0，而且主元为1，单位阵位于主列和主行的交汇处。以上是一个2×2的单位阵；
4）一个全为0的行，全为0的行总表示，该行的原行是其他行的线性组合；5）从Ax=0变为Ux=0再变为Rx=0的解，解更明了

将以上矩阵R中的主元列和自由列分别放在一起形成单位矩阵I和自由列矩阵F，对于特解结果，自由列中数字的相反数即特解中的主元值，如下图左边的解和右边的I与F

第 08 讲求解 Ax=b：可解性与结构

若 Ax=b 有解，则 b3-b1-b2=0

Ax=b可解性Solvability：有解时右侧向量b须满足的条件
1）有解，仅当b属于A的列空间时成立，即，b必须是A的各列的线性组合

2）行的线性组合如果得到零行，那么b中元素的同样组合必然也是零。这两种描述是等价的！他们同样是描述方程组有解的条件。

把所有这些解在四维空间中都画出来，想象一下，Xp是一个非原点的点，Xn是一个穿过原点的平面，那么Xp+Xn是两者的组合，是一个不经过原点的经过Xp的二维平面，注意它不是子空间。

第 09 讲线性相关性、基、维数

基

向量空间的一组基是指：一系列的向量，v1,v2...vd，这些向量具有两大性质：1）他们是线性无关的，可逆；2）他们生成整个空间

这些基有一个共同的特点，即对于给定N维空间，那么基向量的个数就是N个（即不管是3维空间，列空间，还是零空间，空间中任意基都满足：基向量的个数相等）。

维数
维数，即基向量的个数，空间的大小(维数)

比如上面这个列向量，他们能生成列空间，但这些列向量不是基，但我们可以得到第一列和第二列是列空间的一组基，2是基的维数。
即上面：矩阵的秩Rank(A)=2为列空间的维数（注意不是矩阵A的维数，是A的列空间的维数，同样，不能说子空间的秩，矩阵才有秩）。

零空间的维数是自由变量的数目。已知矩阵Am×n，秩为r，那么自由变量为n-r，即dim(N(A))=n-r

第 10 讲四个基本子空间

维数问题
列空间：

　　A的主列就是列空间的一组基，dim(C(A))=Rank(A)=r，维数就是秩的大小行空间：有一个重要的性质：行空间和列空间维数相同，都等于秩的大小
零空间：

　　一组基就是一组特殊解，r是主变量的个数，n-r是自由变量的个数，零空间的维数等于n-r左零空间：维数为m-r。

　　n维空间中存在两个子空间，一个r维的行空间，一个n-r维的零空间，维数和为n。和另一个结论相似：r个主变量，n-r个是自由变量，加起来是n。
　　m维空间中存在两个子空间，一个r维的列空间，一个m-r维的左零空间，维数和为m。

　　左零空间的基

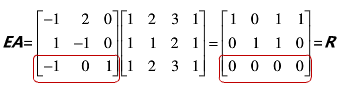
基的问题

列空间：主列组合就是一组基
零空间：一组特殊解就是一组基
行空间：通过初等行变换变换成行最简式，行空间的一组基即是行最简形R的前r(秩数)行。（行变换不会对行空间产生影响，但会对列空间产生影响。）

新向量空间

　　所有3*3矩阵构成的集合是一个向量空间，符合对于现行运算的封闭，称之为M

　　M的子空间包括：

所有上三角阵
所有对称阵
所有对角阵

　　对角阵是前两个子空间的交集，维数为3，具有以下一组基：

第 11 讲矩阵空间、秩1矩阵和小世界图

3×3的所有矩阵，它的维数是9，一组基是：

秩1矩阵
回到重点，矩阵的关键数字——矩阵的秩，秩为1的矩阵
所有秩1的矩阵都可表示为一列乘以一行的形式：A=UVT，U是列向量，V也是列向量
秩1矩阵可以就像搭建其他矩阵的积木一样，如果有5×17的矩阵，秩为4，可以把这5×17的矩阵分解为4个秩1矩阵的组合。

两个矩阵之和的秩小于等于两个矩阵的秩之和