15分钟理解HTTPS——通俗篇

| 导语 它很深奥吗？你肯定常常见过它，使用它，甚至离不开它... 它很浅显吗？你可能觉得看透它，理解它，甚至懂它... 让我们用15分钟，不那么学术地将它的深挖到底~

什么？如何证明我是我？本文要上升到这样的哲学高度了吗？吓得作者笔都掉了，不，是键盘按键都飞出来了…

HTTPS的身份认证机制还真的是一个“如何证明我是我”的问题，并且巧妙地使用了“零知识证明”。先来看个故事吧！

我知道某带密码门锁房间的密码，如何证明我有这个密码呢？下面有两种方式：

①我把密码告诉你，你用密码打开该房间的锁。

②我们都知道房间内有某一物体，我用密码打开房间的门，然后把物体拿出来给你看。

方式①的结果是密码泄漏了，如果换作二战被俘的情报员或者被四十大盗劫持的阿里巴巴身上，他们的结局一定是被无情杀害了。

方式②是零知识证明。它指的是证明者能够在不向验证者提供任何有用的信息的情况下，使验证者相信某个论断是正确的。

那下面我们来挖一挖HTTPS如何借鉴这种思想进行身份认证的。不过，先来看一眼目录吧！没有目录的长文都是耍流氓…

1.HTTPS原理概述

1.1什么是HTTPS？

1.2HTTPS保证安全通信的原理（加密|签名|证书）

1.3一次完整的HTTPS过程

2.HTTPS实践与应用

2.1从HTTP升级到HTTPS

2.2Fiddler抓包HTTPS

2.3局限性和使用场景

1.1什么是HTTPS？

一句话：超文本传输安全协议（Hypertext Transfer Protocol Secure, HTTP）是在应用层和传输层中间多了安全层的HTTP协议。安全层协议是SSL或者TLS。

为什么要有HTTPS呢？因为HTTP通信是明文传输，有以下风险，而HTTPS完美地解决了这些风险。

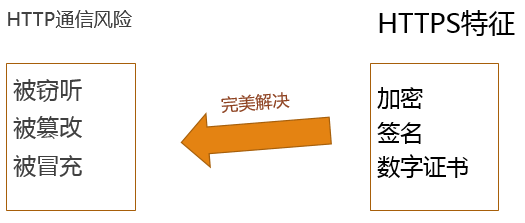
1.2HTTPS保证安全通信的原理

（一） 
加密——防窃听

举一个最简单的加密，abc->bcd。

l  加密函数f：将加密过程抽象成函数。

l  密钥： f(n)中的参数n。上例中n=1。

l  对称加密：加密和解密的密钥相同。计算量小，速度快。

l  非对称加密：加密和解密的密钥不同，一般地，服务器方存有私钥不外传，而把对应公钥开放给客户端。客户端用公钥加密内容，服务器用私钥解密。计算量大，速度慢。

HTTPS的真正加密过程：用非对称加密方式协商对称密钥；通信时使用协商好的对称密钥。这段话在看完1.3会更加清晰。

对称加密非常好理解。HTTPS关键技术之一的非对称加密是如何实现的呢？以比较具有代表性的RSA算法为例，解剖下非对称加密实现原理：

首先，存在这样一个事实（1）。其次，非对称加密是公钥私钥计算过程大致如（2）所述。然后，（3）利用两个式子可以进行加密和解密。

那么，RSA实现非对称加密的原理问题，可以简化为（3）中两个式子的m是否相等。将(1)中的等式带入（3）中公式，加以不长不短的数学证明，结果显示两式相等。Done! 总结来说，RSA的实现基于的是数学世界中存在的两个质数之间不对称关系。（文末附有证明的参考资料）

(1)两个互质数之间存在一个等式

如果两个正整数a和n互质，那么一定可以找到整数b，使得 ab-1 被n整除，或者说ab被n除的余数是1。这时，b就叫做a的“模反元素”。这个等式可以由“欧拉定理”证明。

(2)利用这两个互质数产生一对公钥私钥

S1.随机选择两个不相等的质数p和q。

S2.计算p和q的乘积n。

S3.计算n的欧拉函数φ(n)。

S4.随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质。

　　S5.计算e对于φ(n)的模反元素d。

　　S6.（n,e）是公钥，（n,d）是私钥。

(3)加密和解密

加密：m是要加密信息，用(n,e)计算出加密后信息c。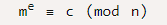

解密：用(n,d)计算出原始信息m。

（二） 
签名——防篡改

签名如何证明信息没有被纂改？

举例子：

开发gg小猴很帅，到处发自己的公钥给妹子。有一天他中意一个妹子，想私下给妹子加密写信。为了防止信被他的好哥们乱改，他这样做：

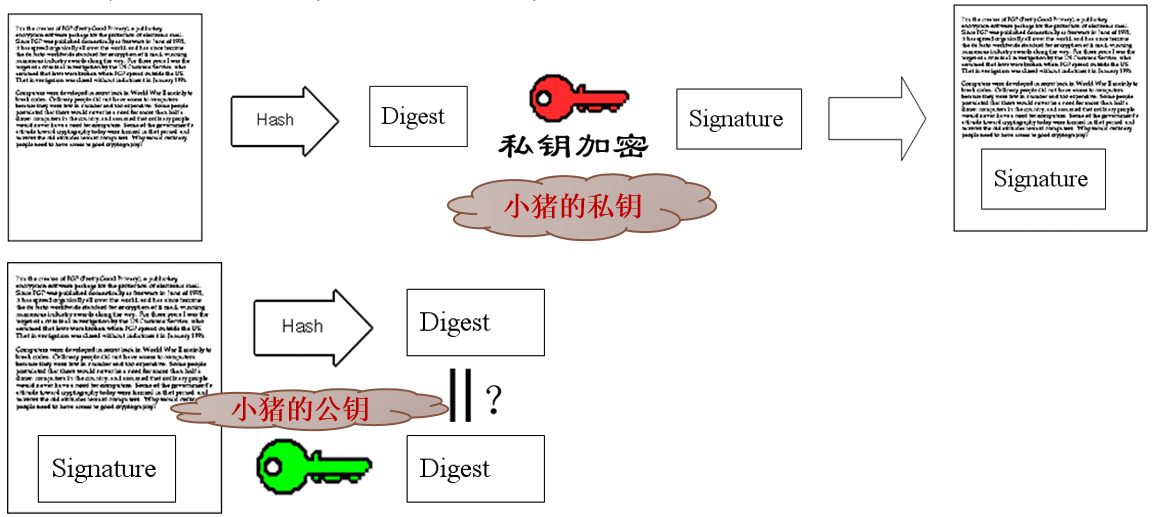
把信的内容哈希得到摘要，摘要进行私钥加密得到签名，签名附到信后面。

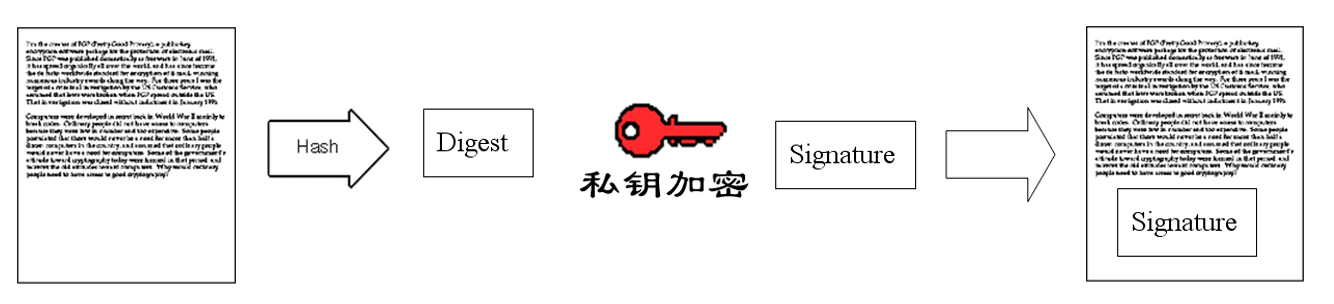
妹子收到了信，熟练地把信内容哈希得到摘要，把签名公钥解密得到摘要，对比两个摘要相同，相信了这信没被别人纂改过。防止篡改的原理就是，外人只改动内容会对不上签名中的摘要，而签名又是加密过的无法和内容修改的一致。

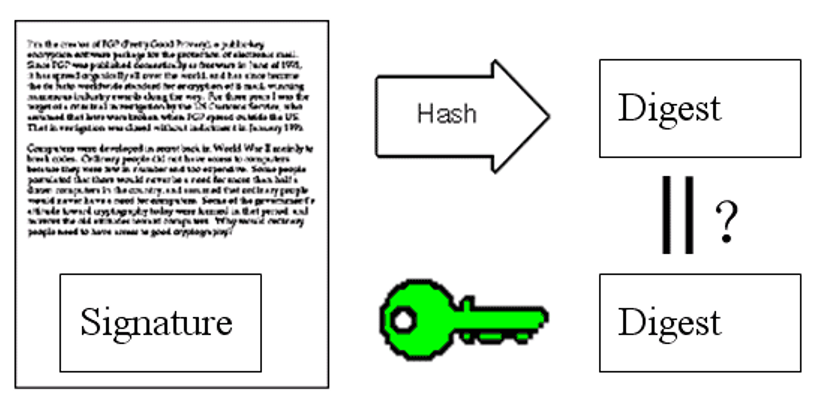
（三）  证书——防冒充

可惜，妹子还是套路不够深….

小猴的哥们小猪也喜欢这个妹子，不敢表白，偷偷冒充了小猴。

他盗用小猴电脑，把小猴公钥换成自己公钥，用自己的私钥给妹子写信。

妹子以为自己拿着小猴的公钥，验证了信没被纂改过。而实际上这公钥是小猪的，信也是小猪写的。

要避免这样的悲剧，“数字证书”就出场了。既然无法确信“小猴的公钥是小猴的“，那只好找权威机构帮忙认证了

小猴去证书中心(CA)申请证书，CA用自己的私钥对小猴的公钥和相关信息一起加密，生成“数字证书“。小猴再写信时，附上签名和证书。

妹子收到信，用CA的公钥(这个不好冒充)解密证书，确信得到的是小猴的公钥了。

再来看开始提到的零知识证明。它的一个应用是Guillo-Ouisquater身份认证，这种认证方式主要基于了RSA公钥算法的基本思想。换句话说，前述的签名和证书的身份认证属于零知识证明的应用。过程需要一个权威CA，认证可靠，并没有提供任何有用信息，也不会因认证次数增加而安全性降低。

1.3一次完整的HTTPS过程

流程概述：

1. 客户端向服务器索要公钥，并验证
2. 双方协商生成对话密钥（对称加密）
3. 采用对称加密通信

步骤1和2称为握手过程。

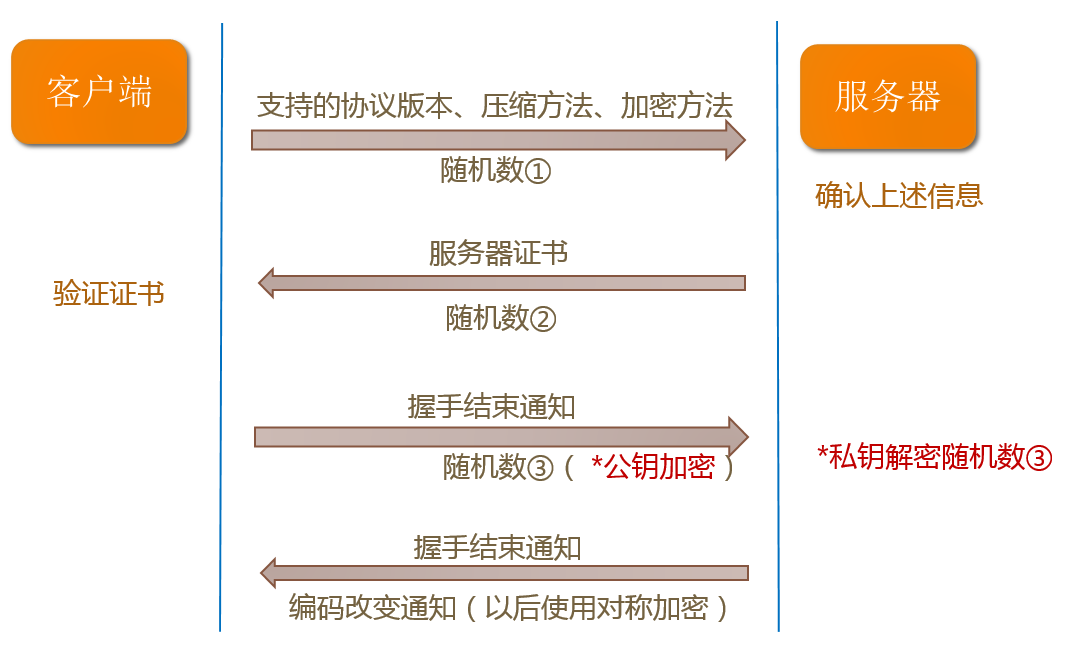
验证证书时，浏览器一般存有大型可信CA的公钥。验证证书是否为真，是否过期等。如验证不通过，浏览器会显示警告，用户可以选择继续访问。

至此，客户端和服务都有了随机数①②③，用它们三个形成相同的对称密钥，用于接下来通信。

Session恢复：

如果出于某种原因，对话中断，就需要恢复对话。

Ø  Session ID：session
ID保存在一台服务器中，如果客户端能提供上次的session ID，就不再需要重新握手。

Ø  Session ticket：不局限于一台服务器， session ticket是上次对话中服务器发送的，内容是加密过的密钥和解密方法等，客户端如果能提供session ticket，也可以恢复对话。

2.HTTPS实践与应用

2.1从HTTP升级到HTTPS

1申请证书

认证级别

ü  域名认证：最低级别认证，可以确认申请人拥有这个域名。对于这种证书，浏览器会在地址栏显示一把锁。

ü  公司认证：确认域名所有人是哪一家公司，证书里面会包含公司信息。

ü  扩展认证：最高级别的认证，浏览器地址栏会显示公司名。

证书类型

Ø  单域名证书：只能用于单一域名，foo.com的证书不能用于www.foo.com

Ø  通配符证书：可以用于某个域名及其所有一级子域名，比如*.foo.com的证书可以用于foo.com，也可以用于www.foo.com

Ø  多域名证书：可以用于多个域名，比如foo.com和bar.com

2证书安装和配置

一般地，这部分工作会被运维的同事做。

3修改链接

通常直接去掉协议名称，根据用户输入的协议为准。如：//vip.qq.com

当用户使用http请求时还是不走https，这时还可以：

不修改链接，修改web服务器配置，使用301重定向，如

server {

listen 80;

server_name domain.com www.domain.com;

return 301 https://domain.com$request_uri;

}

2.2Fiddler抓包HTTPS

1.开启fiddler支持https抓包

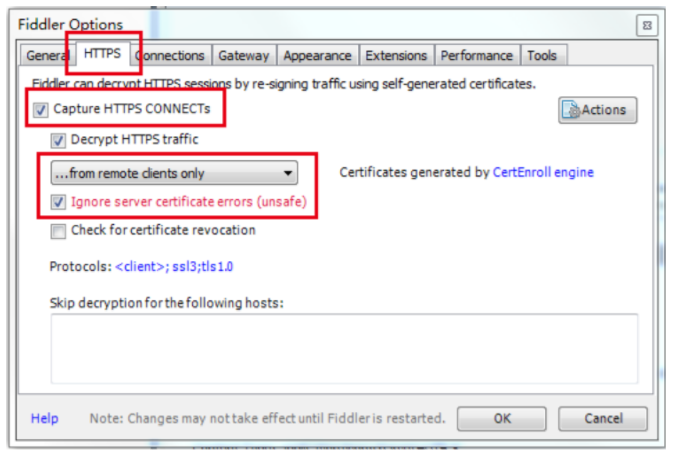
2.访问fiddler代理IP：端口，点击安装证书

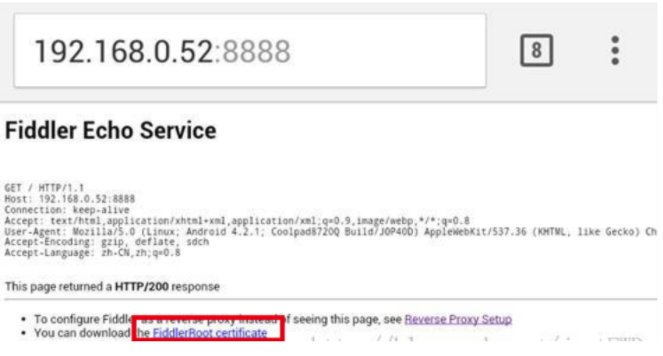
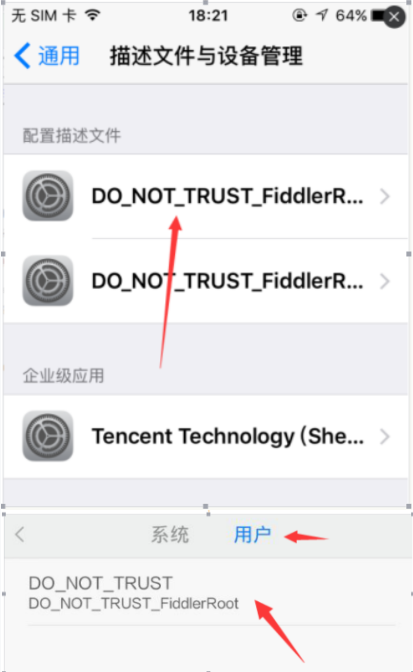
3.对证书授信

Ø  ios：设置-通用-描述文件与设备管理-点进去选择信任

Ø  android：设置-安全和隐私-受信任的凭据-用户-点进去选择信任

2.3HTTPS的局限性和使用场景

https由于过程复杂，耗时稍慢，需要证书等因素，使得需要高安全性的网站才应用它，或者只在注、登陆、支付等关键页面才使用。

但https如果经过优化，不会明显影响性能，所有场景都适合使用。

参考资料

《RSA算法原理（一）》

http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html

《RSA算法原理（二）》

http://www.ruanyifeng.com/blog/2013/07/rsa_algorithm_part_two.html

《数字签名是什么？》

http://www.ruanyifeng.com/blog/2011/08/what_is_a_digital_signature.html

https://wenku.baidu.com/view/5cf354fd31b765ce04081463.html

https://wenku.baidu.com/view/88a0f233eefdc8d376ee328e.html

《SSL/TLS协议运行机制的概述》

http://www.ruanyifeng.com/blog/2014/02/ssl_tls.html

《图解SSL/TLS协议》

http://www.ruanyifeng.com/blog/2014/09/illustration-ssl.html

《HTTPS 升级指南》

http://www.ruanyifeng.com/blog/2016/08/migrate-from-http-to-https.html

等...