Algorithm --> 矩阵链乘法

动态规划--矩阵链乘法

1、矩阵乘法

　

　　

 

 

 

Note：只有当矩阵A的列数与矩阵B的行数相等时A×B才有意义。一个m×r的矩阵A左乘一个r×n的矩阵B，会得到一个m×n的矩阵C。

#include <iostream>
using namespace std;
#define A_ROWS        3
#define A_COLUMNS     2
#define B_ROWS        2
#define B_COLUMNS     3
void matrix_multiply(int A[A_ROWS][A_COLUMNS],int B[B_ROWS][B_COLUMNS],int C[A_ROWS][B_COLUMNS]);
int main()
{
    int A[A_ROWS][A_COLUMNS] = {,,
                                ,,
                                ,};
    int B[B_ROWS][B_COLUMNS] = {,,,
                                ,,};
    int C[A_ROWS][B_COLUMNS] = {};
    matrix_multiply(A,B,C);
    for(int i=;i<A_ROWS;i++)
    {
        for(int j=;j<B_COLUMNS;j++)
            cout<<C[i][j]<<" ";
        cout<<endl;
    }
    return ;
}
void matrix_multiply(int A[A_ROWS][A_COLUMNS],int B[B_ROWS][B_COLUMNS],int C[A_ROWS][B_COLUMNS])
{
    if(A_COLUMNS != B_ROWS)
        cout<<"error: incompatible dimensions."<<endl;
    else
    {
        int i,j,k;
        for(i=;i<A_ROWS;i++)
            for(j=;j<B_COLUMNS;j++)
            {
                C[i][j] = ;
                for(k=;k<A_COLUMNS;k++)
                    C[i][j] += A[i][k] * B[k][j]; //将A的每一行的每一列与B的每一列的每一行的乘积求和
            }
    }
}

结果：

2、矩阵链乘问题描述

　　给定n个矩阵构成的一个链<A₁,A₂,A₃,.......A_n>，其中i=1,2,...n，矩阵A的维数为p_i-1p_i，对乘积 A₁A₂...A_n 以一种最小化标量乘法次数的方式进行加全部括号。

　　注意：在矩阵链乘问题中，实际上并没有把矩阵相乘，目的是确定一个具有最小代价的矩阵相乘顺序。找出这样一个结合顺序使得相乘的代价最低。

3、动态规划分析过程

1）最优加全部括号的结构

　　动态规划第一步是寻找一个最优的子结构。假设现在要计算A_iA_i+1....A_j的值，计算A_i...j过程当中肯定会存在某个k值（i<=k<j）将A_i...j分成两部分，使得A_i...j的计算量最小。分成两个子问题A_i...k和A_k+1...j，需要继续递归寻找这两个子问题的最优解。

　　有分析可以到最优子结构为：假设A_iA_i+1....A_j的一个最优加全括号把乘积在A_k和A_k+1之间分开，则A_i..k和A_k+1..j也都是最优加全括号的。

2）一个递归解

　　设m[i,j]为计算机矩阵A_i...j所需的标量乘法运算次数的最小值，对此计算A_1..n的最小代价就是m[1,n]。现在需要来递归定义m[i,j]，分两种情况进行讨论如下：

　　当i==j时：m[i,j] = 0，（此时只包含一个矩阵）

　　当i<j 时：从步骤1中需要寻找一个k（i≤k＜j）值，使得m[i,j] ＝min{m[i,k]+m[k+1,j]+p_i-1p_kp_j} （i≤k＜j）。

3）计算最优代价

　　设矩阵Ai的维数为pi- 1pi，i=1,2.....n。输入序列为：p=<p0，p1,...pn>，length[p] = n+1。使用m[n][n]保存m[i,j]的代价，s[n][n]保存计算m[i,j]时取得最优代价处k的值，最后可以用s中的记录构造一个最优解。 书中给出了计算过程的伪代码，摘录如下：

MAXTRIX_CHAIN_ORDER(p)
  n = length[p]-;
  for i= to n
      do m[i][i] = ;
  for t =  to n  //t is the chain length
       do for i= to n-t+
                     j=i+t-;
                     m[i][j] = MAXLIMIT;
                     for k=i to j-
                            q = m[i][k] + m[k+][i] + qi-1qkqj;
                            if q < m[i][j]
                               then m[i][j] = q;
                                    s[i][j] = k;
  return m and s;

MATRIX_CHAIN_ORDER具有循环嵌套，深度为3层，运行时间为O(n³)。如果采用递归进行实现，则需要指数级时间Ω(2ⁿ)，因为中间有些重复计算。递归是完全按照第二步得到的递归公式进行计算，递归实现如下所示：

int recursive_matrix_chain(int *p,int i,int j,int m[N+][N+],int s[N+][N+])
{
    if(i==j)
       m[i][j] = ;
    else
    {
        int k;
        m[i][j] = MAXVALUE;
        for(k=i;k<j;k++)
        {
            int temp = recursive_matrix_chain(p,i,k,m,s) +recursive_matrix_chain(p,k+,j,m,s) + p[i-]*p[k]*p[j];
            if(temp < m[i][j])
            {
                m[i][j] = temp;
                s[i][j] = k;
            }
        }
    }
    return m[i][j];
}

对递归算计的改进，可以引入备忘录，采用自顶向下的策略，维护一个记录了子问题的表，控制结构像递归算法。完整程序如下所示：

int memoized_matrix_chain(int *p,int m[N+][N+],int s[N+][N+])
{
    int i,j;
    for(i=;i<=N;++i)
        for(j=;j<=N;++j)
        {
           m[i][j] = MAXVALUE;
        }
    return lookup_chain(p,,N,m,s);
}

int lookup_chain(int *p,int i,int j,int m[N+][N+],int s[N+][N+])
{
    if(m[i][j] < MAXVALUE)
        return m[i][j]; //直接返回，相当于查表
    if(i == j)
        m[i][j] = ;
    else
    {
        int k;
        for(k=i;k<j;++k)
        {
            int temp = lookup_chain(p,i,k,m,s)+lookup_chain(p,k+,j,m,s) + p[i-]*p[k]*p[j];  //通过递归的形式计算，只计算一次，第二次查表得到
            if(temp < m[i][j])
            {
                m[i][j] = temp;
                s[i][j] = k;
            }
        }
    }
    return m[i][j];
}

4)构造一个最优解

第三步中已经计算出来最小代价，并保存了相关的记录信息。因此只需对s表格进行递归调用展开既可以得到一个最优解。书中给出了伪代码，摘录如下：

PRINT_OPTIMAL_PARENS(s,i,j)
  if i== j
     then print "Ai"
  else
     print "(";
     PRINT_OPTIMAL_PARENS(s,i,s[i][j]);
     PRINT_OPTIMAL_PARENS(s,s[i][j]+,j);
     print")";

4、编程实现

　　采用C++语言实现这个过程，现有矩阵A₁(30×35)、A₂(35×15)_、A3(15×5)、A4(5×10)、A5(10×20)、A6(20×25)，得到p=<30,35,15,5,10,20,25>。实现过程定义两个二维数组m和s，为了方便计算其第一行和第一列都忽略，行标和列标都是1开始。完整的程序如下所示：

#include <iostream>
using namespace std;

#define N 6
#define MAXVALUE 1000000

void matrix_chain_order(int *p,int len,int m[N+][N+],int s[N+][N+]);
void print_optimal_parents(int s[N+][N+],int i,int j);

int main()
{
    int p[N+] = {,,,,,,};
    int m[N+][N+]={};
    int s[N+][N+]={};
    int i,j;
    matrix_chain_order(p,N+,m,s);
    cout<<"m value is: "<<endl;
    for(i=;i<=N;++i)
    {
        for(j=;j<=N;++j)
            cout<<m[i][j]<<" ";
        cout<<endl;
    }
    cout<<"s value is: "<<endl;
    for(i=;i<=N;++i)
    {
        for(j=;j<=N;++j)
            cout<<s[i][j]<<" ";
        cout<<endl;
    }
    cout<<"The result is:"<<endl;
    print_optimal_parents(s,,N);
    return ;
}

void matrix_chain_order(int *p,int len,int m[N+][N+],int s[N+][N+])
{
    int i,j,k,t;
    for(i=;i<=N;++i)
        m[i][i] = ;
    for(t=;t<=N;t++)  //当前链乘矩阵的长度
    {
        for(i=;i<=N-t+;i++)  //从第一矩阵开始算起，计算长度为t的最少代价
        {
            j=i+t-;//长度为t时候的最后一个元素
            m[i][j] = MAXVALUE;  //初始化为最大代价
            for(k=i;k<=j-;k++)   //寻找最优的k值，使得分成两部分k在i与j-1之间
            {
                int temp = m[i][k]+m[k+][j] + p[i-]*p[k]*p[j];
                if(temp < m[i][j])
                {
                    m[i][j] = temp;   //记录下当前的最小代价
                    s[i][j] = k;      //记录当前的括号位置，即矩阵的编号
                }
            }
        }
    }
}

//s中存放着括号当前的位置
void print_optimal_parents(int s[N+][N+],int i,int j)
{
    if( i == j)
        cout<<"A"<<i;
    else
    {
        cout<<"(";
        print_optimal_parents(s,i,s[i][j]);
        print_optimal_parents(s,s[i][j]+,j);
        cout<<")";
    }

}

结果：

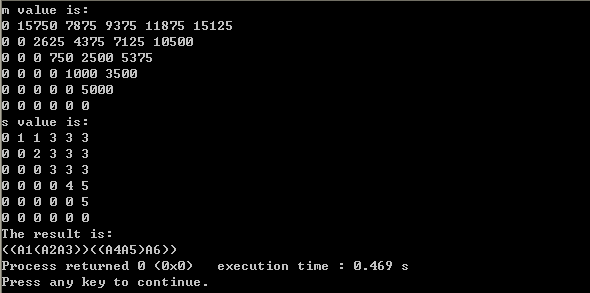
5、总结

　　动态规划解决问题关键是分析过程，难度在于如何发现其子问题的结构及子问题的递归解。这个需要多多思考，不是短时间内能明白。在实现过程中遇到问题就是数组，数组的下标问题是个比较麻烦的事情，如何能够过合理的去处理，需要一定的技巧。