【HDU 2966 k-dimensional Tree 入个门】

·“k-d树是一种分割k维数据空间的数据结构。主要应用于多维空间关键数据的范围搜索和最近邻搜索……”’'

 

·英文题，述大意：
      给出平面内n个点(n<=100000,0<=x,y<=10⁹),我们的任务是按读入顺序输出距离每个点最近的点离它的欧几里得距离的平方。

·分析：

     由于是二维，我们可以先考虑一维的情况。若是一维，那我们只需要轻松地维护序列的有序性然后比较一下该元素的左右两个元素最后得到答案，对于维护，我们可以选用Treap,Sort()等。推广到二维，按照上述思路，我们需要维护两个关键字(x,y)的有序性，那么就需要用到嵌套数据结构。这道题的升级版是K维空间内找到最近点，如果我们依旧这样思考，就只能使用树套树套树套树……了吗？

     引入KD树的优秀思想——关键字按建树层数轮流起作用。在网络上会经常看见这样的图片来描述KD树的建树方式：

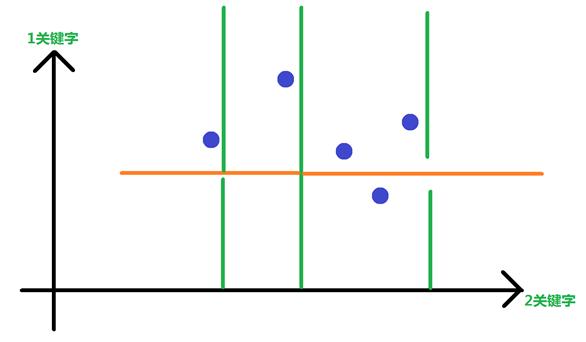
     这是啥？这是对二维情况的描述，是使用两个关键字不断划分区间，实质是划分点。这样做是为何？注意我们的目的，是找到最近点！所以我们要找到和这个点的X,Y坐标尽量接近的点，它才可能成为答案。

     一颗种在花园里的KD树一般会有这两个过程：   

   （一）建树：

    建树的思想就是上文的关键字轮流划分。我们先回忆线段树的建树，只有一个关键字：下标(或者权值)。所以线段树就可以一直通过mid=l+r>>1不断划分，其实就是默认了唯一关键字。那么对于KD树（本题是二维KD树），建树过程和线段树差不多，也采用二分区间的思想，不过，对于每一层我们关键字交替起作用——例如，本层的关键字轮到了X，那么我们就先找到序列按X排序后的中间数（中位数），然后将小于等于X的点全部塞到左儿子，其余的塞到右儿子，依旧像线段树一样对儿子进行递归操作。我们设M为节点的中位数下标，那么对于建好的KD树的任意节点区间，都满足在当前关键字下，在M左边的点的关键字值小于等于M，在M右边的点的关键字大于M。这样为后来的查询操作打下基础。

   （二）查询：

    设现在我们要找到离点A(x1,y1)最近的点的距离的平方。最直接的思路就是我们像线段树一样遍历进行查询，对于每个区间[l,r]的M(中位数的下标)，为了使得“坐标尽量靠近”，我们规定如果A点的当前关键字大于M点的当前关键字，那么就在左儿子中找，与此同时于每个M都算出与A的距离来更新答案。但是这样的思路有一个缺陷，那就是可能存在这样的情况：一个点的X很大，但是Y很小，但由于X的大使得我们决定访问另一边的点，就错过了它，但是它可能就是答案呐！所以在访问一个儿子结束后，我们需要判断一下，

先如个图啦：

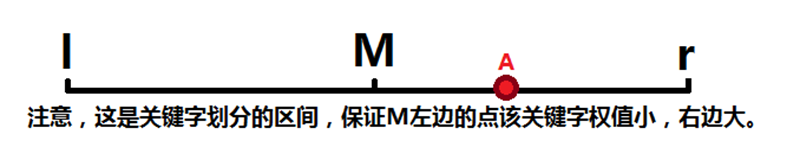
     根据上文，我们发现A的关键字权值大于M，所以要在区间[M+1,r]之间查找，假设找到的最优答案是P，但是如果有：Sqr(AM)<P那么说明可能在[l,M]区间中存在贡献答案的点，因为这个式子相当于是用一个关键字的距离平方来与答案比较，只要另一个关键字小，那么完全可能更新答案。

     代码之中有一些精妙操作。好吧，它来了。

 

 #include<stdio.h>
 #include<algorithm>
 #define ll long long
 #define S(a) ((1LL*a)*(a))
 #define go(i,a,b) for(int i=a;i<=b;i++)
 using namespace std;const int N=;
 struct P{int p[];}a[N],A[N];int T,D,n;ll ans;
 bool cmp(P X,P Y){return X.p[D]<Y.p[D];};
 ll Dis(P X,P Y){return S(X.p[]-Y.p[])+S(X.p[]-Y.p[]);}
 void build(int l,int r,int d)
 {
     if(l>r)return;int M=l+r>>;D=d;
     nth_element(a+l,a+M,a+r+,cmp);
     build(l,M-,d^);build(M+,r,d^);
 }
 void query(int l,int r,int d,P u)
 {
     if(l>r)return;
     int M=l+r>>,L=l,R=M-;ll dis=Dis(a[M],u);
     if(dis&&(ans==||ans>dis))ans=dis;
     if(u.p[d]>a[M].p[d])L=M+,R=r;query(L,R,d^,u);
     if(S(u.p[d]-a[M].p[d])<ans)query(l+M+-L,r+M--R,d^,u);
 }
 int main()
 {
     scanf("%d",&T);while(T--&&scanf("%d",&n))
     {
         go(i,,n)scanf("%d%d",a[i].p,a[i].p+),A[i]=a[i];build(,n,);
         go(i,,n)ans=,query(,n,,A[i]),printf("%lld\n",ans);
     }
 return ;}//Paul_Guderian

                                                      

经过濒临疯狂的彻底孤独，

经过狂乱的空空如也的一无所有，

经过一直凉到脚心底的自暴自弃…… ————汪峰《瓦解》