Day 1 上午

唉，上午就碰到一个开不了机的电脑，白白浪费了半个小时，真的难受QwQ

POINT1 枚举

枚举也称作穷举，指的是从问题所有可能的解的集合中一一枚举各元素。

用题目中给定的检验条件判定哪些是无用的，哪些是有用的。能使命题成立的即为其解。

例一

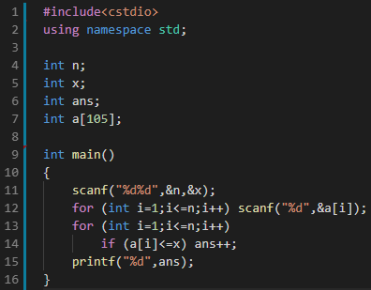
一棵苹果树上有n个苹果，每个苹果长在高度为Ai的地方。

小明的身高为x他想知道他最多能摘到多少苹果

数据范围： 1 ≤ n, Ai, x ≤ 100

题解
问题相当于询问有多少i满足Ai <= x，考虑用for循环枚举每一个苹果是否能被摘到即可 
  

例二
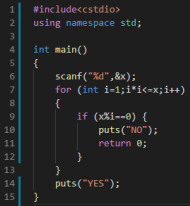
判断一个数X是否是素数
1 ≤ X ≤ 10

考虑定义，若X为合数，则必然有：∃1 < i < X, i|X

我们考虑直接枚举每个i，看他是否为X的因子

时间复杂度O(N)，不符合要求

事实上我们发现，假设X是一个合数，那么必然有:X = a * b,必然有：
min(a, b) <= √X

因此我们枚举的范围可以从X变为√X
时间复杂度O(√N)

例三

求[l, r]这段区间中有多少素数
1 ≤ l ≤ r ≤ 10⁶

一个显然的想法是利用for循环枚举[l, r]中的每一个数。然后利用例二中的知识O(√X)进行判断
整体复杂度O(N√N),不符合要求

筛法求素数
仍然考虑枚举判断每个数是否是素数，但我们这次从2开始判断。
 
考虑对于任意一个数x,不论x是否为素数，都有x*2,x*3,x*4...为合数。我们“筛”掉这些必然为合数的
数。
 
那么当我们枚举到i，i还没有被筛掉，那么i必然为素数。
时间复杂度O(NlogN)
在判断是质数的同时计数即可

例四

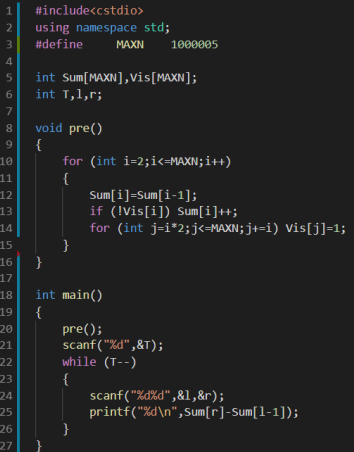
T次询问，每次询问[l, r]中有多少素数
1 ≤ T ≤ 10⁵, 1 ≤ l ≤ r ≤ 10⁶

我们用ANSL,R来表示[l, r]中有多少素数，发现ANSL,R = ANS1,R - ANS1,L-1
于是我们可以维护一个素数个数的前缀和Sum[i]表示[1, i]中
有多少素数
每次询问就输出Sum[r] - Sum[l - 1]即可

已知n个整数x1, x2, .., xn,以及一个整数k,k < n。从n个数字中任选k 个整数相加，可分别得到一系列的和。

例如当n = 4, k = 3,四个整数分别为3,7,12,19时，可得全部的组合与他们的和为:

3 + 7 + 12 = 22
3 + 7 + 19 = 29
7 + 12 + 19 = 38
3 + 12 + 19 = 34
现在，要求计算出和为素数的组合共有多少种。
例如上例，只有一种组合的和为素数：3 + 7 + 19 = 29
1 ≤ n ≤ 20, k < n
1 ≤ x1, x2, .., xn ≤ 5 * 10⁶

首先我们来考虑如何枚举这样的组合。
我们用ai来表示第i个数是否被选
ai = 1表示这个数被选择了
ai = 0表示这个数未被选择
枚举过程相当于枚举了一组二进制状态
比如对于五个数1,2,3,4,5
01010表示我们选择了2,4,未选择1,3,5

在不考虑k的限制的情况下，我们枚举所有组合就相当于枚举00..00(n个0) → 11..11(n个1)
对于任意一种中间状态，0的个数+1的个数为n
我们假设这是一个长为n的二进制数，我们将它转换成十进制。
事实上就是枚举了一个数，范围是[0, 2n)
判断位置i是否为1使用位运算来完成

例六
求[l,r]中有多少数既是回文数又是素数
1 ≤ l ≤ r ≤ 107

策略一
枚举每个数，判断他是不是回文数，判断他是不是素数
时间复杂度O(N√N + NlogN)

策略二
预处理出区间所有素数，枚举素数判定是否是回文数
时间复杂度O(NlogN)

策略三
枚举区间内所有回文数，判断是否是素数
枚举回文数即枚举一个数的前一半，再手动扩展成完整的数
另外，偶数位数的回文数都必然是11的倍数，不需要枚举。
时间复杂度O(√N * √N) = O(N)

枚举的优点
简单明了，分析直观
能够帮助我们更好地理解问题
运用良好的枚举技巧可以使问题变得更简单

缺点
时空间效率低
往往没有利用题目中的特殊性质
产生了大量冗余状态

POINT2 搜索

本质上是一种枚举
搜索算法一般做一些普通的枚举不方便表达状态的情况

例题
给出一个N*N的迷宫，求从起点出发，不经过障碍物到达终点的最短距离

解决这类问题一般有两种方式
1.深度优先搜索（dfs）
2.广度优先搜索 （bfs）

前置知识
栈：后进先出的数据结构
支持的操作：
加入一个数
删除最晚加入的数
查询最晚加入的数
实现：一个数组+一个用于指向栈顶位置的变量

系统内部递归即使用了栈
例如求斐波那契数列的第n项

DFS的操作过程

遇到岔路口，随便选一个走

走不到终点就换条路

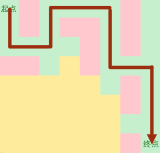
当然也可以这么走

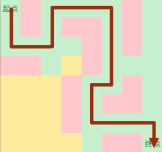
DFS的优缺点
优点：占用空间小（只需要记录从起点到当前点的路径）
代码短
缺点：获得的不一定是最优解
在图上路径非常多的时候，复杂度可能会达到指数级别

前置知识
队列：先进先出的数据结构
支持的操作：
加入一个数
删除最早加入的数
查询最早加入的数
实现：一个数组+头下标+尾下标

BFS的操作过程

开始走

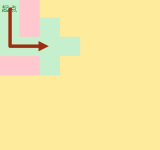
走到岔路口，都要走

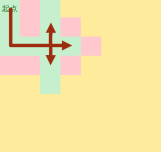
标记步数

疯狂操作

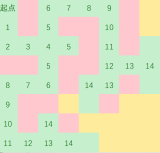
最终

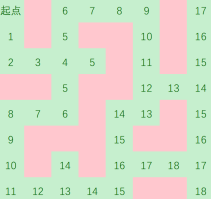
要注意这里每一个步数相同的点都是同时向外走的，所以不会出现两个路径矛盾的情况

BFS的优缺点
优点：找到答案时找到的一定是最优解
复杂度不会超过图的大小
缺点：需要维护一个“当前箭头的集合”，空间较大

DFS和BFS的区别
DFS:能走就走，走不了才回头
BFS:我全都要

应用:图的遍历
G = (V , E)被称为一张图,则其包含两部分:
1.点集|V | = n,即有n个点,标号分别为1, 2, ..., n
2.边集|E| = m,有m条边(ui, vi),表示第ui个点和第vi个点有一条边相连.
边有向边和无向边之分,(u, v)是无向边,则u能直接走到v,v能直接走到u.

图的存储结构
1.画图
2.邻接矩阵存储,用A[x][y] = 0/1表示.优点是便于加删,但是需要O(N2)的空间.
3.直接用vector存下所有的边(邻接表法).优点是空间和访问比较快,缺点是删除比较麻烦.

图的连通块
在本课中我们基本只考虑无向图.
若a沿着边走可以到b,则称a与b在同一个连通块中,称a与b连通.
显然a与b连通,b与c连通,则a与c肯定连通.
一张图可以被分成若干个两两连通的块.

图的遍历
给出一张n个点m条边的图,分别求出每个连通块.
n, m ≤ 100000.
用bfs还是dfs?

每次任选一个没有被访问过的点,然后从这个点开始bfs,找到所有和它连通的点.
时间复杂度O(N + M)(用什么方式可以让每条边被遍历常数遍?).

树

若一张图只有恰好n - 1条边,并且任意两个点之间都是连通的,则称这张图是一棵树.
树的性质:任意两点之间有且只有一条路可以相互到达.
有根树:随便给出一个点x,设x是根,然后从x开始遍历,假设你从a一步遍历到了b,则记fab = a,容易发现每个点的父亲都是
唯一的.x的父亲记为0.

给出一棵n个点的树,将它转化为有根树的形式(假定以1为根)?
N ≤ 100000
用bfs还是dfs?

理论上来说bfs和dfs都可以,但一般我们用dfs构造.
复杂度O(N).

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<set>
#include<vector>
#include<map>
#include<queue>

#define N 1000005
#define M 20000005

#define ls tree[t].l
#define rs tree[t].r
#define Ls tree[t1].l
#define Rs tree[t1].r
#define mid ((l+r)>>1)

#define mk make_pair
#define pb push_back
#define fi first
#define se second

using namespace std;

vector<int>v[N];

int i,j,m,n,p,k,size[N],fa[N];

void dfs(int x)
{
        int i;
        size[x]=;
        for (i=;i<(int)v[x].size();++i) //遍历每条边
        {
                int p=v[x][i];
                if (fa[x]==p) continue; //如果这条边连向它的父亲，就不用管了
                fa[p]=x; //否则是它的儿子,更新fa数组,然后dfs下去算
                dfs(p);
                size[x]+=size[p]; //可以顺便计算出它向下一共有多少点
        }
}

int main()
{
        scanf("%d",&n);
        for (i=;i<n;++i) //把所有的边加进每个点的vector当中
        {
                int x,y;
                scanf("%d%d",&x,&y);
                v[x].push_back(y);
                v[y].push_back(x);
        }
        dfs();
}

例一
要求输出1 ∼ n构成的全排列

题解
用一个Vis数组记录每个数字是否被用过
DFS的经典应用

例二
八数码游戏是一种非常无聊的游戏。给定一个3*3的格子，在其中8个格子中放置整数1 ∼ 8，剩下一个格子空着（用0表示）。
每次操作时，你可以选择将某个与空格相邻的数字移动到空格上。给定一个初始局面，求最少需要多少次操作才能将局面变成

1 2 3
4 5 6
7 8 0

题解

状态？0 ∼ 8 的一个排列
转移？一步能够到达的其他排列
BFS or DFS? BFS

多组数据怎么做？

题解

考虑倒着进行游戏过程。
所有状态都是由最终状态转移得到的
因此我们以最终态为起点做一遍BFS即可预处理出所有状态
的答案

例三
给出一个大小为N*M的迷宫，问从起点到终点最少经过多
少障碍物
1 ≤ n, m ≤ 1000

题解
维护两个队列，分别表示当前答案和答案+1的点
每次先走同层的点即可

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<ctime>
#include<cmath>
#include<map>
#include<set>
#include<bitset>
#include<vector>

#define ls (t<<1)
#define rs ((t<<1)|1)

#define N 1005
#define M 200005
#define K 17

#define pb push_back
#define fi first
#define se second
#define mk make_pair

using namespace std;

int i,j,m,n,p,k,r[];

int vis[N][N];

pair<int,int> Q[][N*N];

char c[N][N];

const int X[]={-,,,};
const int Y[]={,,-,};

int check(int x,int y)
{
        if (x<=||y<=||x>n||y>m) return ;
        if (vis[x][y]) return ;
        return ;
}

void bfs(int x,int y)
{
        int i,l,now=;
        Q[][r[]=]=make_pair(x,y);
        memset(vis,-,sizeof(vis));
        vis[x][y]=;
        for (;;)
        {
            now^=;
            if (!r[now]) return;
            for (l=;l<=r[now];++l)
            {
                    int ax=Q[now][r[now]].first,ay=Q[now][r[now]].second;
                    for (i=;i<;++i)
                        if (check(ax+X[i],ay+Y[i]))
                    {
                            int ck=c[ax+X[i]][ay+Y[i]]=='#';
                            if (!ck)
                            {
                                    vis[ax+X[i]][ay+Y[i]]=vis[ax][ay];
                                    Q[now][++r[now]]=make_pair(ax+X[i],ay+Y[i]);
                            }
                            else
                            {
                                    vis[ax+X[i]][ay+Y[i]]=vis[ax][ay]+;
                                    Q[now^][++r[now^]]=make_pair(ax+X[i],ay+Y[i]);
                            }
                    }
            }
        }
}

int main()
{
    scanf("%d%d",&n,&m);
    for (i=;i<=n;++i) scanf("%s",c[i]+);
    for (i=;i<=n;++i)
        for (j=;j<=m;++j)
            if (c[i][j]=='S') bfs(i,j);
    for (i=;i<=n;++i)
        for (j=;j<=m;++j)
            if (c[i][j]=='E') printf("%d\n",vis[i][j]);
}

跳房子
跳房子是大家小时候的体育游戏之一，游戏的规则简单易懂、具有可变性。

我们在地面上画出一个个房子，然后扔石子，根据石子的落地位置确定跳到哪个房子。

我们将房子抽象为x轴上的连续的正整数坐标点，第i个房子的坐标为i，并假设房子个数无限。

我们的游戏规则如下：
1. 石子落到房子内，记为H，我们可以跳到当前坐标的3倍坐标位置。

2. 石子落到房子外，记为O，我们需跳回当前坐标折半并向下取整的坐标位置。 
例如，初始在第1个房子，要想到达第6个房子，既可以HHHOO，也可以HHOHO。
请你编一个程序，给出从第n个房子到第m个房子所需要的最少跳跃次数k和石子的扔法。若最少跳跃次数下存在多种扔法，则选取字典序最小的扔法。
1 ≤ N, M ≤ 1000,数据保证在25步之内有解。

题解

这个题使用BFS可能会有些问题，因为无法预知最远能跳到多远。

但是注意到数据在25步之内一定会出解，我们不妨考虑暴力dfs,在dfs的时候遵循先H后O的规律.

时间复杂度O(2²⁵).

推箱子
推箱子是一个很经典的游戏.今天我们来玩一个简单版本.在一个M * N的房间里有一个箱子和一个搬运工,搬运工的工作

就是把箱子推到指定的位置,注意,搬运工只能推箱子而不能拉箱子,因此如果箱子被推到一个角上那么箱子就不能再被

移动了,如果箱子被推到一面墙上,那么箱子只能沿着墙移动.现在给定房间的结构,箱子的位置,搬运工的位置和箱子要被推去的位置,请你计算出搬运工至少要推动箱子多少格.

N, M ≤ 7

题解：

简单的BFS,我们暴力记录人的位置和箱子的位置作为一个4维的状态，然后进行bfs.

时间复杂度O(N * M * N * M)

迷宫入口
爱好探险的你，找到一座装满了宝藏的迷宫的入口，你看到入口的大门上有一个边长为s的正方形的大锁，旁边散落

着n块正方形的金属小片，你意识到锁的钥匙，即是用这n小块，拼成大门上的正方形，你想知道是否能拼成这把钥匙打开迷宫的大门。

n ≤ 16, 1 ≤ ci ≤ 10.

题解

我们从低到高，从左往右的一个个放入正方形。也就是说我们维护下表面的轮廓。
每次，我们选择一个最低的点放正方形，如果有多个就选择一个最靠左的。
加入一个正方形时，需要判断这一整段是否都是平的，然后就放上去继续递归.
一个非常强力的剪枝是ci ≤ 10但n = 16,那么每次我们不要去重复的选择一个长度相同的正方形，这样就能通过本题了.

时间复杂度O(玄学).

华容道
如下图所示，共有三个连通的由1*1单位正方形构成的不规则固体块。

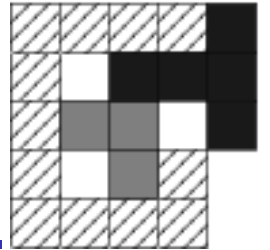
每次操作可以将任一个固体块向上、向下、向左或向右平移一格，但是在平移的过程中不能使得任何两个固体块有重合的部分。问是否能够通过上述的操作使得三个固体块完全分离。完全分离指对于任何两个不同的固体块，完全覆盖它们的最小的长方形没有重合的部分。如果能做到，输出所需要的最小的步数，如果做不到，输出-1。

所有方块的坐标范围都在0到9之间。

题解：

是一个相当复杂的BFS最短路题,难点在于如何构建合适的
状态.

因为每一个方块的坐标范围都是0~9，所以将坐标区间设置在-20~20之间可以保证三个联通块分开

我们可以设计初始状态(x1, y1, x2, y2, x3, y3)，分别记录三个块的左上角位置，注意到每一维的坐标可能在(-20, 20)之间，所以状态会很多.

我们来尝试将一些状态隐藏起来，不妨强制x1, y1是当前坐标轴的(0,0),然后这样我们只需要记录另外两个点的位置就行了。因为事实上只有相对位置是有用的，可以少计一个。

注意到每一维的范围仍然是(-20, 20),所以状态数被我们缩减到了40⁴就可以接受了.

时间复杂度O(40⁴)

这里要注意这是用一个点的移动来代替联通块的移动，但是判断的时候还是要整个联通块判断

汇♂合
给出一张n × m的网格图，其间有障碍、空地、A的基地、B的基地以及C的基地。

现在A, B, C都随机选一个自己的基地作为起点，接着走到一个到三个点距离和最小的点汇合。

求汇♂合的距离和期望。
n, m ≤ 150，A的基地数，B的基地数 ≤ 50。

题解：

因为A, B的基地数很少，所以枚举A, B的起点x, y。
将图上所有点的初始距离，定义为它们到点x和点y的距离和。

做一遍“多源多汇”的最短路，以求出每个C基地的答案。
用BFS实现最短路，效率为O(|A||B|nm)。

在做这类题的时候，我们要考虑

深搜什么策略

宽搜什么状态

记忆化搜索：

来看最初的斐波那契数列

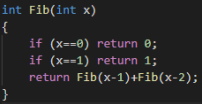
时间复杂度？
O(2N)

发现复杂度的主要来源是有很多次重复计算考虑用f[i]记录Fib数列的第i项当搜索到这一项时不再进行递归，而是直接返回答案 记忆化之后搜索的复杂度一般也很容易确定，与需要记录的状态数有关