【2016北京集训测试赛（十）】 Azelso （期望DP）

Time Limit: 1000 ms   Memory Limit: 256 MB

Description

---

题解

状态表示：

　　这题的状态表示有点难想......

　　设$f_i$表示第$i$个事件经过之后，到达终点之前，不再回到事件$i$或事件$i$的左边的概率，反过来说就是可以在右边乱绕，若事件$i$的位置为pos，“右边”指的就是$(pos,h]$。

　　我们将第$i$个事件到第$i+1$个事件中间这一段路程记为$S_i$，那么期望经过$S_i$的次数就为$1/f_i$。

　　为什么是$1/f_i$呢？具体来说，只在右边乱绕，最左也只能到达$i+1$；一旦跨越到i或i的左边位置，那么S就必须要被经过了。所以$f_i$越小，被踢到左边或起点的概率就越大，经过$S_i$的概率和期望也就越大。

Orzhy Orzyww Orzyxq

状态转移：

　　我们来反向转移嘿。

　　考虑$f_i$，我们应该从$f_i+1$得到。

　　我们令$p_i$为第$i$个事件的成功概率（获得Flag或打败敌人的概率）。

• 　　如果$i+1$个事件是一个敌人，那么

　　　　　　$f_i=f_{i+1}*p_{i+1}$

• 　　如果$i+1$个事件是一面FLAG，那么

　　　　　　$f_i=f_{i+1}+(1-f_{i+1})*p_{i+1}*f_{i+1}+((1-f_{i+1})*p_{i+1})^2*f_{i+1}+...+((1-f_{i+1})*p_{i+1})^k*f_{i+1}$

　　　　　　　  $=f_{i+1}*(1+p_{i+1}*(1-f_{i+1})+p_{i+1}^2*(1-f_{i+1})^2+...+p_{i+1}^k*(1-f_{i+1})^k)$

　　　　　　${k\to\infty}$

　　　　   可以运用极限等式的求法可以将极限部分转换为下式的分母：

　　　　　    $f_i=\frac{f_{i+1}}{(1-p_{i+1}*(1-f_{i+1}))}$

　　    这是什么意思呢？

　　　　　看回第一个式子，$(1-f_{i+1})$的意思是被弹回i+1或i+1的左边，$p_{i+1}$的意思是被$i+1$这个旗子留住，$f_{i+1}$的意思是从$i+1$一路走到终点的概率。

　　　　　$(1-f_{i+1})*p_{i+1}*f_{i+1}$意思是按下图的1-2-3顺序执行

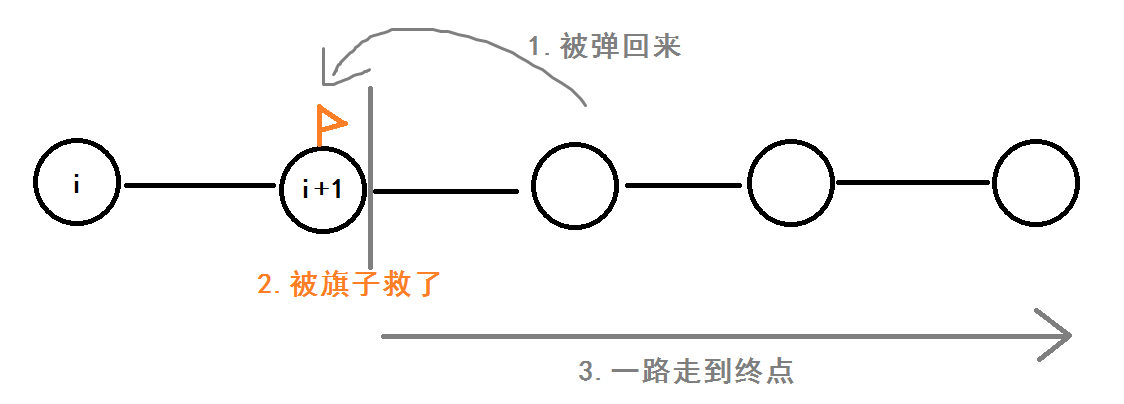
　　　　　同理，$((1-f_{i+1})*p_{i+1})^2*f_{i+1}$表示1-2-1-2-3，$((1-f_{i+1})*p_{i+1})^3*f_{i+1}$表示1-2-1-2-1-2-3，以此类推即可。

　　　　　计算时所有除法转为逆元，记得%多一点（记8.17）