从"汉诺塔"经典递归到JS递归函数

前言

参考《JavaScript语言精粹》

递归是一种强大的编程技术，他把一个问题分解为一组相似的子问题，每一问题都用一个寻常解去解决。递归函数就是会直接或者间接调用自身的一种函数，一般来说，一个递归函数调用自身去解决它的子问题。

"汉诺塔"经典递归问题

"汉诺塔"是印度的一个古老传说，也是程序设计中的经典的递归问题，是一个著名的益智游戏：

　　题目如下：

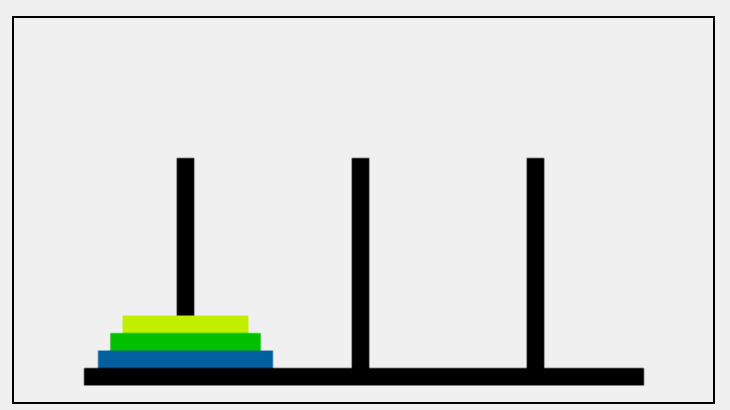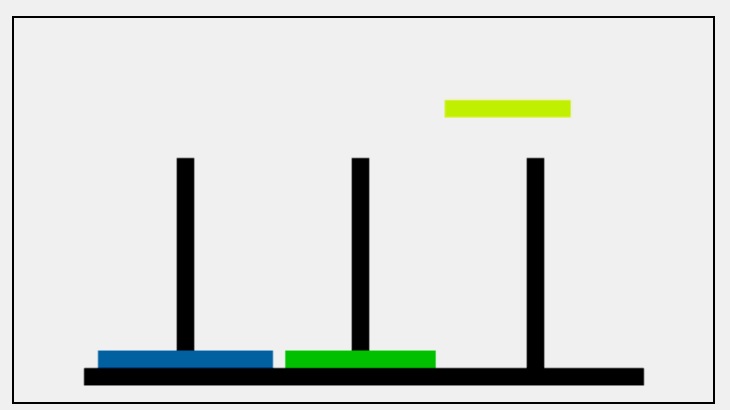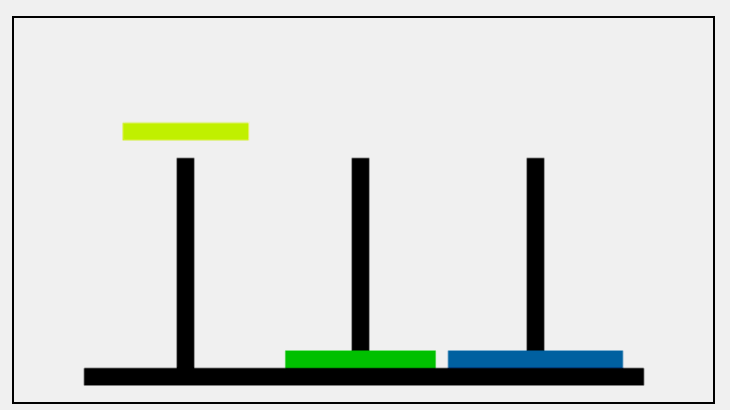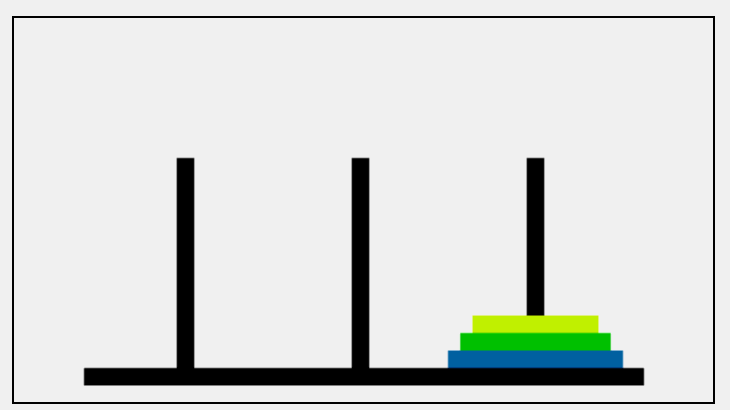
　　　　塔上有三根柱子和一套直径各不相同的空心圆盘，开始时源柱子上的所有圆盘都按从大到小的顺序排列。目标是通过每一次移动一个圆盘到另一根柱子上，最终把一堆圆盘移动到目标柱子上，过程中不允许把较大的圆盘放置在较小的圆盘上；

　　　　

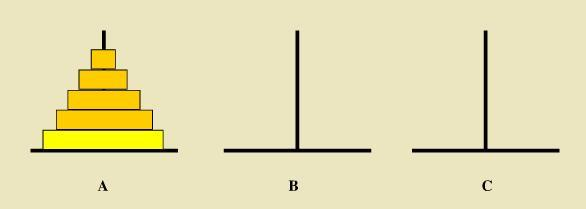
寻找规律（把所有的圆盘移动到C）：

　　1）n(圆盘个数) == 1

　　　　第一次：1号盘  A -> C      sum(移动次数) = 1

　　2）n == 2

　　　　第一次：1号盘 A -> B

　　　　第二次：2号盘 A -> C

　　　　第三次：1号盘 B -> C　　sum = 3

　　3）n == 3

　　　　第一次：1号盘 A -> C

　　　　第二次：2号盘 A -> B

　　　　第三次：1号盘 C -> B

　　　　第四次：3号盘 A -> C

　　　　第五次：1号盘 B -> A

　　　　第六次：2号盘 B -> C

　　　　第七次：1号盘 A -> C　　sum = 7

　　　

　　故不难发现规律,移动次数为：sum = 2^n - 1　

算法分析（递归）：

　　把一堆圆盘从一个柱子移动另一根柱子，必要时使用辅助的柱子。可以把它分为三个子问题：

　　　　首先，移动一对圆盘中较小的圆盘到辅助柱子上，从而露出下面较大的圆盘，

　　　　其次，移动下面的圆盘到目标柱子上

　　　　最后，将刚才较小的圆盘从辅助柱子上在移动到目标柱子上

　　 把三个步骤转化为简单数学问题：

　　　　（1）     把 n-1个盘子由A 移到 B；

　　　　（2）     把 第 n个盘子由 A移到 C；

　　　　（3）     把n-1个盘子由B 移到 C；

　　我们创建一个JS函数，当它调用自身的时候，它去处理当前正在处理圆盘之上的圆盘。最后它回一个不存在圆盘去调用，在这种情况下，它不在执行任何操作。

JavaScript源代码实现

var hanoi = function(disc,src,aux,dst){

    if(disc>0){

        hanoi(disc-1,src,dst,aux);

        console.log(' 移动 '+ disc +  ' 号圆盘 ' + ' 从 ' + src +  ' 移动到 ' +  dst);

        hanoi(disc-1,aux,src,dst)

    }

}

hanoi(3,'A','B','C')

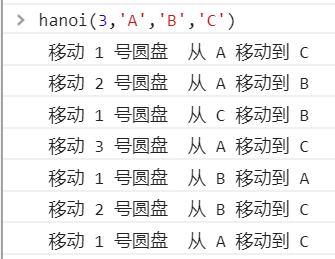
整个算法的思路是：

1. 将A柱子上的n-1个盘子暂时移到B柱子上
2. A柱子只剩下最大的盘子，把它移到目标柱子C上
3. 最后再将B柱子上的n-1

JS递归函数遍历Dom

　　递归函数可以非常高效的操作D树形结构，在JavaScript有一种"天然的树形结构"浏览器端的文档对象模型（Dom）。每次递归调用时处理指定树的一小段。

/*      我们定义一个walk_the_DOM函数，
  1） 它从某个指定的节点开始，按指定HTML源码的顺序，访问树的每个节点
   2）它会调用一个函数，并依次传递每个节点给它，walk_the_DOM调用自身去处理每一个节点
*/
var walk_the_DOM = function walk( node , func ) {

    func(node);

    node = node.firstChild;

    while (node) {

        walk( node , func );

        node = node.nextSibling;

     }    

}

/*    在定义一个getElementByAttribute函数
1） 它以一个属性名称字符串和一个可选的匹配值作为参数
2） 它调用walk_the_DOM，传递一个用来查找节点属性名的函数作为参数，匹配得节点都会累加到一个数组中
*/
              var getElementsByAttribute=function(att,value){
                var results=[];

                walk_the_DOM(document.body,function(node){

                    var actual=node.nodeType===1&&node.getAttribute(att);

                    if(typeof actual==='string' &&( actual===value|| typeof value!=='string')){

                        results.push(node);

                    }
                });
                return results;
            }

命名函数表达式和递归

递归问题

求阶乘的函数：

function factorial(num){
    if(num<=1){
        return 1;
    }else{
        return num*factorial(num-1);
    }
}

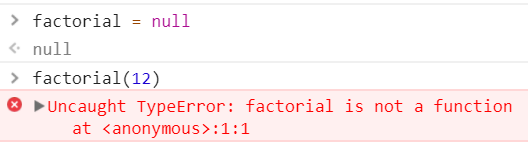
通过将函数factorial设置为null，使原始函数的引用只剩一个, 此时factorial已不再是函数

arguments.callee实现递归

arguments.callee是一个指向正在执行的函数的指针，因此可以用它来实现对函数的递归调用

function factorial(num){
    if(num<=1){
        return 1;
    }else{
        return num*arguments.callee(num-1);
    }
}
var anotherFactorial=factorial;
factorial=null;
anotherFactorial(3) 

用arguments.callee代替函数名，可以确保无论怎样调用函数都不会出问题。因此，在编写递归函数时，使用arguments.callee总比使用函数名更保险。

但是在严格模式下，不能通过脚本访问arguments.callee，访问这个属性会报错

命名函数表达式实现递归

创建一个名为f()的命名函数表达式，然后赋值给factorial，即使把函数赋值给了另一个变量，函数的名字f仍然有效，所以递归调用照样能正常完成。

这种方式在严格模式和非严格模式都可行。

var factorial =function f(num){
    'use strict'
    if(num<=1){
        return 1;
    }else{
        return num* f (num-1);
    }
}

factorial(3
var anotherFactorial=factorial;
factorial=null;
anotherFactorial(3