OI数据结构&&分治 简单学习笔记

持续更新！！！

---

【例题】简单题（K-D tree）

题目链接

线段树

【例题】（环上最大连续和） 给定一个长度为n的环形序列A，其中A1与A_n是相临的，现在有q次修改操作，每次操作会更改其中一个数，请对于每次修改输出修改后的最大连续和。

题目链接：POJ2750

【例题】给定一个长度为n的序列，可以修改任意个数字使其变成原来的相反数，求最小的逆序对数。

左偏树

【例题】派遣 题目链接

左偏树是一种具有左偏性质的堆有序二叉树（这里要注意，堆有序二叉树和二叉堆并不是同一种东西，因此左偏树并不是堆）。每一个节点存储的信息包括左右子节点、关键值以及距离（当然也有很多时候我们需要维护父节点）。

节点的距离可以这样定义：

某个节点被称为外节点，仅当这个节点的左子树或右子树为空。某一个节点的距离即该节点到与其最近的外节点经过的边数。易得，外节点的距离为0，空节点距离为−1。特别的，我们把根结点的距离称为这棵左偏树的距离。

这里有一张来自HolseLee dalao的图，以时空复杂度的角度来分析为什么左偏树是最常见的可并堆：



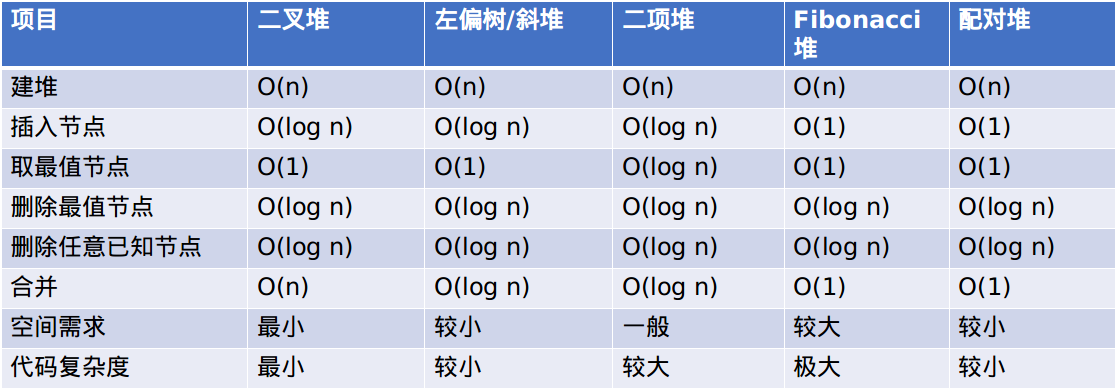
（imone dalao说，斜堆好写啊！）

至于时间复杂度为什么是这样的证明？？没有的我不太会，此处挖坑待补吧。

三维偏序

【例题】给定三个长度为n的排列A,B,C，统计有多少对(i,j)满足\(A_i<A_j,B_i<B_j,C_i<C_j\)。其中\(n<=5e6\)。

解法：

我们先拆成二维偏序的问题。

设x为满足\(A_i<A_j,B_i<B_j\)的个数

y为满足\(B_i<B_j,C_i<C_j\)的个数

z为满足\(C_i<C_j,A_i<A_j\)的个数

显然会有结论：如果满足x,y,z这三种约束条件之二，就能满足题目中所要求的约束条件，我们称之为合法解。在计算这三个二维的时候，同一个合法解会被计算三次。

而不合法解只能被计算一次（因为如果有两次，根据上述所说，它就是合法解了）

我们设这个合法解的数量为c，那么根据排列组合原理，不合法解的数量为\(C_n^2-c\)。

所以我们有\(x+y+z=3c+C_n^2-c\)

所以\(c=\frac{1}{2}(x+y+z+C_n^2)\)

点分治

边分治

如果被菊花图卡了怎么办？加虚点。（只要保证和原图等价即可——点与点之间的边数和原先的一样）

你不知道怎么加虚点？上网搜啊。

【例题】BZOJ2870

？？？？边分治到底是个什么啊？有用吗？有用吗？

链分治

整体二分

使用整体二分的题需要满足以下性质：

• 询问的答案具有可二分性
• 修改对询问的贡献是独立的，相互之间并不影响
• 不同的修改的贡献可以叠加
• 必须离线
  
  顾名思义，就是对所有的询问一起二分。通常而言，这类题的询问是似乎于第几次修改之后满足条件。

莫队

推荐博客：胡小兔良心莫队教程

适用范围：

如果知道区间[l,r]的答案可以快速算出[l,r+1],[l,r-1],[l+1,r],[l-1,r]的答案的题目。

先将序列分成\(\sqrt n\)分块，然后将所有询问做双关键字排序，第一关键字为询问的左端点所在的块，第二关键字为询问的右端点。那么两个询问[l1,r1],[l2,r2]之间转移的时间为(|l1-l2|+(r1-r2|)*t，其中t为转移一次的复杂度。

证明：

对于左端点，在同一块内的转移，一次不超过\(\sqrt n\)，在不同块之间的转移不超过\(\sqrt n\)次。

右端点类似。总共的转移次数为\(O(n\sqrt n)\)级别的。

---

模板专用分割线

• 支持加减乘操作的线段树

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define MAXN 100010
using namespace std;
int n,m,mod;
int a[MAXN];
struct Node{int l,r,add,mul,sum;}t[MAXN<<2];
inline int ls(int x){return x<<1;}
inline int rs(int x){return x<<1|1;}
inline void push_up(int x){t[x].sum=(t[ls(x)].sum+t[rs(x)].sum)%mod;}
inline void f_mul(int x,int mul,int add)
{
	int l=t[x].l,r=t[x].r;
	t[x].sum=(1ll*t[x].sum*mul%mod+1ll*(r-l+1)*add%mod)%mod;
	t[x].mul=(1ll*t[x].mul*mul)%mod;
	t[x].add=(1ll*t[x].add*mul%mod+add)%mod;
}
inline void push_down(int x)
{
	if(t[x].mul!=1||t[x].add)
	{
		f_mul(ls(x),t[x].mul,t[x].add);
		f_mul(rs(x),t[x].mul,t[x].add);
		t[x].mul=1;
		t[x].add=0;
	}
}
inline void build(int x,int l,int r)
{
	t[x].l=l,t[x].r=r;
	t[x].add=0,t[x].mul=1;
	if(l==r) {t[x].sum=a[l]%mod;return;}
	int mid=(l+r)>>1;
	build(ls(x),l,mid);
	build(rs(x),mid+1,r);
	push_up(x);
}
inline void update_add(int x,int ll,int rr,int k)
{
	int l=t[x].l,r=t[x].r;
	if(ll<=l&&r<=rr)
	{
		t[x].sum=(t[x].sum+k*(r-l+1))%mod;
		t[x].add=(t[x].add+k)%mod;
		return;
	}
	push_down(x);
	int mid=(l+r)>>1;
	if(ll<=mid) update_add(ls(x),ll,rr,k);
	if(mid<rr) update_add(rs(x),ll,rr,k);
	push_up(x);
}
inline void update_mul(int x,int ll,int rr,int k)
{
	int l=t[x].l,r=t[x].r;
	if(ll<=l&&r<=rr)
	{
		t[x].sum=(1ll*t[x].sum*k)%mod;
		t[x].mul=(1ll*t[x].mul*k)%mod;
		t[x].add=(1ll*t[x].add*k)%mod;
		return;
	}
	push_down(x);
	int mid=(l+r)>>1;
	if(ll<=mid) update_mul(ls(x),ll,rr,k);
	if(mid<rr) update_mul(rs(x),ll,rr,k);
	push_up(x);
}
inline int query(int x,int ll,int rr)
{
	int l=t[x].l,r=t[x].r;
	if(ll<=l&&r<=rr) return t[x].sum%mod;
	push_down(x);
	int mid=(l+r)>>1;
	int cur_ans=0;
	if(ll<=mid) cur_ans=(cur_ans+query(ls(x),ll,rr));
	if(mid<rr) cur_ans=(cur_ans+query(rs(x),ll,rr));
	return cur_ans%mod;
}
int main()
{
	#ifndef ONLINE_JUDGE
	freopen("ce.in","r",stdin);
	#endif
	scanf("%d%d%d",&n,&m,&mod);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	build(1,1,n);
	for(int i=1;i<=m;i++)
	{
		int op,x,y,k;
		scanf("%d",&op);
		if(op==1)
		{
			scanf("%d%d%d",&x,&y,&k);
			update_mul(1,x,y,k);
		}
		else if(op==2)
		{
			scanf("%d%d%d",&x,&y,&k);
			update_add(1,x,y,k);
		}
		else
		{
			scanf("%d%d",&x,&y);
			printf("%d\n",query(1,x,y));
		}
	}
	return 0;
}