hdu 1025:Constructing Roads In JGShining's Kingdom（DP + 二分优化）

Constructing Roads In JGShining's Kingdom

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 13646    Accepted Submission(s): 3879

Problem Description

JGShining's kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.

Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource. You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource.

With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.

Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.

The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones.

But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.

For example, the roads in Figure I are forbidden.

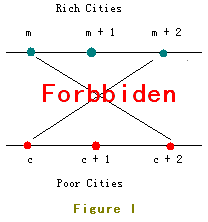
In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^

 

Input

Each test case will begin with a line containing an integer n(1 ≤ n ≤ 500,000). Then n lines follow. Each line contains two integers p and r which represents that Poor City p needs to import resources from Rich City r. Process to the end of file.

 

Output

For each test case, output the result in the form of sample. 
You should tell JGShining what's the maximal number of road(s) can be built. 

 

Sample Input

2
1 2
2 1
3
1 2
2 3
3 1

 

Sample Output

Case 1:
My king, at most 1 road can be built.

Case 2:
My king, at most 2 roads can be built.

Hint

Huge input, scanf is recommended.

 

Author

JGShining（极光炫影）

 

Recommend

We have carefully selected several similar problems for you:  1024 1081 1074 1078 1080 

---

　　

　　动态规划（DP）中的最长上升子序列（LIS）问题，这道题要用二分法解。

　　可以说是 DP+二分 问题。

　　LIS有两种解法，这两种解法的时间复杂度分别为 n^2 , nlogn，分别用朴素查找和二分查找实现。很显然，第二种方法复杂度低，效率高。而这道题正是用到了第二种方法。如果不用二分法，第一种方法提交会超时。

　　链接：LIS 算法解析

 

第一种方法，n^2，朴素查找：

1) 

for i=1 to total-1
　　for j=i+1 to total
　　　　if a[i]<a[j] then
　　　　　　if dp[i]+1 > dp[j]
　　　　　　　　dp[j] = dp[i]+1;

链接：Dynamic Programming之Longest Increasing Subsequence (LIS)问题

2) dp[i]=max{dp[j]}+1;(1<=j<i且a[j]<a[i])

for i=2 to total
　　int m=0;
　　for j=1 to i-1
　　　　if dp[j] > m && a[j] < a[i] then
　　　　　　m=dp[j];
　　dp[i]=m+1;

链接：最长上升子序列LIS算法实现

 

第二种方法，nlogn，二分查找：

　　百度百科 - 二分查找 

　　看了很多博客描述二分查找，还是觉得百度百科上说的最好，几句就把我讲明白了。完全按照百科上的思路实现了一下，提交却WA，虽然我承认我的代码没有网上的写的精炼，但是我没发现逻辑有错误，在这里贴出代码，希望有朋友能帮忙看看问题出在哪里　

 #include <iostream>
 #include <stdio.h>
 using namespace std;
 int a[];
 int q[];
 int BinSearch(int max,int min,int des)    //二分查找第一个比des大的数，并返回坐标
 {
     int l = min,r = max;
     int mid,t;
     while(l<=r){
         mid = (l+r)/;
         if(des<=q[mid]){
             t=mid;
             r=mid-;
         }
         else{
             l=mid+;
         }
     }
     return t;
 }
 int main()
 {
     int n,num=;
     while(cin>>n){
         for(int i=;i<=n;i++){
             int t,r;
             scanf("%d%d",&t,&r);
             a[t]=r;
         }
         q[] = ;
         int f = ;
         for(int i=;i<=n;i++){
             if(a[i]>a[i-]){
                 q[f++]=a[i];
             }
             else{
                 int t = BinSearch(f-,,a[i]);
                 q[t] = a[i];

             }
             /*
             for(int j=1;j<f;j++)
                 cout<<q[j]<<' ';
             cout<<endl;
             */
         }
         cout<<"Case "<<num++<<':'<<endl;
         if(f-==)
             cout<<"My king, at most "<<f-<<" road can be built."<<endl;
         else
             cout<<"My king, at most "<<f-<<" roads can be built."<<endl;
         cout<<endl;
     }
     return ;
 } 

 #include <iostream>
 #include <stdio.h>
 using namespace std;
 int a[];
 int q[];
 int BinSearch(int n)    //二分查找
 {
     int len = ;
     q[] = a[];
     for(int i=;i<=n;i++){
         int l=,r=len;
         while(l<=r){
             int mid = (l+r)/;
             if(a[i]<=q[mid])
                 r=mid-;
             else
                 l=mid+;
         }
         q[l] = a[i];
         if(l>len)
             len=l;
     }
     return len;
 }
 int main()
 {
     int n,num=;
     while(cin>>n){
         for(int i=;i<=n;i++){
             int t,r;
             scanf("%d%d",&t,&r);
             a[t]=r;
         }

         int len = BinSearch(n);

         cout<<"Case "<<num++<<':'<<endl;
         if(len==)
             cout<<"My king, at most "<<len<<" road can be built."<<endl;
         else
             cout<<"My king, at most "<<len<<" roads can be built."<<endl;
         cout<<endl;
     }
     return ;
 } 

Freecode : www.cnblogs.com/yym2013