【ML数学知识】极大似然估计

它是建立在极大似然原理的基础上的一个统计方法，极大似然原理的直观想法是，一个随机试验如有若干个可能的结果A，B，C，... ，若在一次试验中，结果A出现了，那么可以认为实验条件对A的出现有利，也即出现的概率P(A)较大。极大似然原理的直观想法我们用下面例子说明。设甲箱中有99个白球，1个黑球；乙箱中有1个白球．99个黑球。现随机取出一箱，再从抽取的一箱中随机取出一球，结果是黑球，这一黑球从乙箱抽取的概率比从甲箱抽取的概率大得多，这时我们自然更多地相信这个黑球是取自乙箱的。一般说来，事件A发生的概率与某一未知参数  
有关，  
取值不同，则事件A发生的概率  
也不同，当我们在一次试验中事件A发生了，则认为此时的  
值应是t的一切可能取值中使  
达到最大的那一个，极大似然估计法就是要选取这样的t值作为参数t的估计值，使所选取的样本在被选的总体中出现的可能性为最大。 [1] 
极大似然估计，只是一种概率论在统计学的应用，它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。极大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。
当然极大似然估计只是一种粗略的数学期望，要知道它的误差大小还要做区间估计。   -----百度百科

转自：https://blog.csdn.net/yanqingan/article/details/6125812

1. 作用

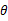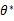在已知试验结果（即是样本）的情况下，用来估计满足这些样本分布的参数，把可能性最大的那个参数作为真实的参数估计。

2. 离散型

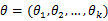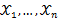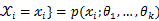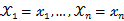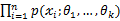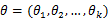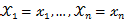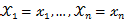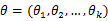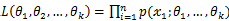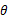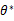设为离散型随机变量，为多维参数向量，如果随机变量相互独立且概率计算式为P{，则可得概率函数为P{}=，在固定时，上式表示的概率；当已知的时候，它又变成的函数，可以把它记为，称此函数为似然函数。似然函数值的大小意味着该样本值出现的可能性的大小，既然已经得到了样本值，那么它出现的可能性应该是较大的，即似然函数的值也应该是比较大的，因而最大似然估计就是选择使达到最大值的那个作为真实的估计。

3. 连续型

设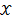为连续型随机变量，其概率密度函数为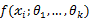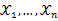，为从该总体中抽出的样本，同样的如果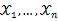相互独立且同分布，于是样本的联合概率密度为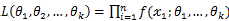。大致过程同离散型一样。

4. 关于概率密度(PDF)

我们来考虑个简单的情况(m=k=1)，即是参数和样本都为1的情况。假设进行一个实验，实验次数定为10次，每次实验成功率为0.2，那么不成功的概率为0.8，用y来表示成功的次数。由于前后的实验是相互独立的，所以可以计算得到成功的次数的概率密度为：

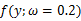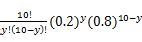= 其中y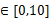

由于y的取值范围已定，而且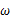也为已知，所以图1显示了y取不同值时的概率分布情况，而图2显示了当时的y值概率情况。

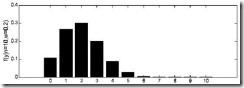
图1 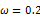时概率分布图

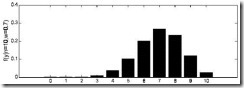
图2 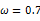时概率分布图

那么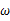在[0,1]之间变化而形成的概率密度函数的集合就形成了一个模型。

5. 最大似然估计的求法

由上面的介绍可以知道，对于图1这种情况y=2是最有可能发生的事件。但是在现实中我们还会面临另外一种情况：我们已经知道了一系列的观察值和一个感兴趣的模型，现在需要找出是哪个PDF（具体来说参数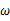为多少时）产生出来的这些观察值。要解决这个问题，就需要用到参数估计的方法，在最大似然估计法中，我们对调PDF中数据向量和参数向量的角色，于是可以得到似然函数的定义为：

该函数可以理解为，在给定了样本值的情况下，关于参数向量取值情况的函数。还是以上面的简单实验情况为例，若此时给定y为7，那么可以得到关于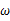的似然函数为：

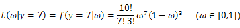
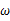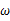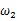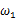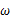继续回顾前面所讲，图1,2是在给定的情况下，样本向量y取值概率的分布情况；而图3是图1,2横纵坐标轴相交换而成，它所描述的似然函数图则指出在给定样本向量y的情况下，符合该取值样本分布的各种参数向量的可能性。若相比于，使得y=7出现的可能性要高，那么理所当然的要比更加接近于真正的估计参数。所以求的极大似然估计就归结为求似然函数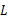的最大值点。那么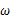取何值时似然函数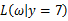最大，这就需要用到高等数学中求导的概念，如果是多维参数向量那么就是求偏导。

图3 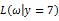的似然函数分布图

主要注意的是多数情况下，直接对变量进行求导反而会使得计算式子更加的复杂，此时可以借用对数函数。由于对数函数是单调增函数，所以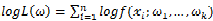与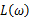具有相同的最大值点，而在许多情况下，求的最大值点比较简单。于是，我们将求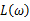的最大值点改为求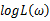的最大值点。

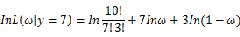
若该似然函数的导数存在，那么对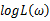关于参数向量的各个参数求导数（当前情况向量维数为1），并命其等于零，得到方程组：

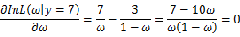
可以求得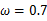时似然函数有极值，为了进一步判断该点位最大值而不是最小值，可以继续求二阶导来判断函数的凹凸性，如果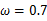的二阶导为负数那么即是最大值，这里再不细说。

还要指出，若函数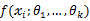关于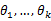的导数不存在，我们就无法得到似然方程组，这时就必须用其它的方法来求最大似然估计值，例如用有界函数的增减性去求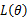的最大值点

6. 总结

最大似然估计，只是一种概率论在统计学的应用，它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。最大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。

求最大似然函数估计值的一般步骤： 
（1） 写出似然函数
（2） 对似然函数取对数，并整理
（3） 求导数
（4） 解似然方程

对于最大似然估计方法的应用，需要结合特定的环境，因为它需要你提供样本的已知模型进而来估算参数，例如在模式识别中，我们可以规定目标符合高斯模型。而且对于该算法，我理解为，“知道”和“能用”就行，没必要在程序设计时将该部分实现，因为在大多数程序中只会用到我最后推导出来的结果。个人建议，如有问题望有经验者指出。在文献^[1]中讲解了本文的相关理论内容，在文献^[2]附有3个推导例子。

7. 参考文献

[1]I.J. Myung. Tutorial on maximum likelihood estimation[J]. Journal of Mathematical Psychology, 2003, 90-100.

[2] http://edu6.teacher.com.cn/ttg006a/chap7/jiangjie/72.htm

该文通过Windows Live Writer上传，如有版面问题影响视觉效果请见谅，可以通过点击看清晰图！^0^