聚类算法——MCL
最近在看聚类方面的论文,接触到了MCL聚类,在网上找了许久,没什么中文的资料,可能写的最具体的便是GatsbyNewton写的 马尔可夫聚类算法(MCL) 这篇博客了。但是,其中仍有一些不详细的地方。而MCL这一方法是在作者在其博士论文中提出的,篇幅太长,难以细读,也不适合作为用来学习MCL这一算法的文献。找来找去,终于找到一篇可以看的PDF文档,但每中不足的是此文档是英文的。趁此机会,结合上述材料,总结了一下MCL的基本思想,也为了往个人博客里添加些实质性的内容,便整理了这一文档。文章中可能会有不对的地方,希望大家相互交流 。◕‿◕。
Background
Different Clustering
Vector Clustering
我们在描述一个人时,常常会使用他所拥有的特点来表示,比如说:张三,男,高个子,有点壮。那么,这就可以用四维向量来表示,如果再复杂一些,就是更高维的向量空间了。下图是在二维空间之中的分布情况,可以较为直观的看出,以红色虚线为界,可以分为两个类别。

Graph Clustering
和特征聚类不同,图聚类比较难以观察,整个算法以各点之间的距离作为突破口,可以这样形容:张三,是王五的好朋友,刚认识李四,对赵六很是反感。那么,对于该节点,我们无法直接得出他的特征,但能知道他的活动圈。利用图聚类,可以将同一社交范围的人聚合到一起。MCL就是属于图聚类的一种。
Random Walks
首先看下图:

从图中,我们可以看到,不同的簇,应当具有以下的特点:
- 位于同一簇的点,其内部的联系应当紧密,而和外部的联系则比较少(惺惺相惜)
也就是说:如果你从一个点出发,到达其中的一个邻近点,那么你在簇内的可能性远大于离开当前簇,到达新簇的可能性——这就是MCL的核心思想。如果在一张图上进行多次的“Random Walks”,那么就有很大可能发现簇群,达到聚类的目的。而“Random Walks”的实现则是通过“Markov Chains”(马尔柯夫链)。
Markov Chains
为了说明 Markov Chain ,我们使用如下的简单例子:
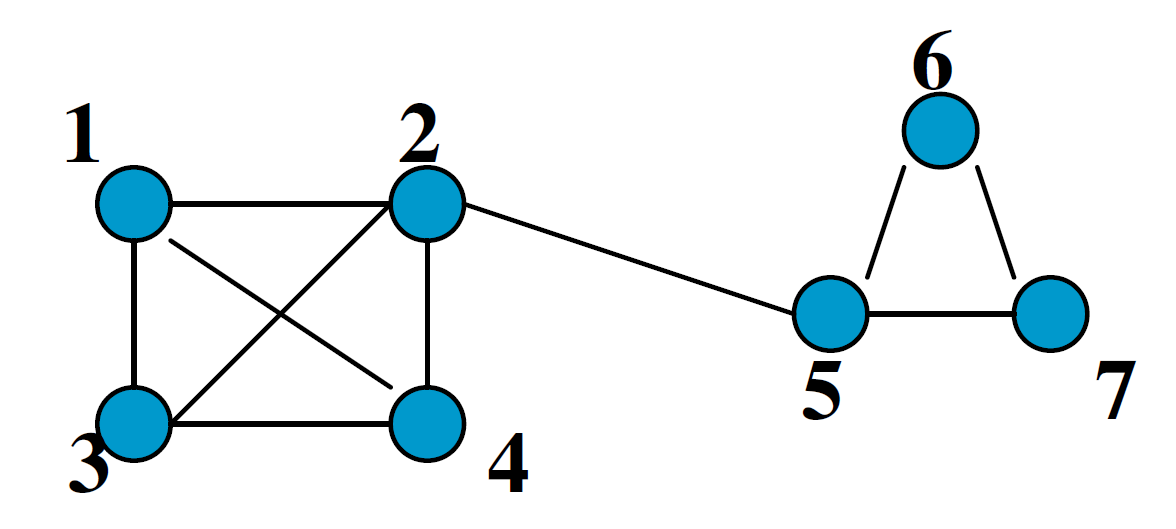
在此图中,我们可以分为两个子图:\(V(1,2,3,4)\)和\(V(5,6,7)\),其中,\(V_1\)是一簇,\(V_2\)是另一簇。在同一簇群中,各点之间完全连接,在不同簇之间,仅有\((2,5)\)一条边。
- 现在,我们从\(V_1\)出发,假设每条边都一样,那么则一步之后我们有\(1/3\)的概率到达\(V_2\),\(1/3\)的概率到达\(V_3\),\(1/3\)的概率到达\(V_4\),同时,有0的概率到达\(V_5,V_6,V_7\)。
- 对于\(V_2\),则有\(1/4\)的概率到达\(V_1,V_3,V_4,V_5\),有0的概率到达\(V_6,V_7\)。
通过计算每个点到达其余点的概率,我们可以得到如下的概率矩阵:
\[
P =
\left[
\matrix{
0 & .25 & .33 & .33 & 0 & 0 & 0 \cr
.33 & 0 & .33 & .33 & .33 & 0 & 0 \cr
.33 & .25 & 0 & .33 & 0 & 0 & 0 \cr
.33 & .25 & .33 & 0 & 0 & 0 & 0 \cr
0 & .25 & 0 & 0 & 0 & .5 & .5 \cr
0 & 0 & 0 & 0 & .33 & 0 & .5 \cr
0 & 0 & 0 & 0 & .33 & .5 & 0
}
\right]
\]
为了计算简单,我们使用一个更简单的矩阵进行接下来的说明:
\[
P_1 =
\left[
\matrix{
.6 & .2 \cr
.4 & .8
}
\right]
\]
这表示的是从任意点出发,经过一步之后到达其它点的概率矩阵,那么,经过两次之后、三次以及最终的概率矩阵为:
\[
P_2 = P_1P_1
\left[
\matrix{
.44 & .28 \cr
.56 & .72
}
\right]
\\
P_3 = P_2P_1
\left[
\matrix{
.35 & .32 \cr
.65 & .68
}
\right]
\\
\vdots
\\
P_n =
\left[
\matrix{
.33 & .33 \cr
.66 & .66
}
\right]
\]
根据上述例子,我们已经接触到了 Markov Chain ,那么现在就给其下一个定义:
Markov Process——在给定当前知识或信息的情况下,过去(即当期以前的历史状态)对于预测将来(即当期以后的未来状态)是无关的。
Markov Chain——如果有由随机变量\(X_1,X_2,X_3\cdots\)组成的数列。这些变量的范围,即他们所有可能取值的集合,被称为“状态空间”。而\(X_n\)的值则是在时间\(n\)的状态,如果\(X_{n+1}\)对于过去状态的条件概率分布满足:\(P(X_{n+1} = x | X_0,X_1,X_2,\cdots,X_n) = P(X_{n+1} = x | X_n)\),则我们称其是一条Markov Chain
Weighted Graphs
之前的例子中,图的边是没有权值的,也就是所有的边都是一样的。现在,为每条边添加一个权重(可以理解为亲密程度),那么,就需要重新计算到达每个点的概率了。
假设有如下的图:
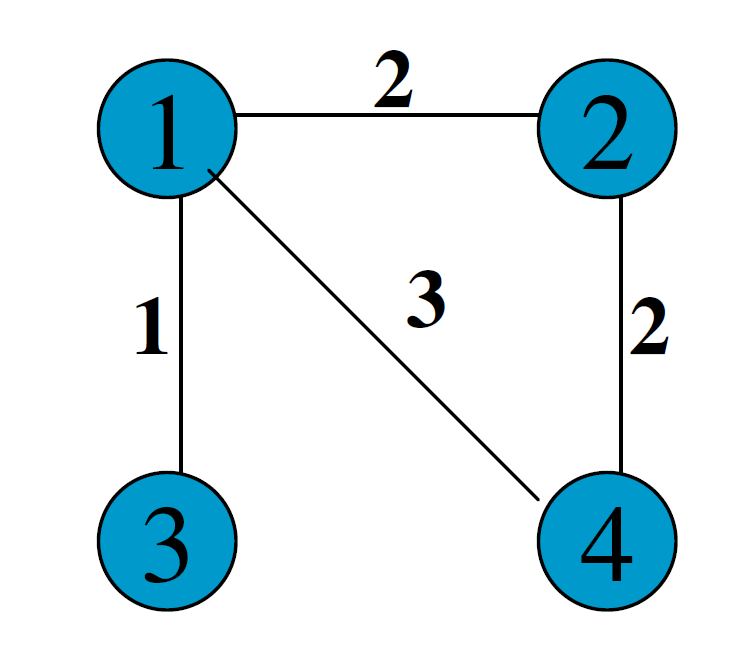
那么,其概率矩阵怎么计算?
首先,我们要计算得到邻接矩阵,即:
\[
edge =
\left[
\matrix{
0 & 2 & 1 & 3 \cr
2 & 0 & 0 & 2 \cr
1 & 0 & 0 & 0 \cr
3 & 2 & 0 & 0
}
\right]
\]
通过邻接矩阵,我们就可以计算得到概率矩阵了,具体计算公式如下:
\[
P_{ij}=\frac{edge_{ij}}{\sum\limits_{i=1}^{n}{edge_{ij}}}
\]
最后的概率矩阵如下:
\[
P =
\left[
\matrix{
0 & 1/2 & 1 & 3/5 \cr
1/3 & 0 & 0 & 2/5 \cr
1/6 & 0 & 0 & 0\cr
1/2 & 1/2 & 0 & 0
}
\right]
\]
之后的计算相同。
Self Loops
在上述的例子中均未考虑一个重要的问题,我们先来看一个例子:
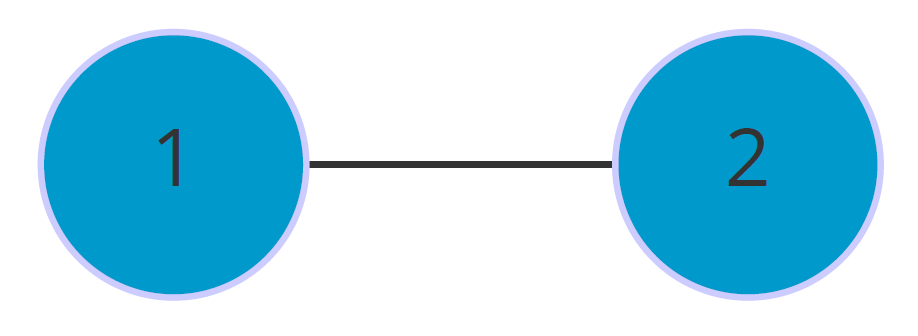
很简单,就两个点,一条边。那么,它的概率矩阵呢:
\[
P_{odd} =
\left[
\matrix{
0 & 1 \cr
1 & 0 \cr
}
\right]
\\
P_{even} =
\left[
\matrix{
1 & 0 \cr
0 & 1 \cr
}
\right]
\]
仔细观察可以发现,这个概率矩阵不管进行几次计算,都不会收敛,而且,对于\(P_{11}\)和\(P_{22}\)而言,仅在奇数步后到达,在偶数步时,永远不可达。因此,无法进行随机游走(本来它就没有随机项供人选择)
为了解决这个问题,我们可以为其添加自环来消除奇偶幂次带来的影响:
\[
edge =
\left[
\matrix{
1 & 1 \cr
1 & 1 \cr
}
\right]
\\
P =
\left[
\matrix{
.5 & .5\cr
.5 & .5
}
\right]
\]
MCL
Markov Chain Cluster Structure
利用 Random Walks 可以求出最终的概率矩阵,但是,在求的过程中,也丢失了大量的信息。

还是这张图,它的概率矩阵和最终的概率矩阵如下:
\[
P =
\left[
\matrix{
0 & .25 & .33 & .33 & 0 & 0 & 0 \cr
.33 & 0 & .33 & .33 & .33 & 0 & 0 \cr
.33 & .25 & 0 & .33 & 0 & 0 & 0 \cr
.33 & .25 & .33 & 0 & 0 & 0 & 0 \cr
0 & .25 & 0 & 0 & 0 & .5 & .5 \cr
0 & 0 & 0 & 0 & .33 & 0 & .5 \cr
0 & 0 & 0 & 0 & .33 & .5 & 0
}
\right]
\Longrightarrow
\left[
\matrix{
.15 & .15 & .15 & .15 & .15 & .15 & .15 \cr
.2 & .2 & .2 & .2 & .2 & .2 & .2 \cr
.15 & .15 & .15 & .15 & .15 & .15 & .15 \cr
.15 & .15 & .15 & .15 & .15 & .15 & .15 \cr
.15 & .15 & .15 & .15 & .15 & .15 & .15\cr
.1 & .1 & .1 & .1 & .1 & .1 & .1\cr
.1 & .1 & .1 & .1 & .1 & .1 & .1 &
}
\right]
\]
从最终的矩阵可以看出,其最终概率和起始点的位置无关!对于聚类,这并不是一个好消息,因为我们想要得到的是一个有明显区分度的矩阵来表示不同的类别。因此,我们需要对其进行一定的修改,这也是MCL主要要解决的问题。
Inflation
如果说,前面的内容在介绍 Markov Chain 如何进行 Expansion 的话,那么,现在就添加一个新的过程: Inflation 。这个过程就是为了解决 Expansion 所导致的概率趋同问题的。
简单的说,Inflation 就是将概率矩阵中的每个值进行了一次幂次扩大,这样就能使得强化紧密的点,弱化松散的点。(强者恒强,弱者恒弱)
假设有矩阵\(M^{k \times l}\),和一个给定的非负实数\(r\),经过 Inflation 强化后的矩阵为\(\Gamma_rM\),那么它的强化公式如下:
\[
(\Gamma_rM)_{pq} = (M_{pq})^r / \sum\limits_{i=1}^k (M_{pq})^r
\]
为了更直观的说明,我们来看下面的一个例子:
\[
A =
\left[
\matrix{
0 \cr
1/2 \cr
0 \cr
1/6 \cr
1/3
}
\right]
\]
在 Inflation 之前,向量\(A\) 就是一个正常的概率向量。为了令其具有更明显的区分度,对其进行 Inflation 强化。
假设\(r\)的取值为2,\(A^2\)如下:
\[
A^2 =
\left[
\matrix{
0 \cr
1/4 \cr
0 \cr
1/36 \cr
1/9
}
\right]
\]
对该向量进行标准化,保证\(\sum\limits_{i=1}^n A_i = 1\)。
\[
\Gamma_rA =
\left[
\matrix{
0 \cr
9/14 \cr
0 \cr
1/14 \cr
4/14
}
\right]
\]
可以看出,进过一次变换后,区分度进一步的增加,这就为之后的聚类提供了保证。在这里要注明的是Inflation 的参数\(r\)会影响聚簇的粒度,这个在之后会有说明。
MCL Algorithm
在MCL中, Expansion 和 Inflation 将不断的交替进行,Expansion 使得不同的区域之间的联系加强,而 Inflation 则不断的分化各点之间的联系。经过多次迭代,将渐渐出现聚集现象,以此便达到了聚类的效果。
MCL的算法流程具体如下:
- 输入:一个非全连通图,Expansion 时的参数\(e\)和 Inflation 的参数\(r\)。
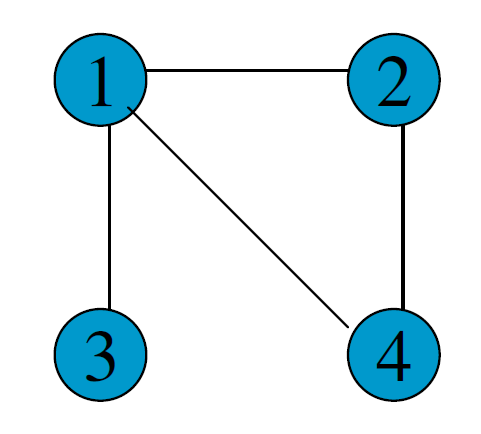
\[
e = 2, r = 2
\]
建立邻接矩阵
\[
edge =
\left[
\matrix{
0 & 1 & 1 & 1 \cr
1 & 0 & 0 & 1 \cr
1 & 0 & 0 & 0 \cr
1 & 1 & 0 & 0
}
\right]
\]添加自环
\[
edge' =
\left[
\matrix{
1 & 1 & 1 & 1 \cr
1 & 1 & 0 & 1 \cr
1 & 0 & 1 & 0 \cr
1 & 1 & 0 & 1
}
\right]
\]
标准化概率矩阵
\[
P_0 =
\left[
\matrix{
1/4 & 1/3 & 1/2 & 1/3 \cr
1/4 & 1/3 & 0 & 1/3 \cr
1/4 & 0 & 1/2 & 0 \cr
1/4 & 1/3 & 0 & 1/3
}
\right]
\]Expansion操作,每次对矩阵进行\(e\)次幂方
\[
P_1 = P_0P_0 =
\left[
\matrix{
.35 & .31 & .38 & .31 \cr
.23 & .31 & .13 & .31 \cr
.19 & .08 & .38 & .08 \cr
.23 & .31 & .13 & .31
}
\right]
\]Inflation操作,每次对矩阵内元素进行r次幂方,再进行标准化
\[
P_1' =
\left[
\matrix{
.13 & .09 & .14 & .09 \cr
.05 & .09 & .02 & .09 \cr
.04 & .01 & .14 & .01 \cr
.05 & .09 & .02 & .09
}
\right]
\\
\Gamma_rP_1 =
\left[
\matrix{
.47 & .33 & .45 & .33 \cr
.20 & .33 & .05 & .33 \cr
.13 & .02 & .45 & .02 \cr
.20 & .33 & .05 & .33
}
\right]
\]重复步骤5和6,直到达到稳定
将结果矩阵转化为聚簇
MCL Algorithm Convergence
在作者的论文中,并没有证明MCL算法的收敛性。但是,在实验过程中,总是能够达到最终的收敛状态。下图是一个达到收敛的例子:

为了方便区分不同聚簇,我们将图上的点分为两类:Attractor 和 Vertex 。Attractor 代表了那些有着主导地位的点,这些点吸引着其它的点,将它们牢牢的聚集在周围;Vertex 则表示那些被吸引的点,它们没有主导地位,被 Attractor 所吸引着。其中,Attractor 所在的行必须至少有一个正值,聚集着它所在行中所有正值的点。可以看出,在这个例子中,总共有三个聚簇:{1,6,7,10},{2,3,5},{4,8,9,11,12}。
当然,在MCL中也会存在着重叠的聚簇。如下图,当且仅当簇与簇是同构的时才出现一个点被多个聚簇所吸引。

Inflation Parameter
在之前有提到过Inflation 参数会对聚簇产生影响。一般的,随着\(r\)的增大,其粒度将减小。
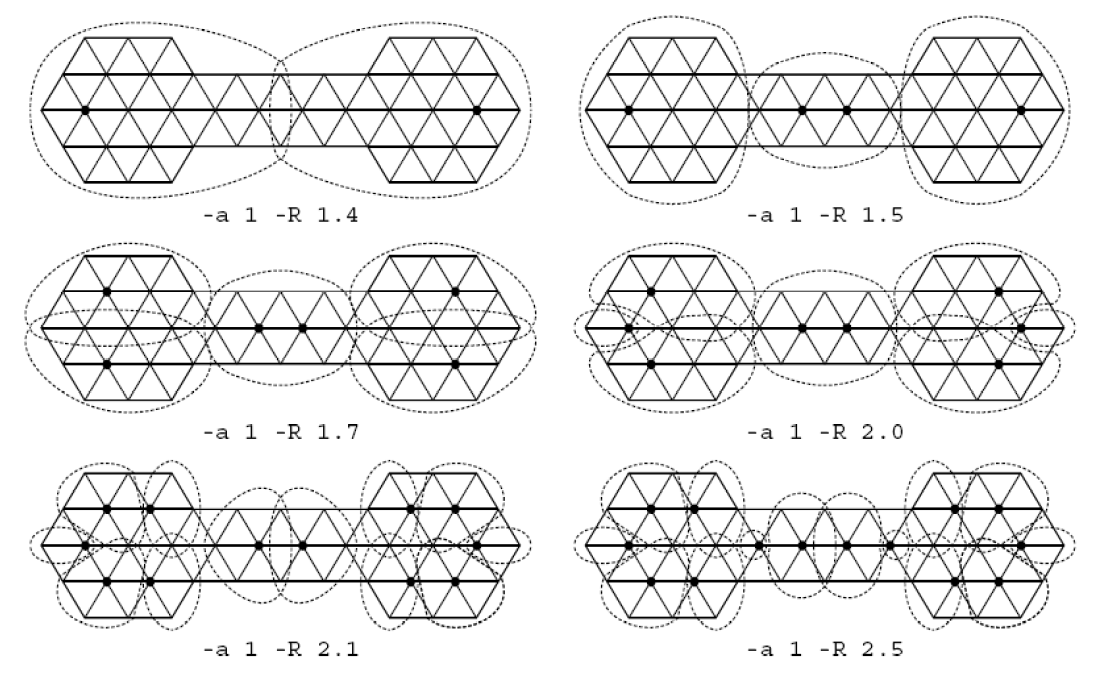
从上图中还可以看出,聚簇的多少和\(e\)有着很大的关系,在大直径的图中就更为明显了。因为偏远地区的点和簇群中心的联系越来越少,便很可能出现“挖墙脚”的可能,以及簇群内部分化问题。
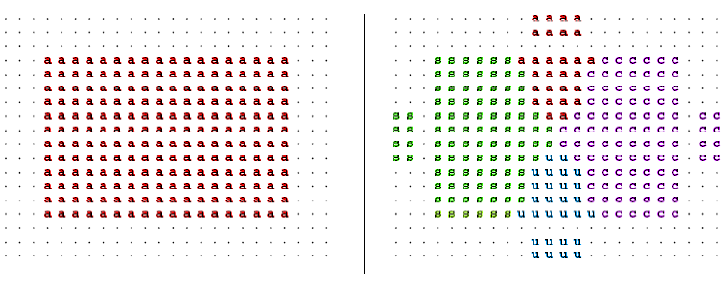
Analysis of MCL
MCL有着较为优良的性能,总的来说,它的优缺点如下:
- 随着图大小的扩张,MCL有着良好的刻度
- 可以在有权或无权的图上运行
- 最后的聚类结果令人满意
- 可以较好的处理噪声数据
不需要人为规定簇群数量,而是可以根据参数自行确定
- 不能发现发生重叠的点
不适合在大图上使用(它的算法复杂度是\(O(N^3)\))
以上是我对MCL的一些总结看法,欢迎大家来和我交流讨论。
聚类算法——MCL的更多相关文章
- DBSCAN密度聚类算法
DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法)是一种很典型的密度聚类算法,和K-M ...
- 基于改进人工蜂群算法的K均值聚类算法(附MATLAB版源代码)
其实一直以来也没有准备在园子里发这样的文章,相对来说,算法改进放在园子里还是会稍稍显得格格不入.但是最近邮箱收到的几封邮件让我觉得有必要通过我的博客把过去做过的东西分享出去更给更多需要的人.从论文刊登 ...
- 挑子学习笔记:两步聚类算法(TwoStep Cluster Algorithm)——改进的BIRCH算法
转载请标明出处:http://www.cnblogs.com/tiaozistudy/p/twostep_cluster_algorithm.html 两步聚类算法是在SPSS Modeler中使用的 ...
- K-Means 聚类算法
K-Means 概念定义: K-Means 是一种基于距离的排他的聚类划分方法. 上面的 K-Means 描述中包含了几个概念: 聚类(Clustering):K-Means 是一种聚类分析(Clus ...
- BIRCH聚类算法原理
在K-Means聚类算法原理中,我们讲到了K-Means和Mini Batch K-Means的聚类原理.这里我们再来看看另外一种常见的聚类算法BIRCH.BIRCH算法比较适合于数据量大,类别数K也 ...
- K-Means聚类算法原理
K-Means算法是无监督的聚类算法,它实现起来比较简单,聚类效果也不错,因此应用很广泛.K-Means算法有大量的变体,本文就从最传统的K-Means算法讲起,在其基础上讲述K-Means的优化变体 ...
- FCM聚类算法介绍
FCM算法是一种基于划分的聚类算法,它的思想就是使得被划分到同一簇的对象之间相似度最大,而不同簇之间的相似度最小.模糊C均值算法是普通C均值算法的改进,普通C均值算法对于数据的划分是硬性的,而FCM则 ...
- 机器学习——利用K-均值聚类算法对未标注数据分组
聚类是一种无监督的学习,它将相似的对象归到同一簇中.它有点像全自动分类.聚类方法几乎可以应用到所有对象,簇内的对象越相似,聚类的效果越好. K-均值(K-means)聚类算法,之所以称之为K-均值是因 ...
- K-均值聚类算法
K-均值聚类算法 聚类是一种无监督的学习算法,它将相似的数据归纳到同一簇中.K-均值是因为它可以按照k个不同的簇来分类,并且不同的簇中心采用簇中所含的均值计算而成. K-均值算法 算法思想 K-均值是 ...
随机推荐
- Python中的编码与解码(转)
Python中的字符编码与解码困扰了我很久了,一直没有认真整理过,这次下静下心来整理了一下我对方面知识的理解. 文章中对有些知识没有做深入的探讨,一是我自己也没有去深入的了解,例如各种编码方案的实现方 ...
- python发送邮件的2种方式
发送邮件的2种方式1.匿名发送 smtpObj = smtplib.SMTP(host, port) smtpObj.sendmail(from_addr, to_addrs, message.as_ ...
- Linux cp命令
cp命令(copy),用来对一个或多个文件,目录进行拷贝 1.语法 cp [选项] [参数] 2.命令选项 -b 当文件存在时,覆盖前,为其创建一个备份-d 当复制软连接时,把目标文件或目录也建立为软 ...
- robotium原理之获取WebElement元素
版权声明:本文为博主原创文章,未经博主同意不得转载. https://blog.csdn.net/hunterno4/article/details/35569665 robotium ...
- Android Volley全然解析(四),带你从源代码的角度理解Volley
版权声明:本文出自郭霖的博客,转载必须注明出处. https://blog.csdn.net/sinyu890807/article/details/17656437 转载请注明出处:http://b ...
- Flask系列(十一)整合Flask中的目录结构(sqlalchemy-utils)
一.SQLAlchemy-Utils 由于sqlalchemy中没有提供choice方法,所以借助SQLAlchemy-Utils组件提供的choice方法 import datetime from ...
- ffmpeg,rtmpdump和nginx rtmp实现录屏,直播和录制
公司最近在做视频直播的项目,我这里分配到对直播的视频进行录制,录制的方式是通过rtmpdump对rtmp的视频流进行录制 前置的知识 ffmpeg: 用于实现把录屏工具发出的视频和音频流,转换成我们需 ...
- 玩转DOM遍历——用NodeIterator实现getElementById,getElementsByTagName方法
先声明一下DOM2中NodeIterator和TreeWalker这两类型真的只是用来玩玩的,因为性能不行遍历起来超级慢,在JS中基本用不到它们,除了<高程>上有两三页对它的讲解外,谷歌的 ...
- ambari关于ranger的一个大坑----端口永远是3306,需要手动修改
ambari关于ranger的一个大坑----端口永远是3306 这个坑是我在搭建ambari环境的时候发现的,我并没有找到原因,求助同事,然后一步步循着蛛丝马迹和试探,终于解决了,然而也揭露了amb ...
- C语言中const和数组
C语言中const的用法 const:在定义变量时,如果使用关键字const,那就表示限制这个变量值不允许被改变. (1) 修饰变量 const离谁越近,谁的值就不能改变. int const ...
