多重检验_LSD方法不准确性
python机器学习-乳腺癌细胞挖掘（博主亲自录制视频）
https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share
机器学习，统计项目联系：QQ231469242
#mental
group1=[2,2,3,4,4,5,3,4,4,4]
#physical
group2=[4,4,3,5,4,1,1,2,3,3]
#medical
group3=[1,2,2,2,3,2,3,1,3,1]
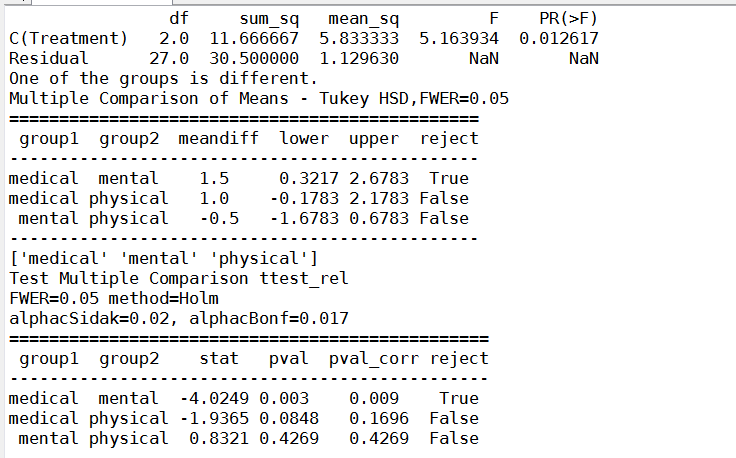
多重检验结果和贾俊平的LSD结果不一样，经过T配对试验，多重检验和T配对试验一致，LSD对小样本可能不准确
# -*- coding: utf-8 -*- # Import standard packages
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import pandas as pd
import os
# additional packages
import sys
sys.path.append(os.path.join('..', '..', 'Utilities')) try:
# Import formatting commands if directory "Utilities" is available
from ISP_mystyle import showData except ImportError:
# Ensure correct performance otherwise
def showData(*options):
plt.show()
return # Other required packages
from statsmodels.stats.multicomp import (pairwise_tukeyhsd,
MultiComparison)
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
from statsmodels.stats.libqsturng import psturng def setData():
''' Set up the data, as a structured array. ''' # The first and last field are 32-bit intergers; the second field is an
# 8-byte string. Note that here we can also give names to the individual
# fields!
data = np.rec.array([
( 1, 'mental', 2 ),
( 2, 'mental', 2 ),
( 3, 'mental', 3 ),
( 4, 'mental', 4 ),
( 5, 'mental', 4 ),
( 6, 'mental', 5 ),
( 7, 'mental', 3 ),
( 8, 'mental', 4 ),
( 9, 'mental', 4 ),
( 10, 'mental', 4 ),
( 11, 'physical', 4 ),
( 12, 'physical', 4 ),
( 13, 'physical', 3 ),
( 14, 'physical', 5 ),
( 15, 'physical', 4 ),
( 16, 'physical', 1 ),
( 17, 'physical', 1 ),
( 18, 'physical', 2 ),
( 19, 'physical', 3 ),
( 20, 'physical', 3 ),
( 21, 'medical', 1 ),
( 22, 'medical', 2 ),
( 23, 'medical', 2 ),
( 24, 'medical', 2 ),
( 25, 'medical', 3 ),
( 26, 'medical', 2 ),
( 27, 'medical', 3 ),
( 28, 'medical', 1 ),
( 29, 'medical', 3 ),
( 30, 'medical', 1 )], dtype=[('idx', '<i4'),
('Treatment', '|S8'),
('StressReduction', '<i4')])
return data def doAnova(data):
'''one-way ANOVA''' df = pd.DataFrame(data)
model = ols('StressReduction ~ C(Treatment)',df).fit() anovaResults = anova_lm(model)
print(anovaResults)
if anovaResults['PR(>F)'][0] < 0.05:
print('One of the groups is different.') def doTukey(data, multiComp):
'''Do a pairwise comparison, and show the confidence intervals''' print((multiComp.tukeyhsd().summary())) # Calculate the p-values:
res2 = pairwise_tukeyhsd(data['StressReduction'], data['Treatment'])
df = pd.DataFrame(data)
numData = len(df)
numTreatments = len(df.Treatment.unique())
dof = numData - numTreatments # Show the group names
print((multiComp.groupsunique)) # Generate a print ------------------- # Get the data
xvals = np.arange(3)
res2 = pairwise_tukeyhsd(data['StressReduction'], data['Treatment'])
errors = np.ravel(np.diff(res2.confint)/2) # Plot them
plt.plot(xvals, res2.meandiffs, 'o')
plt.errorbar(xvals, res2.meandiffs, yerr=errors, fmt='o') # Put on labels
pair_labels = multiComp.groupsunique[np.column_stack(res2._multicomp.pairindices)]
plt.xticks(xvals, pair_labels) # Format the plot
xlim = -0.5, 2.5
plt.hlines(0, *xlim)
plt.xlim(*xlim)
plt.title('Multiple Comparison of Means - Tukey HSD, FWER=0.05' +
'\n Pairwise Mean Differences') # Save to outfile, and show the data
outFile = 'multComp.png'
showData(outFile) def Holm_Bonferroni(multiComp):
''' Instead of the Tukey's test, we can do pairwise t-test ''' # First, with the "Holm" correction
rtp = multiComp.allpairtest(stats.ttest_rel, method='Holm')
print((rtp[0])) # and then with the Bonferroni correction
print((multiComp.allpairtest(stats.ttest_rel, method='b')[0])) # Any value, for testing the program for correct execution
checkVal = rtp[1][0][0,0]
return checkVal def main():
# Get the data
data = setData() # Do a one-way ANOVA
doAnova(data) #Then, do the multiple testing
multiComp = MultiComparison(data['StressReduction'], data['Treatment']) doTukey(data, multiComp) # Tukey's HSD test
checkVal = Holm_Bonferroni(multiComp) # Alternatives to Tukey's HSD test return checkVal # this is only for regression testing of the program if __name__ == '__main__':
main()
多重检验结果和贾俊平的LSD结果不一样，经过T配对试验，多重检验和T配对试验一致，LSD对小样本可能不准确
# -*- coding: utf-8 -*- import scipy,math
from scipy.stats import f
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# additional packages
from statsmodels.stats.diagnostic import lillifors
#多重比较
from statsmodels.sandbox.stats.multicomp import multipletests
#用于排列组合
import itertools
#独立T检验
from scipy.stats import ttest_ind
#配对T检验
from scipy.stats import ttest_rel #mental
group1=[2,2,3,4,4,5,3,4,4,4]
#physical
group2=[4,4,3,5,4,1,1,2,3,3]
#medical
group3=[1,2,2,2,3,2,3,1,3,1] list_groups=[group1,group2,group3]
list_total=group1+group2+group3
a=0.05 #one within group error,also know as random error
def SE(group):
se=0
mean1=np.mean(group)
for i in group:
error=i-mean1
se+=error**2
return se '''
>>> SE(group1)
22.0
>>> SE(group2)
18.0
>>> SE(group3)
14.0
'''
#sum of squares within group error,also know as random error
def SSE(list_groups):
sse=0
for group in list_groups:
se=SE(group)
sse+=se
return sse #误差总平方和
def SST(list_total):
sst=0
mean1=np.mean(list_total)
for i in list_total:
error=i-mean1
sst+=error**2
return sst #SSA,between-group sum of squares 组间平方和,公式1：ssa=sst-sse
def SSA(list_groups,list_total):
sse=SSE(list_groups)
sst=SST(list_total)
ssa=sst-sse
return ssa #SSA,between-group sum of squares 组间平方和
def SSA1(list_groups,list_total):
mean_total=np.mean(list_total)
ssa=0
for group in list_groups:
group_mean=np.mean(group)
distance=(mean_total-group_mean)**2
ssa+=distance ssa=ssa*5
return ssa #处理效应均方
def MSA(list_groups,list_total):
ssa=SSA(list_groups,list_total)
msa=ssa/(len(list_groups)-1)*1.0
return msa # 误差均方
def MSE(list_groups,list_total):
sse=SSE(list_groups)
mse=sse/(len(list_total)-1*len(list_groups))*1.0
return mse #F score
def F(list_groups,list_total):
msa=MSA(list_groups,list_total)
mse=MSE(list_groups,list_total)
ratio=msa/mse*1.0
return ratio
'''
>>> F(list_groups,list_total)
22.592592592592595
''' #LSD检验有问题，需要核对，不如配对T检验准确
#LSD(least significant difference)最小显著差异
def LSD(list_groups,list_total,sample1,sample2):
mean1=np.mean(sample1)
mean2=np.mean(sample2)
distance=abs(mean1-mean2)
print"distance:",distance
#t检验的自由度
df=len(list_total)-1*len(list_groups)
mse=MSE(list_groups,list_total)
print"MSE:",mse
t_value=stats.t(df).isf(a/2)
print"t value:",t_value
lsd=t_value*math.sqrt(mse*(1.0/len(sample1)+1.0/len(sample2)))
print "LSD:",lsd
if distance<lsd:
print"no significant difference between:",sample1,sample2
else:
print"there is significant difference between:",sample1,sample2 #正态分布测试
def check_normality(testData): #20<样本数<50用normal test算法检验正态分布性
if 20<len(testData) <50:
p_value= stats.normaltest(testData)[1]
if p_value<0.05:
print"use normaltest"
print "data are not normal distributed"
return False
else:
print"use normaltest"
print "data are normal distributed"
return True #样本数小于50用Shapiro-Wilk算法检验正态分布性
if len(testData) <50:
p_value= stats.shapiro(testData)[1]
if p_value<0.05:
print "use shapiro:"
print "data are not normal distributed"
return False
else:
print "use shapiro:"
print "data are normal distributed"
return True if 300>=len(testData) >=50:
p_value= lillifors(testData)[1]
if p_value<0.05:
print "use lillifors:"
print "data are not normal distributed"
return False
else:
print "use lillifors:"
print "data are normal distributed"
return True if len(testData) >300:
p_value= stats.kstest(testData,'norm')[1]
if p_value<0.05:
print "use kstest:"
print "data are not normal distributed"
return False
else:
print "use kstest:"
print "data are normal distributed"
return True #对所有样本组进行正态性检验
def NormalTest(list_groups):
for group in list_groups:
#正态性检验
status=check_normality(group1)
if status==False :
return False #排列组合函数
def Combination(list_groups):
combination= []
for i in range(1,len(list_groups)+1):
iter = itertools.combinations(list_groups,i)
combination.append(list(iter))
#需要排除第一个和最后一个
return combination[1:-1][0]
'''
Out[57]:
[[([2, 3, 7, 2, 6], [10, 8, 7, 5, 10]),
([2, 3, 7, 2, 6], [10, 13, 14, 13, 15]),
([10, 8, 7, 5, 10], [10, 13, 14, 13, 15])]]
''' #多重比较
def Multiple_test(list_groups): combination=Combination(list_groups)
for pair in combination:
LSD(list_groups,list_total,pair[0],pair[1]) #discriptive statistcs
print "discriptive statistcs----------------------------------------------"
print "group1 mean",np.mean(group1)
print "group2 mean",np.mean(group2)
print "group3 mean",np.mean(group3) #对所有样本组进行正态性检验
print"M=Normality test:-----------------------------------"
NormalTest(list_groups) #方差齐性检测
print"levene test:-----------------------------------"
leveneResult=scipy.stats.levene(group1,group2,group3)
leveneScore=leveneResult[0]
p_levene=leveneResult[1]
if p_levene<0.05:
print"levene test is not fit,be attention!"
else:
print"levene test is ok"
'''
H0成立，三组数据方差无显著差异
Out[9]: LeveneResult(statistic=0.24561403508771934, pvalue=0.7860617221429711)
''' print "result--------------------------------------------------"
f_score=F(list_groups,list_total)
print"F score:",f_score
#sf 为生存函数survival function
#组数自由度
df1=len(list_groups)-1
#所有样本的自由度
df2=len(list_total)-1*len(list_groups)
probability=f.sf(f_score,df1,df2)
print"p value:",probability
'''
Out[28]: 8.5385924542746692e-05
'''
if probability<0.05:
print"there is significance,H1 win"
else:
print"there is no significance,H0 win" #多重比较
print"multiple test----------------------------------------------"
print"Multiple test",Multiple_test
Multiple_test(list_groups)
贾俊平书里的例子，综合多重检验和LSD方法结果一致
#居民区
group1=[265,310,220,290,350,300,445,480,500,430,428,530]
#商业区
group2=[410,305,450,380,310,390,590,480,510,470,415,390]
#写字楼
group3=[180,290,330,220,170,256,290,283,260,246,275,320]
# -*- coding: utf-8 -*- # Import standard packages
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import pandas as pd
import os
# additional packages
import sys
sys.path.append(os.path.join('..', '..', 'Utilities')) try:
# Import formatting commands if directory "Utilities" is available
from ISP_mystyle import showData except ImportError:
# Ensure correct performance otherwise
def showData(*options):
plt.show()
return # Other required packages
from statsmodels.stats.multicomp import (pairwise_tukeyhsd,
MultiComparison)
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
from statsmodels.stats.libqsturng import psturng def setData():
''' Set up the data, as a structured array. ''' # The first and last field are 32-bit intergers; the second field is an
# 8-byte string. Note that here we can also give names to the individual
# fields!
data = np.rec.array([
( 1, 'resident', 265 ),
( 2, 'resident', 310 ),
( 3, 'resident', 220 ),
( 4, 'resident', 290 ),
( 5, 'resident', 350 ),
( 6, 'resident', 300 ),
( 7, 'resident', 445 ),
( 8, 'resident', 480 ),
( 9, 'resident', 500 ),
( 10, 'resident', 430),
( 11, 'resident', 428),
( 12, 'resident', 530 ),
( 13, 'commercial', 410 ),
( 14, 'commercial', 305 ),
( 15, 'commercial', 450 ),
( 16, 'commercial', 380 ),
( 17, 'commercial', 310 ),
( 18, 'commercial', 390 ),
( 19, 'commercial', 590 ),
( 20, 'commercial', 480 ),
( 21, 'commercial', 510 ),
( 22, 'commercial', 470 ),
( 23, 'commercial', 415 ),
( 24, 'commercial', 390 ),
( 25, 'officeBuilding', 180 ),
( 26, 'officeBuilding', 290 ),
( 27, 'officeBuilding', 330 ),
( 28, 'officeBuilding', 220 ),
( 29, 'officeBuilding', 170),
( 30, 'officeBuilding', 256),
( 31, 'officeBuilding', 290 ),
( 32, 'officeBuilding', 283 ),
( 33, 'officeBuilding', 260),
( 34, 'officeBuilding', 246),
( 35, 'officeBuilding', 275),
( 36, 'officeBuilding', 320),
], dtype=[('idx', '<i4'),
('Treatment', '|S8'),
('StressReduction', '<i4')])
return data def doAnova(data):
'''one-way ANOVA''' df = pd.DataFrame(data)
model = ols('StressReduction ~ C(Treatment)',df).fit() anovaResults = anova_lm(model)
print(anovaResults)
if anovaResults['PR(>F)'][0] < 0.05:
print('One of the groups is different.') def doTukey(data, multiComp):
'''Do a pairwise comparison, and show the confidence intervals''' print((multiComp.tukeyhsd().summary())) # Calculate the p-values:
res2 = pairwise_tukeyhsd(data['StressReduction'], data['Treatment'])
df = pd.DataFrame(data)
numData = len(df)
numTreatments = len(df.Treatment.unique())
dof = numData - numTreatments # Show the group names
print((multiComp.groupsunique)) # Generate a print ------------------- # Get the data
xvals = np.arange(3)
res2 = pairwise_tukeyhsd(data['StressReduction'], data['Treatment'])
errors = np.ravel(np.diff(res2.confint)/2) # Plot them
plt.plot(xvals, res2.meandiffs, 'o')
plt.errorbar(xvals, res2.meandiffs, yerr=errors, fmt='o') # Put on labels
pair_labels = multiComp.groupsunique[np.column_stack(res2._multicomp.pairindices)]
plt.xticks(xvals, pair_labels) # Format the plot
xlim = -0.5, 2.5
plt.hlines(0, *xlim)
plt.xlim(*xlim)
plt.title('Multiple Comparison of Means - Tukey HSD, FWER=0.05' +
'\n Pairwise Mean Differences') # Save to outfile, and show the data
outFile = 'multComp.png'
showData(outFile) def Holm_Bonferroni(multiComp):
''' Instead of the Tukey's test, we can do pairwise t-test ''' # First, with the "Holm" correction
rtp = multiComp.allpairtest(stats.ttest_rel, method='Holm')
print((rtp[0])) # and then with the Bonferroni correction
print((multiComp.allpairtest(stats.ttest_rel, method='b')[0])) # Any value, for testing the program for correct execution
checkVal = rtp[1][0][0,0]
return checkVal def main():
# Get the data
data = setData() # Do a one-way ANOVA
doAnova(data) #Then, do the multiple testing
multiComp = MultiComparison(data['StressReduction'], data['Treatment']) doTukey(data, multiComp) # Tukey's HSD test
checkVal = Holm_Bonferroni(multiComp) # Alternatives to Tukey's HSD test return checkVal # this is only for regression testing of the program if __name__ == '__main__':
main()
贾俊平书里的例子，综合多重检验和LSD方法结果一致
#居民区
group1=[265,310,220,290,350,300,445,480,500,430,428,530]
#商业区
group2=[410,305,450,380,310,390,590,480,510,470,415,390]
#写字楼
group3=[180,290,330,220,170,256,290,283,260,246,275,320]
# -*- coding: utf-8 -*- import scipy,math
from scipy.stats import f
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# additional packages
from statsmodels.stats.diagnostic import lillifors
#多重比较
from statsmodels.sandbox.stats.multicomp import multipletests
#用于排列组合
import itertools
#独立T检验
from scipy.stats import ttest_ind
#配对T检验
from scipy.stats import ttest_rel #居民区
group1=[265,310,220,290,350,300,445,480,500,430,428,530]
#商业区
group2=[410,305,450,380,310,390,590,480,510,470,415,390]
#写字楼
group3=[180,290,330,220,170,256,290,283,260,246,275,320] list_groups=[group1,group2,group3]
list_total=group1+group2+group3
a=0.05 #one within group error,also know as random error
def SE(group):
se=0
mean1=np.mean(group)
for i in group:
error=i-mean1
se+=error**2
return se '''
>>> SE(group1)
22.0
>>> SE(group2)
18.0
>>> SE(group3)
14.0
'''
#sum of squares within group error,also know as random error
def SSE(list_groups):
sse=0
for group in list_groups:
se=SE(group)
sse+=se
return sse #误差总平方和
def SST(list_total):
sst=0
mean1=np.mean(list_total)
for i in list_total:
error=i-mean1
sst+=error**2
return sst #SSA,between-group sum of squares 组间平方和,公式1：ssa=sst-sse
def SSA(list_groups,list_total):
sse=SSE(list_groups)
sst=SST(list_total)
ssa=sst-sse
return ssa #SSA,between-group sum of squares 组间平方和
def SSA1(list_groups,list_total):
mean_total=np.mean(list_total)
ssa=0
for group in list_groups:
group_mean=np.mean(group)
distance=(mean_total-group_mean)**2
ssa+=distance ssa=ssa*5
return ssa #处理效应均方
def MSA(list_groups,list_total):
ssa=SSA(list_groups,list_total)
msa=ssa/(len(list_groups)-1)*1.0
return msa # 误差均方
def MSE(list_groups,list_total):
sse=SSE(list_groups)
mse=sse/(len(list_total)-1*len(list_groups))*1.0
return mse #F score
def F(list_groups,list_total):
msa=MSA(list_groups,list_total)
mse=MSE(list_groups,list_total)
ratio=msa/mse*1.0
return ratio
'''
>>> F(list_groups,list_total)
22.592592592592595
''' #LSD检验有问题，需要核对，不如配对T检验准确
#LSD(least significant difference)最小显著差异
def LSD(list_groups,list_total,sample1,sample2):
mean1=np.mean(sample1)
mean2=np.mean(sample2)
distance=abs(mean1-mean2)
print"distance:",distance
#t检验的自由度
df=len(list_total)-1*len(list_groups)
mse=MSE(list_groups,list_total)
print"MSE:",mse
t_value=stats.t(df).isf(a/2)
print"t value:",t_value
lsd=t_value*math.sqrt(mse*(1.0/len(sample1)+1.0/len(sample2)))
print "LSD:",lsd
if distance<lsd:
print"no significant difference between:",sample1,sample2
else:
print"there is significant difference between:",sample1,sample2 #正态分布测试
def check_normality(testData): #20<样本数<50用normal test算法检验正态分布性
if 20<len(testData) <50:
p_value= stats.normaltest(testData)[1]
if p_value<0.05:
print"use normaltest"
print "data are not normal distributed"
return False
else:
print"use normaltest"
print "data are normal distributed"
return True #样本数小于50用Shapiro-Wilk算法检验正态分布性
if len(testData) <50:
p_value= stats.shapiro(testData)[1]
if p_value<0.05:
print "use shapiro:"
print "data are not normal distributed"
return False
else:
print "use shapiro:"
print "data are normal distributed"
return True if 300>=len(testData) >=50:
p_value= lillifors(testData)[1]
if p_value<0.05:
print "use lillifors:"
print "data are not normal distributed"
return False
else:
print "use lillifors:"
print "data are normal distributed"
return True if len(testData) >300:
p_value= stats.kstest(testData,'norm')[1]
if p_value<0.05:
print "use kstest:"
print "data are not normal distributed"
return False
else:
print "use kstest:"
print "data are normal distributed"
return True #对所有样本组进行正态性检验
def NormalTest(list_groups):
for group in list_groups:
#正态性检验
status=check_normality(group1)
if status==False :
return False #排列组合函数
def Combination(list_groups):
combination= []
for i in range(1,len(list_groups)+1):
iter = itertools.combinations(list_groups,i)
combination.append(list(iter))
#需要排除第一个和最后一个
return combination[1:-1][0]
'''
Out[57]:
[[([2, 3, 7, 2, 6], [10, 8, 7, 5, 10]),
([2, 3, 7, 2, 6], [10, 13, 14, 13, 15]),
([10, 8, 7, 5, 10], [10, 13, 14, 13, 15])]]
''' #多重比较
def Multiple_test(list_groups): combination=Combination(list_groups)
for pair in combination:
LSD(list_groups,list_total,pair[0],pair[1]) #discriptive statistcs
print "discriptive statistcs----------------------------------------------"
print "group1 mean",np.mean(group1)
print "group2 mean",np.mean(group2)
print "group3 mean",np.mean(group3) #对所有样本组进行正态性检验
print"M=Normality test:-----------------------------------"
NormalTest(list_groups) #方差齐性检测
print"levene test:-----------------------------------"
leveneResult=scipy.stats.levene(group1,group2,group3)
leveneScore=leveneResult[0]
p_levene=leveneResult[1]
if p_levene<0.05:
print"levene test is not fit,be attention!"
else:
print"levene test is ok"
'''
H0成立，三组数据方差无显著差异
Out[9]: LeveneResult(statistic=0.24561403508771934, pvalue=0.7860617221429711)
''' print "result--------------------------------------------------"
f_score=F(list_groups,list_total)
print"F score:",f_score
#sf 为生存函数survival function
#组数自由度
df1=len(list_groups)-1
#所有样本的自由度
df2=len(list_total)-1*len(list_groups)
probability=f.sf(f_score,df1,df2)
print"p value:",probability
'''
Out[28]: 8.5385924542746692e-05
'''
if probability<0.05:
print"there is significance,H1 win"
else:
print"there is no significance,H0 win" #多重比较
print"multiple test----------------------------------------------"
print"Multiple test",Multiple_test
Multiple_test(list_groups)
python风控评分卡建模和风控常识(博客主亲自录制视频教程)
多重检验_LSD方法不准确性的更多相关文章
- 除了GPS外的4种获得用户地理位置数据的方法
纯粹的GPS解决方案以及它所生成的经纬度标签是地理位置数据的公认标准.但是至少还有4种方法可以获得地理位置数据: 1.手机信号塔数据:当移动设备的GPS芯片不能接收到GPS信号时,移动设备就需要与它所 ...
- T检验与F检验的区别_f检验和t检验的关系
1,T检验和F检验的由来 一般而言,为了确定从样本(sample)统计结果推论至总体时所犯错的概率,我们会利用统计学家所开发的一些统计方法,进行统计检定. 通过把所得到的统计检定值,与统计学家建立了一 ...
- 手势估计- Hand Pose Estimation
http://blog.csdn.net/myarrow/article/details/51933651 1. 目前进展 1.1 相关资料 1)HANDS CVPR 2016 2 ...
- 通俗理解T检验和F检验
来源: http://blog.sina.com.cn/s/blog_4ee13c2c01016div.html 1,T检验和F检验的由来 一般而言,为了确定从样本(sample)统计结果推论至总 ...
- ML—随机森林·1
Introduction to Random forest(Simplified) With increase in computational power, we can now choose al ...
- 通俗理解T检验与F检验的区别【转】
转自:http://blog.sina.com.cn/s/blog_4ee13c2c01016div.html1,T检验和F检验的由来一般而言,为了确定从样本(sample)统计结果推论至总体时所犯错 ...
- 比较任意两个JSON串是否相等(比较对象是否相等)JAVA版
废话少说,直接入题. 在面向对象语言中,经常会比较两个对象是否相等,而比较的大多是实体类实例,也就是封装数据的那些类实例,或者是Map.List互相嵌套成的复杂数据结构. 比较对象是否相等,常见的思路 ...
- Web指纹识别目的Discuz识别+粗糙的版本演绎
这个识别程序是本学期在我的职业培训项目.它是做一类似至Zoomeye怪东西,然后使用ES集成,为了让搜索引擎寻找.因此,我们必须首先去网上识别相应的能力Web包裹,如果用户输入的关键词:Discuz ...
- 统计学常用概念：T检验、F检验、卡方检验、P值、自由度
1,T检验和F检验的由来 一般而言,为了确定从样本(sample)统计结果推论至总体时所犯错的概率,我们会利用统计学家所开发的一些统计方法,进行统计检定. 通过把所得到的统计检定值,与统计学家建立了一 ...
随机推荐
- JPA error org.hibernate.AnnotationException: No identifier specified for entity
错误:org.hibernate.AnnotationException: No identifier specified for entity 原因:JPA所使用的Entity需要标注@Id,在引用 ...
- lambda（匿名函数）---基于python
在学习python的过程中,lambda的语法时常会使人感到困惑,lambda是什么,为什么要使用lambda,是不是必须使用lambda? 下面就上面的问题进行一下解答. 1.lambda是什么? ...
- ASP.NET MVC5 学习系列之模型绑定
一.理解 Model Binding Model Binding(模型绑定) 是 HTTP 请求和 Action 方法之间的桥梁,它根据 Action 方法中的 Model 类型创建 .NET 对象, ...
- 在服务器中使用 Entity Framework 的 Migration 更新数据库
在开发环境中,每次我们对要对数据库进行更改,比如增加修改表字段等.改好Entity类后,我们只需在Nuget程序包管理控制台运行 update-database 脚本却可: update-databa ...
- nginx 几个常用的标准模块介绍
ngx_http_ssl_module(https) 1:指明是否启用的虚拟主机的ssl功能 ssl on | off; 2:指明虚拟主机使用的证书文件 ssl_certificate /usr/lo ...
- python基础（一）简单入门
一.第一个python程序 1.交互式编程 直接在命令行里面输入python即可进入python交互式命令行,linux下一样: 在 python 提示符中输入以下文本信息,然后按 Enter 键查看 ...
- oracle impdp导入时 提示“ORA-39002: 操作无效 ORA-39070: 无法打开日志文件 ”
第一步:首先使用DBA权限的用户创建directory,我使用system ,可以在服务器本地创建,也可以远程连接sqlplus进行创建,使用的将是服务器上面的路径.要确保创建directory时,操 ...
- 小记IptabLes和IptabLex病毒清理过程
去年有台Linux服务器被黑了,看了500万行日志(现在觉得当时好厉害呀),反正当时的日志文件有700Mb以上大.前两天师兄告诉我,信息中心的老师给他说我们有台服务器应该是被人入侵了,当作内网的跳板, ...
- python编码iso-8859-9编码问题
(2018-10-15) 路 2018骞�10鏈�16鏃�8:30鈥斺€�11:00锛屽湪鍏垽涓€搴叕寮€瀹＄悊锛氬啀瀹＄敵璇�.. (2018-10-15) 路 2018骞�10鏈�16鏃�8: ...
- 洛谷 P1344 [USACO4.4]追查坏牛奶Pollutant Control
题目描述 你第一天接手三鹿牛奶公司就发生了一件倒霉的事情:公司不小心发送了一批有三聚氰胺的牛奶.很不幸,你发现这件事的时候,有三聚氰胺的牛奶已经进入了送货网.这个送货网很大,而且关系复杂.你知道这批牛 ...