Codeforces Round #209 (Div. 2)A贪心 B思路 C思路+快速幂

　　

A. Table

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Simon has a rectangular table consisting of n rows and m columns. Simon numbered the rows of the table from top to bottom starting from one and the columns — from left to right starting from one. We'll represent the cell on the x-th row and the y-th column as a pair of numbers (x, y). The table corners are cells: (1, 1), (n, 1), (1, m), (n, m).

Simon thinks that some cells in this table are good. Besides, it's known that no good cell is the corner of the table.

Initially, all cells of the table are colorless. Simon wants to color all cells of his table. In one move, he can choose any good cell of table (x₁, y₁), an arbitrary corner of the table (x₂, y₂) and color all cells of the table (p, q), which meet both inequations: min(x₁, x₂) ≤ p ≤ max(x₁, x₂), min(y₁, y₂) ≤ q ≤ max(y₁, y₂).

Help Simon! Find the minimum number of operations needed to color all cells of the table. Note that you can color one cell multiple times.

Input

The first line contains exactly two integers n, m (3 ≤ n, m ≤ 50).

Next n lines contain the description of the table cells. Specifically, the i-th line contains m space-separated integers a_i1, a_i2, ..., a_im. If a_ij equals zero, then cell (i, j) isn't good. Otherwise a_ij equals one. It is guaranteed that at least one cell is good. It is guaranteed that no good cell is a corner.

Output

Print a single number — the minimum number of operations Simon needs to carry out his idea.

Examples

Input

3 3
0 0 0
0 1 0
0 0 0

Output

4

Input

4 3
0 0 0
0 0 1
1 0 0
0 0 0

Output

2

Note

In the first sample, the sequence of operations can be like this:

• For the first time you need to choose cell (2, 2) and corner (1, 1).
• For the second time you need to choose cell (2, 2) and corner (3, 3).
• For the third time you need to choose cell (2, 2) and corner (3, 1).
• For the fourth time you need to choose cell (2, 2) and corner (1, 3).

In the second sample the sequence of operations can be like this:

• For the first time you need to choose cell (3, 1) and corner (4, 3).
• For the second time you need to choose cell (2, 3) and corner (1, 1).

题意:n*m的矩阵涂色  每次选取两个点 1个顶点 1个标记为1的点 形成矩形并涂色 问最少要涂几次使得n*m的矩阵全部涂满

题解: 贪心 特判顶点，边界

 #include <iostream>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <algorithm>
 #include <stack>
 #include <queue>
 #include <cmath>
 #include <map>
 #define ll  __int64
 #define mod 1000000007
 #define dazhi 2147483647
 using namespace  std;
 int n,m;
 int mp[][];
 int main()
 {
     scanf("%d %d",&n,&m);
     for(int i=;i<=n;i++)
     {
         for(int j=;j<=m;j++)
         {
             scanf("%d",&mp[i][j]);
         }
     }
     if(mp[][m]==||mp[n][m]==||mp[][]==||mp[n][]==)
     {
         printf("1\n");
         return ;
     }
     for(int i=;i<=n-;i++){
         if(mp[i][]==)
         {
             printf("2\n");
             return ;
         }
     }
       for(int i=;i<=n-;i++){
         if(mp[i][m]==)
         {
             printf("2\n");
             return ;
         }
     }
       for(int i=;i<=m-;i++){
         if(mp[][i]==)
         {
             printf("2\n");
             return ;
         }
     }
       for(int i=;i<=m-;i++){
         if(mp[n][i]==)
         {
             printf("2\n");
             return ;
         }
     }
     printf("4\n");
     return ;
 }

B. Permutation

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

A permutation p is an ordered group of numbers p₁,   p₂,   ...,   p_n, consisting of n distinct positive integers, each is no more than n. We'll define number n as the length of permutation p₁,   p₂,   ...,   p_n.

Simon has a positive integer n and a non-negative integer k, such that 2k ≤ n. Help him find permutation a of length 2n, such that it meets this equation: .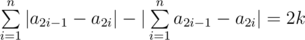

Input

The first line contains two integers n and k (1 ≤ n ≤ 50000, 0 ≤ 2k ≤ n).

Output

Print 2n integers a₁, a₂, ..., a_2n — the required permutation a. It is guaranteed that the solution exists. If there are multiple solutions, you can print any of them.

Examples

Input

1 0

Output

1 2

Input

2 1

Output

3 2 1 4

Input

4 0

Output

2 7 4 6 1 3 5 8

Note

Record |x| represents the absolute value of number x.

In the first sample |1 - 2| - |1 - 2| = 0.

In the second sample |3 - 2| + |1 - 4| - |3 - 2 + 1 - 4| = 1 + 3 - 2 = 2.

In the third sample |2 - 7| + |4 - 6| + |1 - 3| + |5 - 8| - |2 - 7 + 4 - 6 + 1 - 3 + 5 - 8| = 12 - 12 = 0.

题意：构造a数列 使得满足上述的式子

题解：1~2n排列如下

（2n  2n-1） （2n-2 2n-3） ......   （4 3）(2 1)

=>  1 ,1 .....1,1

根据k 的大小 反转k对 输出即可

 #include <iostream>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <algorithm>
 #include <stack>
 #include <queue>
 #include <cmath>
 #include <map>
 #define ll  __int64
 #define mod 1000000007
 #define dazhi 2147483647
 using namespace  std;
 ll n,k;
 struct node
 {
     ll l,r;
     ll w;
 }N[];
 int main()
 {
     scanf("%I64d %I64d",&n,&k);
     ll exm=n*;
     for(int i=;i<=n;i++)
     {
         N[i].l=exm--;
         N[i].r=exm--;
         N[i].w=;
     }
     for(int i=;i<=n;i++)
     {
         if(k==)
           break;
         if(k>=N[i].w)
         {
             k-=N[i].w;
             swap(N[i].l,N[i].r);
         }
     }
     for(int i=;i<=n;i++)
         printf("%I64d %I64d ",N[i].l,N[i].r);
     return ;
 }

C. Prime Number

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Simon has a prime number x and an array of non-negative integers a₁, a₂, ..., a_n.

Simon loves fractions very much. Today he wrote out number on a piece of paper. After Simon led all fractions to a common denominator and summed them up, he got a fraction: , where number t equals x^{a₁ + a₂ + ... + a_n}. Now Simon wants to reduce the resulting fraction.

Help him, find the greatest common divisor of numbers s and t. As GCD can be rather large, print it as a remainder after dividing it by number 1000000007 (10⁹ + 7).

Input

The first line contains two positive integers n and x (1 ≤ n ≤ 10⁵, 2 ≤ x ≤ 10⁹) — the size of the array and the prime number.

The second line contains n space-separated integers a₁, a₂, ..., a_n (0 ≤ a₁ ≤ a₂ ≤ ... ≤ a_n ≤ 10⁹).

Output

Print a single number — the answer to the problem modulo 1000000007 (10⁹ + 7).

Examples

Input

2 2
2 2

Output

8

Input

3 3
1 2 3

Output

27

Input

2 2
29 29

Output

73741817

Input

4 5
0 0 0 0

Output

1

Note

In the first sample . Thus, the answer to the problem is 8.

In the second sample, . The answer to the problem is 27, as 351 = 13·27, 729 = 27·27.

In the third sample the answer to the problem is 1073741824 mod 1000000007 = 73741817.

In the fourth sample . Thus, the answer to the problem is 1.

题意：  通分之后 求分子与分母的gcd  对1e9+7取模

题解：找到分子各项中最小的指数 并标记指数存在的次数 从低指数向上不断进位

注意所求指数应当小于等于分母的指数 之后用到快速幂。

 #include <iostream>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <algorithm>
 #include <stack>
 #include <queue>
 #include <cmath>
 #include <map>
 #define ll  __int64
 #define mod 1000000007
 #define dazhi 2147483647
 using namespace  std;
 ll n,x;
 ll a[];
 ll b[];
 map<ll,ll>mp;
 ll sum;
 ll gcd(ll a,ll b){return b==?a:gcd(b,a%b);}
 ll quickmod(ll aa,ll bb)
 {
     ll re=;
     while(bb)
     {
         if(bb&)
             re=(re*aa)%mod;
         aa=(aa*aa)%mod;
         bb=bb>>;
     }
     return re%mod;
 }
 int main()
 {
     sum=;
     int jishu=;
     mp.clear();
     scanf("%I64d %I64d",&n,&x);
     for(ll i=;i<=n;i++)
     {
         scanf("%I64d",&a[i]);
         sum+=a[i];
     }
     for(ll i=;i<=n;i++)
     {
         ll exm=sum-a[i];
         if(mp[exm]==)
         {
             b[jishu++]=exm;
         }
         mp[exm]++;
     }
     sort(b,b+jishu);
     ll ans=b[];
     while()
     {
         if(mp[ans]%x==){
             mp[ans+]+=(mp[ans]/x);
             ans++;
         }
         else
             break;
     }
     if(ans>sum)
       ans=sum;
     printf("%I64d\n",(quickmod(x,ans)%mod));
     return ;
 }