[Math]PHI, the golden ratio
PHI, the golden ratio 黄金分割比
转载自 http://paulbourke.net/miscellaneous/miscnumbers/
1. Definition
将一个线段分成两段,那么长的部分与短的那部分的比率等于整个线段与长的部分的比率时,

这个条件可被解释为 $\frac{a}{1-a}=\frac{1}{a}$.即如下的二项式: $a^2+a-1=0$,方程有两个解, $-\phi$,和$\phi-1$。
$$\therefore \phi = \frac{\sqrt{5}+1}{2} \approx 1.618$$
这是古希腊数学中初始定义,我们一般用$\phi-1$
$$\phi-1 = \frac{\sqrt{5}-1}{2} \approx 0.618$$
2. 常见关系式
\begin{align*}
& \phi^2=1+\phi \qquad \phi^3 = 1+2\phi\\
& \frac{1}{\phi}=\phi-1 \qquad \frac{1}{\phi^2} = 2-\phi\\
& \sin(18)=\frac{\phi-1}{2} \qquad \cos(36)=\frac{\phi}{2}\\
& \phi^{x+1}=\phi^{x}+\phi^{x-1}
\end{align*}
3. Continued_fraction 连分式
关于一些常见连分式,参见Wiki之Continued_fraction .

phi = sqrt(1 + sqrt(1 + sqrt(1 + sqrt(1 + .....))))
4. Relationship to the Fibonnaci series
(1).Ratio
当斐波那契数列趋向$\infty$时,$a_{n-1}/a_{n}$趋近于$\phi-1$
\begin{align*}
&1\quad 1\quad 2\quad 3\quad 5\quad 8\quad 13\quad 21\quad 34\quad 55\quad 89\cdots\\
&1\quad 0.5 \quad 0.67 \quad 0.6\quad 0.625 \quad 0.6154 \quad 0.619 \quad 0.6176\quad 0.6182\cdots
\end{align*}
(2).Phi Fibonnaci series
数列满足下面两个条件:
\begin{align*}
&(a).u_{n+1}=u_{n}+u_{n-1}\\
&(b).\frac{u_{n+1}}{u_{n}}=constant\\
\end{align*}
验证可知,这样的数列有且仅有一个:
$$1,phi,1+phi,2+3phi,3+5phi,5+6phi,\cdots$$
5. 2 dimensional golden ratio 二维黄金分割比
由原来的一维线段归纳推导出来的定义为: "find a rectangle such that when a square is removed the remaining rectangle has the same proportions as the original". The solution to this is a rectangle with the ratio of its sides being phi.
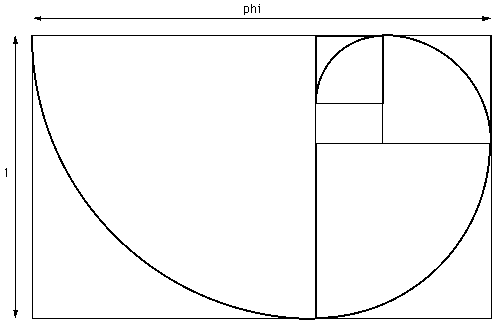
These rectangles can be inscribed in a so called logarithmic(对数的) spiral(螺旋) also known as equiangular(等角) spirals. Such spirals and occur frequently in nature, for example: shells(贝壳), sunflowers, and pine cones(松果). The limit point of the spiral is called the "eye of God".
6.Phi Pyramid
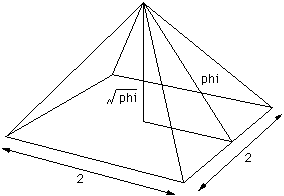
[Math]PHI, the golden ratio的更多相关文章
- The golden ratio: 1.618
http://www.chinaz.com/design/2015/1109/467968_2.shtml The golden ratio: 1.618 a/b=b/(a+b) The Fibona ...
- ACM学习历程——HDU4814 Golden Radio Base(数学递推) (12年成都区域赛)
Description Golden ratio base (GRB) is a non-integer positional numeral system that uses the golden ...
- Applying Eigenvalues to the Fibonacci Problem
http://scottsievert.github.io/blog/2015/01/31/the-mysterious-eigenvalue/ The Fibonacci problem is a ...
- Perl包和模块(内容来自beginning perl)
单文件版的perl程序只能用于构建较小的脚本程序.当代码规模较大时,应该遵循下面两条规则来构建程序.这样能将程序的各个部分按功能一个一个地细化,便于维护,也便于后续开发. 能复用的代码放进函数 能复用 ...
- python turtle 例子 海归绘图
太阳花 1 # coding=utf-8 2 import turtle 3 import time 4 5 # 同时设置pencolor="red", fillc ...
- ThreadLocal源码分析
1.概述 ThreadLocal,可以理解为线程的局部变量,作用就是为每一个使用该变量的线程都提供一个变量值的副本,每一个线程都可以独立地改变自己的副本,而不会和其它线程的副本冲突. ThreadLo ...
- Think Python - Chapter 03 - Functions
3.1 Function callsIn the context of programming, a function is a named sequence of statements that p ...
- hdu 1527 取石子游戏(Wythoff Game)
题意:Wythoff Game 思路:Wythoff Game #include<iostream> #include<stdio.h> #include<math.h& ...
- <转>机器学习笔记之奇异值分解的几何解释与简单应用
看到的一篇比较好的关于SVD几何解释与简单应用的文章,其实是有中文译本的,但是翻译的太烂,还不如直接看英文原文的.课本上学的往往是知其然不知其所以然,希望这篇文能为所有初学svd的童鞋提供些直观的认识 ...
随机推荐
- Response attachment filename 中文乱码
Response.setHeader("Content-Disposition", "attachment; filename=" + fileName+&qu ...
- 解决node-sass安装不了的问题
1.下载https://github.com/sass/node-sass-binaries/blob/master/win32-x64-48_binding.node到E:\primeng\lib目 ...
- 解题报告:hdu2602 Bone collector 01背包模板
2017-09-03 15:42:20 writer:pprp 01背包裸题,直接用一维阵列的做法就可以了 /* @theme: 01 背包问题 - 一维阵列 hdu 2602 @writer:ppr ...
- Python基础笔记系列十一:标准输入输出、文件读写和指针等操作
本系列教程供个人学习笔记使用,如果您要浏览可能需要其它编程语言基础(如C语言),why?因为我写得烂啊,只有我自己看得懂!! 标准输入输出一.输入 在sublime中这个时候需要安装SublimeRE ...
- nodejs 备忘
引入模块(在于你用什么模块,需要的模块可以用终端进行安装, npm,一般express,swig,body-parser,cookies,markdown) 设置模块 设置渲染 var express ...
- gitlab 去除代码保护
- Nordic老版官网介绍(2018-11-30停止更新)
1. Nordic官网及资料下载 Nordic官网主页:https://www.nordicsemi.com/,进入官网后,一般点击“Products”标签页,即进入Nordic产品下载首页,其独立链 ...
- 【三小时学会Kubernetes!(零) 】系统结构及相关示例微服务介绍
写在前面 牢牢占据容器技术统治地位的 Kubernetes,其重要性想必不言而喻,我保证本文是最详尽的 Kubernetes 技术文档,从我在后台排版了这么漫长的时间就能看出来.废话不多说 — — 以 ...
- CSS 左边div固定,右边div自适应
有时候我们会有这样的需求,如图,aside是导航或者某些链接,右边的main是显示重要的内容,左边需要定宽,右边的main能够自适应剩余的宽度: <!DOCTYPE html PUBLIC &q ...
- C#多线程3种创建Thread、Delegate.BeginInvoke、线程池
1 创建多线程,一般情况有以下几种:(1)通过Thread类 (2)通过Delegate.BeginInvoke方法 (3)线程池 using System; using System.C ...
