CRC32为例详细解析（菜鸟至老鸟进阶）

CRC-知识解析 cyclic redundancy check

写在前面的话：

之前在做学校项目的时候用到了CRC 原理，但在网上查找的过程中，发现讲解CRC知识的资源很多，但是对新手比较友好的、讲的十分清楚的又很少，很多博主也不求甚解，弄得读起来心中常常不由自主地奔腾过上千个“为什么”“为什么”， 本文是我在阅读了许多资料的基础上整理、解析出来的文章，尽可能的对新手友好、解答CRC里面的一些知识点，而不是简单的应用。

依据学习目的不同，如果大家只想简单应用，不求原理，那么直接复制--粘贴最后的代码即可。

-----------------------------------------------------------------------这是一条华丽的分界线-----------------------------------------------------------------------------------------

1. CRC 算法原理

在对信息的处理过程中，我们可以将要被处理的数据块M看成一个n阶的二进制多项式，其形式如下：

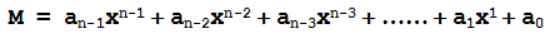
CRC校验就是基于这种多项式进行的运算，以GF(2)(The integers modulo 2)多项式算术为数学基础，即(模-2)除法的余数运算（其实说白了就是异或Xor（见2.2）），使用的除数不同，CRC的类型也就不一样。CRC传输实际上就是在长度为 k 的数据后面添加供差错检测(Frame Check Sequence) 用的 r 位冗余码（Redundant code 没错CRC里面的R就是这个），使原数据构成 n = k + r 位并发送出去, 此方式又叫（n, k）码。可以证明存在一个最高次幂为n-k=r的多项式G(x),  根据G(x)可以生成k位信息的校验码，而 G(x) 叫做这个CRC码的生成多项式( Poly )。而根据 k 值的不同，就形成了不同的CRC码的生成多项式，以下为各种常用的多项表达式：

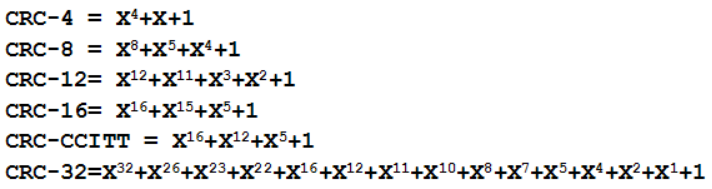
这些多项表达式的值便是(模-2)除法的除数，本博客这里选取CRC-32多项式（即为对应除数）格式，通过取余做操，获取CRC检验码。

2. CRC 传输过程

2.1 传输原理

aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAesAAAFSCAIAAABdVGBLAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAE/mlUWHRYTUw6Y29tLmFkb2JlLnhtcAAAAAAAPD94cGFja2V0IGJlZ2luPSLvu78iIGlkPSJXNU0wTXBDZWhpSHpyZVN6TlRjemtjOWQiPz4gPHg6eG1wbWV0YSB4bWxuczp4PSJhZG9iZTpuczptZXRhLyIgeDp4bXB0az0iQWRvYmUgWE1QIENvcmUgNS42LWMxNDIgNzkuMTYwOTI0LCAyMDE3LzA3LzEzLTAxOjA2OjM5ICAgICAgICAiPiA8cmRmOlJERiB4bWxuczpyZGY9Imh0dHA6Ly93d3cudzMub3JnLzE5OTkvMDIvMjItcmRmLXN5bnRheC1ucyMiPiA8cmRmOkRlc2NyaXB0aW9uIHJkZjphYm91dD0iIiB4bWxuczp4bXA9Imh0dHA6Ly9ucy5hZG9iZS5jb20veGFwLzEuMC8iIHhtbG5zOmRjPSJodHRwOi8vcHVybC5vcmcvZGMvZWxlbWVudHMvMS4xLyIgeG1sbnM6cGhvdG9zaG9wPSJodHRwOi8vbnMuYWRvYmUuY29tL3Bob3Rvc2hvcC8xLjAvIiB4bWxuczp4bXBNTT0iaHR0cDovL25zLmFkb2JlLmNvbS94YXAvMS4wL21tLyIgeG1sbnM6c3RFdnQ9Imh0dHA6Ly9ucy5hZG9iZS5jb20veGFwLzEuMC9zVHlwZS9SZXNvdXJjZUV2ZW50IyIgeG1wOkNyZWF0b3JUb29sPSJBZG9iZSBQaG90b3Nob3AgQ0MgKFdpbmRvd3MpIiB4bXA6Q3JlYXRlRGF0ZT0iMjAxOS0wMS0xM1QwMDowOTo1N1oiIHhtcDpNb2RpZnlEYXRlPSIyMDE5LTAxLTEzVDAwOjEyOjQxWiIgeG1wOk1ldGFkYXRhRGF0ZT0iMjAxOS0wMS0xM1QwMDoxMjo0MVoiIGRjOmZvcm1hdD0iaW1hZ2UvcG5nIiBwaG90b3Nob3A6Q29sb3JNb2RlPSIzIiBwaG90b3Nob3A6SUNDUHJvZmlsZT0ic1JHQiBJRUM2MTk2Ni0yLjEiIHhtcE1NOkluc3RhbmNlSUQ9InhtcC5paWQ6MTliYzBjYWMtYWVjNy1hZDQwLTg3ZDMtNjVhOGViNWYwYjAzIiB4bXBNTTpEb2N1bWVudElEPSJ4bXAuZGlkOjE5YmMwY2FjLWFlYzctYWQ0MC04N2QzLTY1YThlYjVmMGIwMyIgeG1wTU06T3JpZ2luYWxEb2N1bWVudElEPSJ4bXAuZGlkOjE5YmMwY2FjLWFlYzctYWQ0MC04N2QzLTY1YThlYjVmMGIwMyI+IDx4bXBNTTpIaXN0b3J5PiA8cmRmOlNlcT4gPHJkZjpsaSBzdEV2dDphY3Rpb249ImNyZWF0ZWQiIHN0RXZ0Omluc3RhbmNlSUQ9InhtcC5paWQ6MTliYzBjYWMtYWVjNy1hZDQwLTg3ZDMtNjVhOGViNWYwYjAzIiBzdEV2dDp3aGVuPSIyMDE5LTAxLTEzVDAwOjA5OjU3WiIgc3RFdnQ6c29mdHdhcmVBZ2VudD0iQWRvYmUgUGhvdG9zaG9wIENDIChXaW5kb3dzKSIvPiA8L3JkZjpTZXE+IDwveG1wTU06SGlzdG9yeT4gPC9yZGY6RGVzY3JpcHRpb24+IDwvcmRmOlJERj4gPC94OnhtcG1ldGE+IDw/eHBhY2tldCBlbmQ9InIiPz56KZHSAAAuFUlEQVR4nO3dfWwbZ54f8B9fxMgySe1y87KyTedILmV1y6qHS4X8dadIqySXFaTEUiCgfxSGAbmKGxjpyqilKwwcCuhwYQIrNYLAEWJANa5oATWSG2mNzYtMxcAFV53q7a5O29piKK6XkpVsYiYSaZqiSE7/mBcOyRlySFEkR/x+YCDMzMOHQ0r68plnfjOjYRiGAABAhbSV3gAAACgSEhwAQK2Q4AAAaoUEBwBQKyQ4AIBaIcEBANQKCQ4AoFZIcAAAtUKCAwCoFRIcAECtkOAAAGqFBAcAUCskOACAWiHBAQDUCgkOAKBWSHAAALVCggMAqBUSHABArZDgAABqhQQHAFArJDgAgFohwQEA1AoJDlCr5keCVmfQ6gx2X01UelugOPpKbwAcMOsffH72zW0iIlfLlY+ajxXZLPThywvXVkQL+tvm3mrK6kZhMxVsWyXYnXqieKW3AvZCwzBMpbcBDg7/6htdd9bYxzlSMnczz+2eMxtSTzt60ffMs4U2U8W27bv5keDpmUKfZJj0GrvECzxh61BMvGBgwnKpc6/bBnuAWRQoGXH2Fd9sc1w6+4hoY+zCZoHN1LBtauCPdjuDGfFNRFNDQaszPF+RTQIiJDiUyOKF2R4FEZm/mef+gvC4v23O1zvna+sQlkzfXyyoWdVvW7l0uS0BL/vPOMAtM0x6hYWWWyPcjOrARKolNwD3R7tfiCzL9h07jRCvGCQ47NnmuGN2bLo0zRY/Fkav5lNn2VnjpoFRM79w4wtPAc2qe9sK4492l+aQo+F1Lqxj7wi9+aPn3HEiIlfD65mzIomJ4VR8t440Zoc+Uez0SObwHMoCCQ4lZB9t6cjfSmEzk9XGPTrmMAlL7/lCRTWr6m3LzRO2OoPWXKNgJWLnnVzlSbubO3q57N5il6Q6X4m0883Os180/t1Z/nDswITlxqBO6NE+aA5MGLj/mYlO+Pe0fVAUJDiUhH20Y87Xe/mMaW/NQoG7UottJnsxzVSwbTmtXd22pmafDZPetAAtj7WbMS7cJYbnRJ0Gfk4mvooErwBUE8KeNQ37ekvXrLSqedtySC8dyaoJ2YPWkUb2a2Dt6vY5Osw+nh8Jnp7hXyV91nvNy5cbNmulvoN0zS6iFSKiO2sJ6iz3F0zNwxgcqonJekJqsT+0Vkyz0irbtqXi29VwS3xEMU1i4iQ33ZE26SG7PPMl2t3xZffDCT8RJYj0RLHTzqB1D9PZLXbEd/khwaGqHHUKR/xCAX63fF00cfy0w6S8We1sWwF2zzu5b4jWkcNDNiLSdbnNk31ERDQTzphwtzv5/fTVpNR3UGJ1RWIplAsSHKqK6Ijf9rUrbOn05hR7hiQRkfm4rYBm6ty2LreFy1PuuKJkrZ5u6HqqFjDgFc6skVvOWXZHplKPt4Shutz5PnY7nxErkfeyh/OeGN+b4SWc2lMBSHCoLp1HRKXTSz2O2R7Hkqi8+sSrtkKaqXXb2PJtvlwvdlo2xwvWOtIw4GqYHJE8AmaYnDC09hlaxcs6D110cQ+nhtLmZNaubgvn+LSOHCrVTD0UAgkOVaZpeL5FpmxDKK9W3qy0yrxt9kFzwGvhK/Zip0tTD1536Xo9t3V9Rm6oLhQFdhpvvJYR7rqh8QYh06eGUjPsQlUiuRreLXuRDBAREhyqkK35sq/jlCt9YX/bnO+5tNGrwmbq37ZOY8BrCXza0Jq/aYFmwlwcZ50un8ZWf0OI+GyuhlvCVwKUG65sBVATYued4Sm+mnDt6nZqBJ1imPQau/hqwuyrVmVdHquUZY5QFIzBAWqWMIsiuhBK6hSeLMLFVbgDrRQ7fTK6nwWckBcSHKD2cDPs7tTciHC3B35snqu2pMvNXx5rJdKOy1pVEhIcAMR130QKpkcMl1Lz8mypDO71UxGYBweA4mRddVY4ZR/KBWNwACiOrf6Gt/GiK39D2DcYgwMAqBXG4AAAaoUEBwBQKyQ4AIBaIcEBANQK9+g5CBITJ7fGxJdp7mu4uBrBEvUsMYpPrgFQDGNwAAC1QoIDAKgV6sEBANQKY3AAALVCggMAqFVxCe6PdjuDVmfaTfOyJCZOSl2ujH8uLmMGALA3cgnuCQt3w+P+jaTuwzT/PndBsql3Ja7vPj+Snc6JiZN83Pvjy0RE+t6f4RpmAAB7UcQY3BNO3WlpJXIuI6w94dMztOzeEg/P50e2xlZoaig8TzT/SYyIyGV4Puf9AoXrzYv+4ULyAPvGE7Y6tyf8EmvWrm5bnUFrobfjwZ56OeQ+o8fVcOt63Wcnt8ZWqNXJDplj54dixF4I2P7IOhRbdm+dt4vup9dpvDWy3e7WNtuEj36XyECUvPipsYti59n0X4m0OyPC64jvyJd1Lz5B7PRIrAInPqx/8PnZN7eJiFwtVz5qPpa5PvThywvXxKdn9LfNvSV7P/J8vRXWjFLXaM6+q+F+vWiJPpCKfG6l3bZ9eacV4QmzNzseG44+r/y2xfyzUkSnJon31F/vzOxzfiT4jrPxxqB4WWLi5NbqOculTuypK5d/DJ5YXSEiarHrhJulkqvh3UEddRrZ2+VNDaW+ZudH2Ls0xcZeCLNnnS27I6dnYkTxsfdj5IlN5XytiZNy8V0p/tW32USQ5Lnd40j/4ySi6aUex+3FInortBkREdnqel1EMjNa+/CiJflAKvK5lXbb9umdVkin8daInkjYq46dF+3+cvddW4m0K98h3rc9dW6HgPsnvdOQtgcv2nXgn3uQ9ubzJjiXuYaXOvn4JsMk/y3d5eau7z41pGh/h/vB8PdXZb8AWkca2cHj2tWHolONDZNp92C1BCb2OvqeHyn0h+dffaPrjvyu4+b4mQ2ZVRtjFzYL7K3AZgLd893iv719fdHSfCAV+dxKu237804ryT5YP1DcTXZcDbf4+zxk76mzf7YZYc1/YRiy9tT17J76r1J76qkslpqNic/ezP6d558uu8F6pTsZKpAvwdfWkkREFDvNxTeJb4tndaYux7Hsfjjh5+5mzX2fExH7U2Qj2E3cJ7uaXCMiSvhWxS8Ve4+7xSob8Vm36essybUj2I2X/upOs3hhtid3cHjuLwiP+9vmfL1zvrYOYcn0ffEgK39vhTRLZ/+Zgb1j4bL7Udr3U2lftGQfSEU+t9Ju2z6808rhR6zhKaJl95Z40DowIfpzdjXckh1IlXNPPc3yjd3MH7v80+32g1c9necdxX91I05ErSONt0b05DIMSN5RydVwa8JAffVDNmL3v9qFLGZ/J5zB7quJtatR7pNdibMJLvqpiz93w+T+THZ3uS0B7vas8bEXch1j2Rx3zI5N5+lu8WNheGU+dZad1mwaGDXzCze+8BTQm+JmEviJFKLYr/h3VNoXLeUHUpHPrbTbVup3ulf+aHe5DvpxQ7qMYWwZ99R5+lb2d34l8p5H6ukufSvJaNbWzhg8eWeF2OMJ9kFz4Lrx0nVLwCvkIPcVHbheb+cGyMLPT3/x07Qb6C27t0SxnvT5ifzJO0RE+mYbUWqwn/bLkV2RkvO4tgK2+hui7Z8ayne82z7a0iG7UmCy8tN1xxwmYek9X6io3pQ2S9E5mrlHU5/EMleW9kVL+oFU5HMr7baV+J0Wiq36Tb/dcKHY/Wbhj6K1uy5/wKWHYBn31FN6u7lxXtrvvD/6zgz7Lgwt2c/pNAa8loN1GcjcCb6i7R3RE8XHhhUWEhleH9FTnzHgrV99gfuxtY40BryNF1000Gfgvznjq37hcLPWkbOsUAZXhJSV7HLL07E57jUOEBHRsntLIsTtox1zvt7LZ0xZz2aFAncluzZJ/vrn662wZtnPc/J/DNzv/T68aIk+kIp8bqXdtn15pwXiDspxpSCGSa9ljzeJ50tHDL/I2Y990JwVgmXcUxf7mYH9+6WZmDB5uHYzxhWx2OlO3vd8EOSpJtQ/P6hddYenVmKfeWh2KPOrfmoomJpy6jMG3Ab7oDlARP4o+/EJJW5D1y1E9NKLMftatH0lPvVJ7CVi95UM7Hx3aopqJb5GVNndnKZhX2/Ze9vLi2Z/eqV90dJ+IApV87ZVUHq5rWEy+4hREYSh68gh+9Xt8/Z6dnHaH7i4AjjtguaiPXWbOTBIRHSJpOtcA52Uvqd+mIbFI/St9tQ2JX1+6qK0PfV0hpf6aGqG2MnDrk4iSnx2I07EFbHM7uHzUI/8M/u6ZhcRxWc/iedtmhoC87t17DSFMBzu6jRwh91muGKjgRf53wObMG8Ve4cfEXP7d/xcmHirhq6nVarwvyJyy9Nx5wtwe3zFHH8nMllPSHYdKvA4ZKklfXkP0u4PhR9IRT630m5bBd9pKr7Z44rS8V3oHmpiYjjC118n3nPHp4bCyo8lVnBPves1fjqULaX1786uEBENnFNc0q56ChKcm2N1HrohJGPGPDg3gaVsdsmmFc1PGV4SEjZ1OC7zgHgpsdnNf8Gw21/k7udRp3BIKhTgU3NdNLP5tKPQyRB1U/iBVORzK+22VfM7LRxbiM2aHQ5PEbWONLATFAMTllsj+tQktTBX7hT9ybj0zw/WDxDRSuwzD3cupdwwjr04h33QHHAb+CNhNDDB/g3qhq5bLrmNkxP173briWjqkxh/VNMgvZ8hhMZK7DN/aiLoJclx28Gk4Iye1JEET1iintof7U4V5+mGrvPjZW6MIByvED5Ww+v8EYzWkUOiH4xuaLwhdfg4vRS0JKf5zI8Iv1X6i5/Kj9AVEh2S2r52ha3t3ZxKnVFiPl7MBP+eFXdcoRQUfiAV+dxKu22Ve6ddbv7vi/sDkTy/oaA9VHH1dHx5ha0C5HLhzrvb7e64UKWammXOPFWyXHvq2e/0HLsqPnszyr0Rubg/mHLPg69E2p3cwxZ7gq3SP30yemtcaBE7/0JkmWhZOBlXOBdrJdLujE9O0Gk3e5SDD2t/9Bx/BGPZ/Wh+ULQbaKu/4dWedxayB1ewEs0bEhF1HumgDa7gd3qpJ6Ogrf/Eq+WLUslKnrJT+IFU5HMr7bZV8p12uS0BN61d3WZLqk87g3v7rRZmk4lI3+qKL69Ezl1tYHeUW87VtwyFp9gLWryW5P5yuaORYjpHM9EKu6du5JbJXu9BQdWjTdtCxB91yzmm7jQMUGyKaPkGe1BXf/G1g1RqklfuMTh/WLl1xNj8Lhes6XNMhkvsjpVwQiBbr8OV/cdOD3GlndxMBf9D5cVOZ86WGC6JdtbS9Bn3OGrucsvNGxapaXi+RSYvhfrf8ljz8mOfita6KvxAKvK5lXbbKv5OuZoQ4Q9tD/XgdmfDJF+X1TtumeyjZXeEPdLYbOP3mGfC/JBZ8nSNsu2pZzO8xO2UxJcp/yXzDpw8syj6169bAl7LL7zcqVPkang9dd0ZIiKy1f+ij4iv9CSSut7NTDhjaoydXyMiWom0j2SVMHPVfun/qrGK09Z82ddxKqN4qr9tzvdcGQfg4r8f+f3N8lD4gVTkcyvttlXHO2UHTJIjHsXsg/XiiOxyp514aR88LD6xY2Aiawy0EmnnK775PfWMkRm7py461Jm2px6e94Tbc++p59x+4XgmKSxmP1gYaTdDx37y4Ngrj3ziJa888rHLuX9b76+x63aGf7L1/lrct7YznFr74NiFHX7tg59/sPP+K9zyn38QZ5/22QVuyfBNmc0AJdYe/Zz7zEOfVXpbDgThd7jSG1I+7F8u9xfN/2GGPmP4KMj8o2YYYdUroeFX2L/r1N/48M3Ur6X4sfC3z+ToOfX7zP8TBZHvg6308GEYJs6/ruj3X+hEHGIHkNydjtlxtKvhVualJmOpeeo+qQuVeMLWoZhMfV7svDPa/KlZNImWmDj5kMbNWdNqUAh+p6e4ssiDImjljtlYAt7iGuxfS+UdVgr7d62/+Kl5yCZc2ETfuiLa2xYIsZCeEmmVjtfr7fyvJTsPzq9lX0JqTz3LwITl9bVt7sQfybQB2SOZnUaZXzXDJa/lUo4OZZ/IPjfjZ6Abum6WbgtKJSbeZS8E0fCuyuL7wMTfgSKcFTnQrJ3iqgzZ2E1MnNwaW2GnPmIXPzUPpT+xy20JvBi2vqu/dS7e7gzyi7mTcbrcxoGZaPOnh58XjwJJiObYeWf4zoix90ZYqBC/1EnUaZ70Bk/PEM2Ez7+4t+Kxgyl3LQpUP+4sBv3F8do5iwH2kX3QHPhZtHuYXnfXv+7cbvfW84Nf3dB1y5A/2v1CrJcdR2efO9ZpZM+6ZOtDiMSFK8IATndpwjCVuaduuOS1EBENGlfT99S73I0XV7GnLkduFgVg35V2DI5ZFKhBB+96uQAAtQIJDgCgVkhwAAC1QoIDAKgVEhwAQK2Q4AAAaoUEBwBQKyQ4AIBa4ZzMGrH+wedn2XsLuFqufNR8LHN96MOXF66tiBb0t829JXv503y9FdYMAIqEMXhN8K++nbo1TBbP7R5HenwT0fRSj+P2YhG9FdoMAIqGBD/4/KtvdN2Rv+vo5viZDZlVG2MXNgvsrcBmALAXSPCDbfHCbE/uJPXcXxAe97fN+XrnfG0dwpLp++JheP7eCmkGAHuFefCDa3PcsbSQr9Hix8IAXLjvV9PAqHmBmwDZ+MLzzLOdSntT3AwASgFj8FpgH23pyN/KZOUv3ym6yTrd84WK6k1pMwAoHhL8YLOPdsz5ei+fMcmsDwXuSi22mSSvNZ6vt8KaAcBeYRbl4Goa9vWWvbfSvigA5IQxeG0zWU9ILfaHcBwSQAWQ4DXuqFO4UWkowN81a1009/20A5MhANUKCV7jRActt69dYau/N6dSZ+KYj+PuhABVC/Pgta7zSAdtcPV/00s90+lr+0+8igQHqFoYg9e8puH5Fpm73AsV4gBQlZDgQLbmy76OU670hf1tc77nMAAHqGoahmEqvQ1Qo4JWJ/vAEvCWoZnCfvajpfIOAQqCMTgAgFohwQEA1AoJDgCgVkhwAAC1QoIDAKgVEhwAQK2Q4AAAaoWz6g+gxMTJrTHxjYv7Gi6uRqpgCaqhAUoLY3AAALVCggMAqBXOqoeKwVn1AHuEMTgAgFohwQEA1AoJDgCgVkhwAAC1QoIDAKgVEhwAQK2Q4AAAaoWz6qFiUBwNsEcYgwMAqBXG4EBE6x98fvbNbSIiV8uVj5qPZa4PffjywjXx1ar62+beaipPbwAgC2NwIP/q22zgSvLc7nGkBy4RTS/1OG4vlqE3AMgBCV7r/KtvdN1Zk129OX5mQ2bVxtiFzf3tDQByQ4LXssULsz25ApfIc39BeNzfNufrnfO1dQhLpu+LB86l7Q0A8kOC16rNccfs2HSeRosfC0Nm86mz7FR108ComV+48YVnP3oDAGWQ4GAfbenI38pktXGPjjlMwtJ7vtC+9gYAuSDBa5l9tGPO13v5jElmfShwV2qxzWTf/94AID9UE9aqpmFfb7X2BgDKYAwO8kzWE1KL/aFchyvL1BsAIMEhp6NO4TBjKODnHq2LZqufdsjNmex7bwCABIdcRIcZt69dYeu1N6dSJ+yYj9sknlWe3gAA8+CQU+eRDtrgirinl3oy6gX7T7xaUOaWtjcAwBgccmoanm+RqRURaror1RtAzUOCQx625su+jlOu9IX9bXO+54oZMpe2N4Aap2EYptLbAJBL0OpkH+S+nnjeZgr72Y+WyjsEKAjG4AAAaoUEBwBQKyQ4AIBaIcEBANQKCQ4AoFZIcAAAtUKCAwCoFRIcAECtkOAAAGqFBAcAUCskOACAWiHBAQDUCtcHByJa/+Dzs+ydFlwtVz5qPpa5PvThywvXVkQL+tvm3pK9GGy+3gprBgCyMAYH8q++nbpRThbP7R5HenwT0fRSj+P2YhG9FdoMAHJAgtc6/+obXXfk7zW8OX5mQ2bVxtiFzQJ7K7AZAOSGBK9lixdme3Inqef+gvC4v23O1zvna+sQlkzfFw/D8/dWSDMAyA/z4LVqc9yxtJCv0eLHwgBcuAta08CoeYGbANn4wvPMs51Ke1PcDACUwRgc7KMtHflbmaz8XdBEt5yne75QUb0pbQYAuSDBa5l9tGPO13v5jElmfShwV2qxzSR5t+J8vRXWDADywyxKrWoa9vWWvbfSvihAzcMYHOSZrCekFvtDOA4JUBWQ4JDDUaeZfxgK+LlH66K576cdmAwBqBwkOOQgOmi5fe0KW/29OZU6E8d83CbxLAAoE8yDQy6dRzpog6v/m17qmU5f23/iVSQ4QAVhDA45NQ3Pt0hWnogqxAGgQpDgkIet+bKv45QrfWF/25zvOQzAASpMwzBMpbcBIJeg1ck+sAS8e2mmsJ/9aKm8Q4CCYAwOAKBWSHAAALVCggMAqBUSHABArZDgAABqhQQHAFArJDgAgFohweFg0WiKWQWgTrguSi1KJpPM1L/b+qtblEgQd0pXX8PF1ciY+Jb0lVmyx3NeNAZDjlXMzs5eOgeoNkjwWhSL7ehMRzSHG5jII0okKJlMrdPpSKMhrVajrSO9QXPoEGk0DMMQw1BSTxod6XTE/m8Vns2r1WosP5RbqfmRhfnq67Q3C6BySPBaVFdn0Bx16f7sXuK7rWhDXf3KXSaqJ61O09io+eEPtJYfahrNdPif6exPGvqcybq6naceT8TjDb8xa59K6hwRCj9MRiIUizG7OtJoSatNBbpORzod1dcTETFJSiSI0RKVa/pCr9ceOyq3Unv0SPLbBxSLlWljssnvHwAUBwlei3Q6Hf1pn/G/vLyzE9Xtxs3mRnZ5/ZnMlvrnGCI6zCSJSKvVEZHh5cw29f82a8lg1pKhYpYUSqPXaR9/XG6t9onHNXV6Znd3ry9THI1G+/iPKvPScHAhwWuXVqs7dOhwfX2uyRCNRkNEGo2uXBu1NxqNpv4x2ZWP1ZNGozlUX84tStHrdM6fJJMJ9osQoCRQi1LrNAeoQoNJMoxW9lea0RBDGu2RfbiouYLPUPNYvc710/JNKEFtQIJD1WNDWT6aOXqdpk6vPXxYbr1Gp9Meqtc1N+d/RTaR874iEel0RKQ5dChvw4TlBzvPPnOQvi+hGiDBoXwSifjubgEHEuPx3a2t4Dd/+Vz0yFMao2w07+7uMgyjeewxzaFD2mNHZHszHv7q5Re3X3kp7zXxNUYjabVUl2uOMZlMPnr0kOrqSKfTHs0zrg832yJOO+kxaQklhgSH8tHp9Hp9nfL2en1dY6Plh2t/uH/yLzUOmZu9EdXV1SWTCc3hw5of/Ujb7JQLaO3m142//Z3WaJJcm/a6f/ovNIcPU12u0hGtVhuLxZgfP0F6vfZPns7doXHVb779W+1XX+OGKlBaSHAoqyKmETQ6vWEnpm115W5FdQbtkR+T8ydyL8F88w3F4szuTt5tqHu+S9v0Y3aGJAeD4bHEk0+SXq/98VMMk6fMPLm7u7uJBIcSQ4JDtav79oF15pO6plwzFTqdjmGS2ief1DSa5dokH3yX3InGv9vK+4r6n7Zojx/T5Jv00Gq1yUOHiGGoTp8/mXfj8QffJpPxvK8OoBwSHKpd8uEj0mo0dbLTL+zAVrMT0zxmyHX48dEjJra7+92D/C95+LCm4TAlErlbabVandlEWq0mqcm/b8EwzMNIIoEzQqGUkOBQ9aJRiu0mv/6j5EqGYYLBb3Z2osxONBl+yOxEJdsQEfMoQslkLBjM/4q7MeZhmOJ5zv3R6fR6u40MBo3ZmKdDjYaYZOJhOJHvWwGgIDg4DhXAMEwkEm5oMCqaFo/HmZ2d7UioQWqlRqNJJpPffx986v/9hoh2dqIMw4i7ZRgmmUzodPof/u7Xuu3vH329kfcFE1+uJQMbzE6eshmNRmNoORF/4gnNE4/nfyOJJH2/jQSH0kKCQ5kl/uHLyf/2+/U/if/omyf/4s0/+5eSjWKxR3c254e/vPGHyOZPby5cMTEWyxPsqvSAjvzyN2NzX2vu7K5bmv/mevMxvb4uGn106FAD3zgZDAen1z1/t/7x19EHRzWWf3P0vDPn9sXju7sLt5L3N/POomg0Gp3Fkmg4lL8enGGI6LHNr2IxXBwRSgkJDuXDMEwkvPLOV6vJ3Z1jmh881MlObX//4Jcz9zb++e6Pj+saj4b+aD7a/Nhj3NnwiUT8+++DGo1Wp9N++9WHU1/tfhcPryeDPyAiIp1Op9frw+FQXV3dTuyblYff/jH4x/vf3tfEko3U0Ko9/u3XN//14nf//dk/l3zdeDwei8Xi//i/mUgk71UMGYbZqa+LNxwyfJ//6CgR6Ta+0tUZGCap0WD2EkoDCQ7lEw6t/8fVj9fCG9/vhv4PrbkOvSrZbP33f3vyzu9C8Ye7yTgRuUxPHj6cmmjW6+sef/wpIrr35YWfe+8mssr46uoMdXUG+m7233+58mDn+41H33y3sx1L7jLE/DL+ayLSfH3zP33953/9lMRL6/V6vV4f/faBkovQajSaus9uMf7fx598QtH7j8cbG3+gqCWAMkhwKI/du/f/6cZXv1l68Lvt3YcMyRXf/eNf/fJvpxkmySTl2xDR4sjs33yYqwHd+v3f/f03FE8m4kz85L+afauJaHPcsbRARAwx/3V98a+felb2yYpnq+P/8L+SwWDit/+krDVKCaHEkOCwf5hkkmGYZDzyh6k/LP/fLd+n278O7YazR80cPmHzUNRs8UYgGmEfmk+dZUvJmwZGzQtvbhMRJTe+WHjm2Q6F70NeYtVL0Z3k/c099wRQDMzHwf7RaLVanU7/WPTW5cD/+J/f/f1W7In/cKJdwRPtoy1K0lVZM5PVxj065kidUX/vy5CCV8iHCT8kIty8DSoFCQ77L/7d97Enhv/i+pe9//lMnquS2Ec75ny9l/faLBS4K7XYZpK9uEqR2HMxca48VAhmUWD/NQ1/2auoma+EzQBqAMbgcBCZrCekFvtDa+XeEoD9hASHA+moU7jCVSjg5x6t+1Jz30878l9lFqDaIcHhQBIdtNy+doUtFdmcYgtRiIjMx20SzwJQGcyDw8HUeaSDNriiw+mlnun0tf0nXkWCwwGAMTgcUE3D8y0ylSdChTgUArenqEJIcDiwbM2XfR2nMm7t098253sOA/AiMQyDHK8qGvw8ADIErdzlCy0Bb0laKu+wakkGRRH3zIPSwjw4AOSRHd98dIuXI80rAAkOALkxOYfaCO5KQoIDQG7I6OqFI5kAAGqFBAcAUCskOACAWiHBAQDUCgkOAKBWSHAAALVCggMAqBUSHABArZDgAABqhXMyoczWP/j8LHunBVfLlY+aj2WuD3348sK1FdGC/ra5t2QvBpuvt8KaAagMxuBQVv7Vt1M3ysniud3jSI9vIppe6nHcXiyit0KbAagOEhzKx7/6Rtcd+XsNb46f2ZBZtTF2YbPA3gpsBqBGSHAoj8ULsz25k9Rzf0F43N825+ud87V1CEum74uH4fl7K6QZgFphHhz23+a4Y2khX6PFj4UBuHAXtKaBUfMCNwGy8YXnmWc7lfamuBmAmmEMDuVkH23pyN/KZOXvgia65Tzd84WK6k1pMwD1QYJDedhHO+Z8vZfPmGTWhwJ3pRbbTJJ3K87XW2HNANQKsyiw/5qGfb1l7620LwpQlTAGh+pgsp6QWuwP4TgkgCwkOFSJo04z/zAU8HOP1kVz3087MBkCkA4JDlVCdNBy+9oVtvp7cyp1Jo75uE3iWQA1DfPgUC06j3TQBlf/N73UM52+tv/Eq0hwgAwYg0PVaBqeb5GsPBFViAOACBIcqoit+bKv45QrfWF/25zvOQzAASRoGIap9DYAVJeg1ck+sAS8JWmpvEOAgmAMDgCgVkhwAAC1QoIDAKgVEhwAQK2Q4AAAaoUEBwBQKyQ4AIBaIcEBANQKCQ4AoFZIcAAAtUKCAwCoFa4uC2WSmDi5NbYiWtDXcHE1UgVLcK0SUC+MwQEA1AoJDgCgVri6LEAmXF0W1AJjcAAAtUKCAwCoFRIcAECtkOAAAGqFBAcAUCskOACAWiHBAQDUCgkOAKBWSHAAALVCggMAqBWuTQjVaf2Dz8++uU1E5Gq58lHzscz1oQ9fXrgmvthgf9vcW00l6u29lpy9AVQLjMGhGvlX32YDV5Lndo8jPb6JaHqpx3F7sQy9AVQPJDhUHf/qG1131mRXb46f2ZBZtTF2YXN/ewOoKkhwqCqLF2Z7cgUukef+gvC4v23O1zvna+sQlkzfFw+cS9sbQNVBgkPV2Bx3zI5N52m0+LEwZDafOstOVTcNjJr5hRtfePajN4CqhASHKmQfbenI38pktXGPjjlMwtJ7vtC+9gZQRZDgUFXsox1zvt7LZ0wy60OBu1KLbSb7/vcGUHVQTQhVo2nY11utvQFUJYzBQVVM1hNSi/2hXIcry9QbQNkhwUFdjjqFw4yhgJ97tC6arX7aITdnsu+9AZQbEhzURXSYcfvaFbZee3MqdcKO+bhN4lnl6Q2g3DAPDirTeaSDNrgi7umlnox6wf4TrxaUuaXtDaDMMAYHtWkanm+RqRURaror1RtAeSHBQX1szZd9Hadc6Qv72+Z8zxUzZC5tbwDlpGEYptLbAKBWQauTfWAJePfeDKBQGIMDAKgVEhwAQK2Q4AAAaoUEBwBQKyQ4AIBaIcEBANQKCQ4AoFZIcAAAtUKCAwCoFRIcAECtkOAAAGqFBAcAUCtcHxyq0/oHn59l77TgarnyUfOxzPWhD19euLYiWtDfNveW7MVg8/VWWDOAaoExOFQj/+rbqRvlZPHc7nGkxzcRTS/1OG4vFtFboc0AqgcSHKqOf/WNrjvy9xreHD+zIbNqY+zCZoG9FdgMoKogwaGqLF6Y7cmdpJ77C8Lj/rY5X++cr61DWDJ9XzwMz99bIc0Aqg7mwaFqbI47lhbyNVr8WBiAC3dBaxoYNS9wEyAbX3ieebZTaW+KmwFUJYzBoQrZR1s68rcyWfm7oIluOU/3fKGielPaDKCKIMGhqthHO+Z8vZfPmGTWhwJ3pRbbTJJ3K87XW2HNAKoOZlGgajQN+3rL3ltpXxSgvDAGB1UxWU9ILfaHcBwSahESHNTlqNPMPwwF/NyjddHc99MOTIZAzUCCg7qIDlpuX7vCVn9vTqXOxDEft0k8C+Bgwjw4qEznkQ7a4Or/ppd6ptPX9p94FQkOtQNjcFCbpuH5FsnKE1GFOEBtQIKD+tiaL/s6TrnSF/a3zfmewwAcaouGYZhKbwOAWgWtTvaBJeDdezOAQmEMDgCgVkhwAAC1QoIDAKgVEhwAQK2Q4AAAaoUEBwBQKyQ4AIBa4ax6qJjExMmtMfH9ivsaLq5GqmAJqrZBLTAGBwBQKyQ4AIBa4ax6gOLhrHqoLIzBAQDUCgkOAKBWSHAAALVCggMAqBUSHABArZDgAABqhQQHKJ4l4GX/VXpDipGYOBm0OoPWkZjMqu0Jf6F9xs47g1Zn0OoMz5dkGyEPnFUPsO/UFvGeR2MrRBQfez825DaI18yPBE/PpDfuMwb4NmtXo1Pc0tivPNTVmfOJRK0jxt4b4bRrG0h1C/KQ4ABi6x98fvbNbSIiV8uVj5qPZa4PffjywjVx5PS3zb3VlNWNwmZVqtM42Rc8PUM0E514zTCk8PbR/ug5d1z4v6mh8EteY1exm9Dq1AmPJdOfiFpHGm8M6iRW1BDMogCk+FffZuNbkud2jyM9l4loeqnHcXuxiGZVxh/t5iZAglankJjxsReEheF5oi63MHFkmewjSkVtYmI4skxEroZbXuMAEVHstGh+hn0i+xRyNdzyWgJey41Bw9D1VIcBryXAPVeRZfeW9WR0rSRvX62Q4AAc/+obXXfk82Bz/MyGzKqNsQubBTbbE3+0u5hJagE7W81fGHImbHUGz99U/tJsmid8q6nF8yNsb/qL4/V2MlyaMLA9d19NiF/3V+wXQ7PWLizzhK3O4ubciYhoJfKep6gnHhBIcAAiWrww25Mrvok89xeEx/1tc77eOV9bh7Bk+v5iQc2KND8StDqD1hciy3vqRoq9/oY3YzicOTruIiJ/fJmIXHohglvsOmGWo3XkMDfl0mm8NaIndpgsjMT9yTtERDTwYvYEt9ZhS2vTYpeYHmkdaeQ25tOGVn7hnbVEdsuagQSHmrc57pgdm87TaPFjYWRtPnWWndFuGhg18ws3vvAU0KxQ3EBVejq4cIZL4hDsMwa8lkv8Ucf5kaBo4JyYOBlMH0cLEqvsEP6TsLBVy+4tYR6mXZgT50fiazdjy0RE+mbRxPraWrKYd2Cr/0VfMc87cJDgAAL7aEtH/lYmK59AxxwmYek9X6ioZjnxxXlDmQV/qdFusfg8Fc11+KPdzuDpmdTAmZ0bWXZvCbMcXOCmpkH0za8ZJ/uodaRBav5af3HEQH3GG4M6osRnN+JERC7D8zm2nB3jp6e8BI/wtaHv/VktH8xELQoAEdlHOy6fMRFtjr8puT4UuCu12GayE60V3EwRTzg7uEtXY8fnKRGxY2d3at3ABDck73Jbbjm3291x9pDm6oTldam+utyWLiIarL8ktXaI/Y9/d5Yds69E2p0R4YVe8rKxnpqWySFjO6kU32QqhwSHmtc07Out9Dbk4Wq4db1eKuOKu1OdMfBiLLXEpW9diS/3GScpfJoyvyHsg+bAYGLi5NZsd+OlTpr/JE5ENBO2popVtulTMxej/mj3C5FlMkx6jV3ctukvfmoesomG/JJEsc53GxzL83XF9VzbMIsCoIDJekJqsT+0Vkyzgq1E2p1y508WIX5+KEakb3UREVGzodelv/iaocttCbgNa1e3UyV6/mi3M3jeoxu6bmFnQsT1JyKx885g99UE2ep6XUSU9PmJnyiPr/opbcjfZxQfh8xBXBIu+S5Wi6/GOTCQ4ABKHHUKRyNDAT451kWT2k87TMqbKdEplXQz3CFNmaOLhegz8Hse2ufP1bNz02tXt9vdcaFEb/79yDLR1JBQ6qdLK9/mNk/r8MemiJbdj+ZJ52gmovjszQRfVWJ4qZNShz2ziAvM85aEs7UobJULpW1YzUKCAyghOhq5fe0KW9a9OZU6/cd83FZAM4VsXIWfkFmCZffDCT9lRqrXEnDXK1jyWLNLf/G1OqE3e6eBnaKxDx6+6CIimno3uuaPvpNRI8jJumpK56GLLiKKvXM10fWigYiWvQlu2oSb4OYrxEvBPmjmzgyi+NgwzugBgPw6j4jKupd6HLM9jiVR6feJV22FNCuMfdAc8FoC3kY2XvdM5zhXLzODrBsab2glopVIO1d1bvhF6sz19FOBRM96vltPRMs3dtds+lYimom9540TUWt3HTd932mczK7/W0s7EVT5JbG63Pw4fSVybu+7IyqGBAdQpml4vkWmYEIo/VberCj8iFvZPHIOXZ3yI2Jb/buiIf/AhPjaJrpmFxEZJr2WgNc8RKmze+yD9QNErc1afr/BQDNEMifm5JHzpB5ealDP747UJtSiAChla77sa8p/ySqFzfayIfU3vPWl6ixDxmWkpt6Nvt4plMHohq5bhqSfZ7jktaT+L20SPF2qjoU9ETTrjfij7yjZUOHyWxQfeyHs2MNVtNRMwzBMpbcBACqAr0Tki/a4w5gcw0BfbIqPWvFVADOvFMiWIeY6WZQr+8u+xKBQeJ6GL4SXXgtpMIsCAP5ot+g8+NaRxoDXeMmdmq5hT5c/7yEisjvFe+6GyULPMJKsJuQvGyA6ATXfaZlAhDE4QM1KH4P7o90vREjyituesHUotr8jYu5UoBQMwJVBggMAqBVmUQAA1AoJDgCgVkhwAAC1QoIDAKgVEhwAQK2Q4AAAaoUEBwBQKyQ4AIBa/X+zARwfo4+QfwAAAABJRU5ErkJggg==" alt="" />

按 1. CRC 算法原理 所述，将长度为 k 位的数据块对应一个GF(2)多项式M，以 8 位数据块11100110举例，如果先传输MSB（Most Significant Bit），则它对应的多项式为x^7 + x^6 + x^5 + x^2 + x （8位对应x的7次幂，因为从x⁰ 开始计数，2进制为1时有效）。发送端和接收端约定一个次数为 r 的CRC多项式，取CRC-4 为例：x^4 + x + 1，r = 4。在数据块后面加上r个0对应的多项式为M'，显然有M' = Mx^r 。用 M' 除以CRC-4 将得到一个次数等于或小于 r-1 的余数多项式 R，其对应的 r 位数值则为校验码。发送方通过指定的CRC多项式产生r位的CRC校验码，接收方则通过该CRC多项式来验证收到的报文码的CRC校验码是否为0。

具体推算如下：

设CRC多项式为G(x)：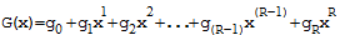

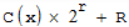假设发送信息用信息多项式C(x)表示，将C(x)左移 r 位，则可表示成C(x)x^r，这样C(x)的右边就会空出r位校验码的位置，使用GF(2)（模2除法），得到的余数R就是校验码。发送的CRC编码是, 至于验证接收到的报文编码是否至正确，方法依然是做模2除：，若余数为0则正确。

2.2 逻辑异或运算

CRC校验是基于多项式进行的运算，其加减法运算以2为模GF(2) ，加减时不进（借）位，实际上与逻辑异或（XOR）运算是一致, XOR是将参加运算的两个数据，按二进制位进行“异或”运算。

异或运算规则（^）规则如下：

0^0=0；  0^1=1；  1^0=1；   1^1=0；

即：参加运算的两个对象，如果两个相应位为“异”（值不同），则该位结果为1，否则为0。

2.3 传输计算示例

以G(X)=X⁴+X³+1为例，设原数据为10110011。

（1）G(X)=X⁴+X³+1, 二进制比特串为11001。（在 X 的n 次方不为0处2的n次方的位=1 )

（2）因为校验码4位，所以10110011后面需加4个0，得到101100110000，用“模2除法” (即逻辑亦或^) 即可得出结果：

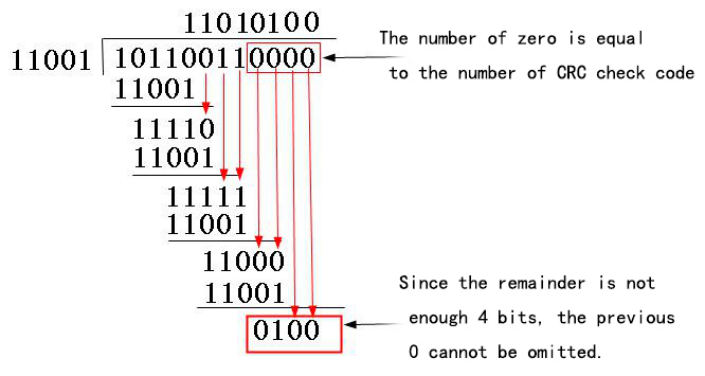
（3）即CRC^101100110000得到101100110100，并发送到接收端。

（4）接收端收到101100110100后除以11001(以“模2除法”方式去除),余数为0则无差错。

3. CRC 的实现（Reversed 反向校验模式）

一般来说CRC有多种实现方式，在本文中我们以C语言为例，并给出 直接生成法 和 查表法 两个例子。

直接生成法 适用于 CRC 次幂较小的格式，当CRC 次幂逐渐增高时，因为其复杂的Xor 逻辑运算会拖累系统运行速度，不再建议使用直接生成法，取而代之的是查表法——将数据块M 的一部分提前运算好，并将结果存入数组中，系统开始执行运算时，相当于省去了之前的操作，直接从类似中间的位置开始计算，所以会提高效率。

在计算CRC时也可以选择正向校验（Normal） 或者反向校验（Reversed），由于 Normal 和 Reversed 是镜像关系，两种方法会影响到最后的校验码，使得两种方式最后得到的校验码呈现镜像关系。 但这对CRC 本身的成功率并没有影响，只不过是： 正向走一遍，还是镜像走一遍罢了。

那为什么还会有Reversed格式呢？ 是因为在大多数硬件系统的传输中，普遍先发送LSB，而Reversed 的CRC 正是满足于这种LSB First 的格式，因此适用。

下面为计算过程：

设数据块为Mx, CRC校验式为G(x) FCS位数为 r。

如下表所示，当采取反向校验设计时, 需进行以下操作：

Name	Polynomial Representations
	Normal	Reversed	Reciprocal	Reversed reciprocal
CRC-3-GSM	0x3	0x6	0x5	0x5
CRC-8	0xD5	0xAB	0x57	0xEA
CRC-16-CCITT	0x1021	0x8408	0x811	0x8810
CRC-32	0x04C11DB7	0xEDB88320	0xDB710641	0x82608EDB

（1）将翻转后的Mx^r的后r位放入一个长度为r的寄存器中；

（2）如果寄存器的首位为1，将寄存器右移1位(将Mx^r剩下部分的MSB移入寄存器的MSB（高八位）)，再与G(x) 的后r位异或，否则仅将寄存器右移1位(将Mx^r剩下部分的LSB（低八位）移入寄存器的LSB)；

（3）重复第2步，直到M全部 Mx^r 移入寄存器；

（4）寄存器中的值则为校验码。

代码如下（基于C语言）：

unsigned int CRC;//int的大小是32位，作32位CRC寄存器
unsigned int CRC_32_Table[];//用来保存CRC码表
void GenerateCRC32_Table()
{
   for(int i=;i<;++i)//用++i以提高效率
{      CRC=i;
       for(int j=;j<;++j)
         {
           if(CRC&)// LSM为1
           CRC=(CRC>>)^0xEDB88320;//采取反向校验
           else //0xEDB88320就是CRC-32多项表达式的reversed值
            CRC>>=;
         }
     CRC_32_Table[i]=CRC;
  }
}

4. 生成多项式的选择

不同的CRC生成多项式，其检错能力是不同的。要使用R位校验码，生成多项式的次幂应为R。同时生成多项式应该包含项"1"，否则校验码的LSB(Least Significant Bit)将始终为0。如果数据块M (包括校验码) 在传输过程中产生了差错，则接收端收到的消息可以表示为M +R’。若R’ 不能被CRC 生成多项式G 除尽，则该差错可以被检测出。考虑以下几种情况：

1) 1位差错，即R’ = x^n = 100...00，n >= 0。只要G至少有2位1，R'就不能被G除尽。这是因为G x^k相当于将G左移k位，对任意多项式Q，QG相当于将多个不同的G的左移相加。如果G至少有两位1，它的多个不同的左移相加结果至少有两位1。

2)奇数位差错，只要G含有因子F = x + 1,  R' 就不能被G除尽。这是因为QG = Q'F，由1)的分析，F的多个不同的左移相加结果1的位数必然是偶数。

3)爆炸性差错，即R' = (x^n + ... + 1)x^m = 1...100...00，n >= 1，m >= 0，显然只要G包含项"1"，且次数大于n，就不能除尽R'。

4)2位差错，即R' = (x^n + 1)x^m = 100...00100...00，n >= 0。设x^n + 1 = QG + R，则R' = QGx^m + Rx^m，由3)可知R'能被G除尽当且仅当R为0。因此只需分析x^n + 1，对于次数R，总存在一个生成多项式G，使得n最小为2^R - 1时，才能除尽x^n + 1。称该生成多项式是原始的(primitive)，它提供了在该次数上检测2位差错的最高能力，因为当n = 2^R - 1时，x^n + 1能被任何R次多项式除尽。

-----------------------------------------------------------------------这又是一条华丽的分界线---------------------------------------------------------------------------------------

5. Q & A

Q: 为什么寄存器初始化置0？

A: 寄存器的初始值不为 0，那么寄存器中的值就相当于是待测数据，这样算出的 CRC 结果并不正确。再考虑CRC32 模型的 Init=0xFFFFFFFF，待测数据的内容和长度为随机，如果寄存器初始值为 0，那么待测字节则为 1 字节 0x00，计算出来的 CRC32 值也就为 0。寄存器用0xFFFFFFFF 进行初始化，就可以避免这个问题

Q：为什么先移位再XOR？

A: 0xEDB88320已经是Gx 去掉最高项的简写，为了确保运算无误，所以需要先移位再XOR。这不会影响最后的结果，因为在做XOR运算时，gx 的最高位都会被消掉（因为在除法运算中每次循环都是从1 开始除， 而gx 的最高项就是1，所以每次都会被消掉）

Q: 查表法的index 是什么，而内容又是什么？

A: Index 为数据块M 的前8位，内容是前8位与CRC XOR后的值，用时需再与gx异或。

Q: 查表法为什么会有256个字符？

A: 在CRC-16和32中，一次移出的待测数据为 8 位 bits，即一次进行一个字节的计算，则表格有 2^8＝256 个表值。一个字节有8位二进制数，每一位都有2种选择。

6. 参考资料推荐

https://bbs.pediy.com/thread-17195.htm  （通俗解释）

https://www.cnblogs.com/bugutian/p/6221783.html（解释移位原理）

https://blog.csdn.net/mish84/article/details/27528125（解释代码）