利用划分树求解整数区间内第K大的值

如何快速求出（在log2n的时间复杂度内）整数区间[x,y]中第k大的值（x<=k<=y）?

其实我刚开始想的是用快排来查找，但是其实这样是不行的，因为会破坏原序列，就算另外一个数组来存储，多次询问的条件下，同样满足不了。

划分树主要是针对上述问题而设计的。 划分树是一种基于线段树的数据结构，其基本思想就是将待查找的区间分为两个子区间：不大于数列中间 值的元素被分配到左儿子的子区间，简称左子区间；大于数列中间值的元素被分配到右儿子的子区间，简称右子区间。

显然，左子区间的数小于右子区间的数。建树 的时候要注意，对于被分到同一子树的元素，元素间的相对位置不能改变。例如构建整数序列[1 5 2 3 6 4 7 3 0 0]的划分树：

整数序列经排序后得到[0 0 1 2 3 3 4 5 6 7]，中间值是3。划分出下一层的左子区间[1 2 3 0 0]，中间值为1；下一层的由子区间[5 6 4 7 3]，中间值为5；以中间值为界，划分出当前层每个区间的下层左右子区间······以此类推，直至划分出所有子区间含单个整数为止。

这里可能有人就会提问了，为什么两个子区间是这样的呢？？  其实我刚开始也这么想，下面给出解释：

1.如果有和中间值相等的元素，插入进去的前提是  小于中间值的元素不够填满一个区间，差多少就补多少和中间值相等的元素（很好理解，小于肯定优先嘛）。

2.相对位置不能改变。

下面给出一个图，还是以[1 5 2 3 6 4 7 3 0 0]为例：

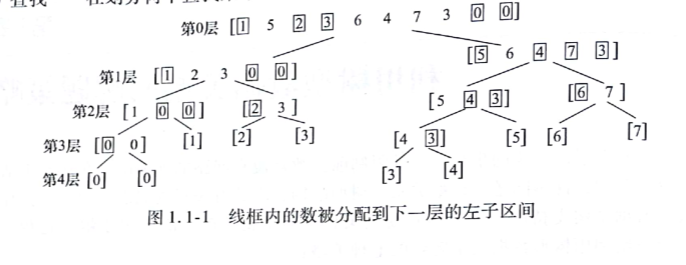
如图可见，划分树是一颗完全二叉树，树叶为单元素区间。若数列含有n个整数，则对应的划分树有[log 2 n]+1层。

查找的时候通过记录进入左子树的数的个数，确定下一个查找区间，直至查找范围缩小到单元素为止。  此时，区间内的第K大值就找到了。

整个算法分两步：

1.建树-------离线构建整个查询区间的划分树

2.查找-------在划分树中查找某个子区间中的第K大值。

在查询之前，我们先离线构建整个查询区间的划分树。  建树过程比较简单，对于区间[l,r],首先通过对原数列排序找到这个区间的中间值的位置mid(mid=[(l+r)/2]),不大于中间值的数划入左子树[l,mid], 大于中间值的数划入右子树[mid+1,r] 。同时，对于第i 个数，记录在[l,i] 区间内有多少整数被划入左子树。  最后继续对它的左子树[l,mid]  和右子树[mid+1,r]  递归建树，直至划分出最后一层的叶节点为止，显然，建树过程是自上而下的。

具体实现办法：

先将读入的数据排序成sorted[]   (从小到大排序) ,取区间[l,r]的中间值sorted[mid]，然后遍历[l,r]区间，依次将每个整数划分到左子区间或者右子区间中去。  注意，被分到每个子树的整数是相对有序的。  注意，这里要记录区间能插入多少个和中间值相等的元素。    另外，在这个过程中，要记录一个类似前缀和的东西，即  l  到  i  这个区间内有多少整数被划分到左子树。设：

tree [p][i] ------第p层第i个位置的整数值，初始序列为tree[0][]。

sorted[]---------排序序列，即存储tree[0][]排序后的结果

toleftp[][]--------toleft[p][i],表示第p层前i个数中有多少个整数分入下一层的左子区间

lpos和rpos-----下一层左子区间和右子区间的指针

same------------当前区间等于中间值的个数

下面给出建树的具体代码：

void Build(int l,int r,int dep)//左边界 右边界 第几层
{
    if(l==r) return ;
    int mid=(l+r)>>;
    int same=(mid-l+);//左子树可以有多少个等于mid的数
    for(int i=l;i<=r;i++)
    {
        if(tree[dep][i]<sorted[mid])
            same--;//计算可以放多少个等于mid值的数，保证相对位置不变
    }
    int lpos=l;
    int rpos=mid+;
    for(int i=l;i<=r;i++)
    {
        if(tree[dep][i]<sorted[mid])
        {
            tree[dep+][lpos++]=tree[dep][i];
        }
        else if(tree[dep][i]==sorted[mid]&&same>)
        {
            tree[dep+][lpos++]=tree[dep][i];
            same--;
        }
        else
        {
            tree[dep+][rpos++]=tree[dep][i];
        }
        toleft[dep][i]=toleft[dep][l-]+lpos-l;
    }
    Build(l,mid,dep+);
    Build(mid+,r,dep+);
}

　　在划分树上查询子区间[l,r]中第K大的数呢？(L<=l,r<=R)? 我们从划分树根出发，自上而下查找：

　　若查询至叶子(l==r),则该整数(tree[dep][l]) 为子区间[l,r]中第K大的数；否则区间[L,l-1]内有toleft[dep][l-1]个整数进入下一层的左子树，区间[L,r]内有toleft[dep][r]个整数进入下一层的左子树。显然，在查询子区间[l,r]中有cnt=toleft[dep][r]-toleft[dep][l-1]个整数进入到下一层的左子树。如果cnt>=k，则递归查询左子树(对应区间[L,mid]）；否则递归查询右子树(对应区间[mid+1,R).。

　　难点是，如何在对应子树的大区间中计算被查询的子区间[newl,newr]?

　　若递归查询左子树，则当前子区间的左边是上一层[L,l-1]里的toleft[dep][l-1]-toleft[dep][L-1]个整数，由此可得到newl=L+toleft[dep][l-1]-toleft[dep][L-1]; 加上上一层查询区间[l,r]中cnt个整数，newr=newl+cnt-1(这里-1是为了处理边界问题，值得大家认真思索），即在大区间[L,mid]里查询子区间[newl,newr]中第K大值。（这里看文字有点抽象，最好看上面的图来理解）

　　同理，若递归查询右子树，则[l,r]中有r-l-cnt个整数进入右子树，需要计算其中第K-cnt大的整数值。关键是如何计算被查询子区间的右指针newr:

　　当上一层的[l,r]和[r+1,R]中有若干个整数被分配至下一层左子区间，其中[r+1,R]中有toleft[dep][R]-toleft[dep][r]个整数位于左子区间的右方，因此查询子区间的右指针移至r右方的第toleft[dep][R]-toleft[dep][r] 个位置,即newr=r+toleft[dep][R]-toleft[dep][r]。显然，左指针newl=newr-(r-l-cnt)。

下面给出具体实现的代码：

int query(int L,int R,int l,int r,int dep,int k)
{
    if(l==r) return tree[dep][l];
    int mid=(L+R)>>;
    int cnt=toleft[dep][r]-toleft[dep][l-];
    if(cnt>=k)
    {
        int newl=L+toleft[dep][l-]-toleft[dep][L-];
        int newr=newl+cnt-;
        return query(L,mid,newl,newr,dep+,k);
    }
    else
    {
        int newr=r+toleft[dep][R]-toleft[dep][r];//相当于把r挤到这个位置
        int newl=newr-(r-l-cnt);
        return query(mid+,R,newl,newr,dep+,kcnt);
    }
}