最短路【洛谷P1841】 [JSOI2007]重要的城市

P1841 [JSOI2007]重要的城市

题目描述

参加jsoi冬令营的同学最近发现，由于南航校内修路截断了原来通向计算中心的路，导致去的路程比原先增加了近一公里。而食堂门前施工虽然也截断了原来通向计算中心的路，却没有使路程增加，因为可以找到同样长度的路作替代。其实，问题的关键在于，路截断的地方是交通要点。

同样的情况也出现在城市间的交通中。某些城市如果出了问题，可能会引起其他很多城市的交通不便。另一些城市则影响不到别的城市的交通。jsoi冬令营的同学发现这是一个有趣的问题，于是决定研究这个问题。

他们认为这样的城市是重要的：如果一个城市c被破坏后，存在两个不同的城市a和b（a, b均不等于c），a到b的最短距离增长了（或不通），则城市c是重要的。

jsoi冬令营的同学面对着一张教练组交给他们的城市间交通图，他们希望能找出所有重要的城市。现在就请你来解决这个问题。

输入输出格式

输入格式：

第一行两个整数N,M,N为城市数，M为道路数

接下来M行，每行三个整数，表示两个城市之间的无向边，以及之间的路的长度

输出格式：

一行，按递增次序输出若干的数，表示重要的城市。

Floyd好题。

一开始没读懂题意，感觉一眼傻逼题。直接枚举中间点判断就行了。

但是只有60分。

因为根据这个题的定义，如果存在这种情况：i到j之间有两条相等长度的最短路，那么这两条路上的所有点都不能被算为重要城市。

但是根据我一开始的做法，这些在某两个点之间的最短路上的点都是重要城市。

这里就有一个Floyd的知识了。

就是我们对于每一个点对，都会有一个中间点去更新这两个点的最短距离。

我一直对这个中转点的概念比较模糊，一直以为两个点之间有很多中转点。

但是ZAGER大佬给我讲说，可以很直观地发现，每一个点对最终都会只有唯一一个中转点。

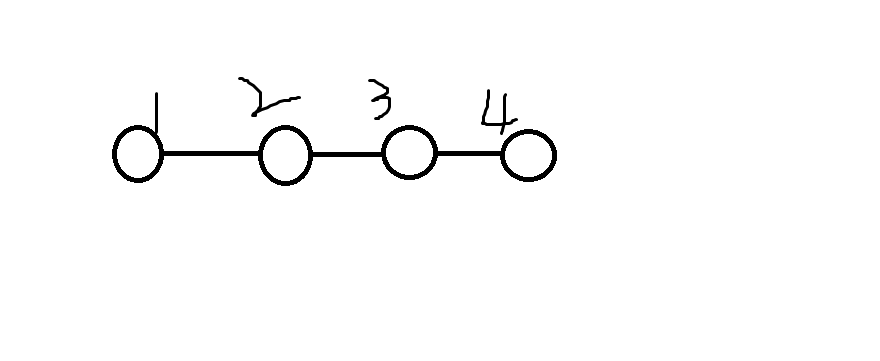
就像上图，1到4之间中转点只会是3，因为最后更新1到4的答案的是3，那么2呢？2会作为1到3的中转点。

所以对于这道题，我们只需要记录一下每个点对的中转点，如果有重复的，那么这些重复点都不是，没有的话，这些中转点就是答案中的点。

还是太菜了。。。

code：

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

const int wx=1107;

inline int read(){
	int sum=0,f=1; char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
	while(ch>='0'&&ch<='9'){sum=(sum<<1)+(sum<<3)+ch-'0'; ch=getchar();}
	return sum*f;
}

int n,m,tot;
int dis[wx][wx];
int ans[wx],mid[wx][wx];
int flag[wx][wx];

int main(){
	n=read(); m=read();
	memset(dis,0x3f,sizeof dis);
	for(int i=1;i<=n;i++)dis[i][i]=0;
	for(int i=1;i<=m;i++){
		int x,y,z;
		x=read(); y=read(); z=read();
		dis[x][y]=dis[y][x]=min(z,dis[x][y]);
	}
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
//				dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
				if(i!=j&&j!=k&&i!=k&&dis[i][j]>dis[i][k]+dis[k][j]){
					dis[i][j]=dis[i][k]+dis[k][j];
					mid[i][j]=mid[j][i]=k;
				}
				else if(dis[i][k]+dis[k][j]==dis[i][j]&&i!=j&&i!=k&&k!=j){
					mid[i][j]=0;
				}
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			ans[mid[i][j]]=1;
		}
	}
	for(int i=1;i<=n;i++){
		if(ans[i])printf("%d ",i),tot++;
	}
	if(!tot)puts("No important cities.");
    return 0;
}