POJ 3734 Blocks （线性递推）

定义a_i表示红色和绿色方块中方块数为偶数的颜色有i个，i = 0,1,2。

_aij表示刷到第j个方块时的方案数，这是一个线性递推关系。

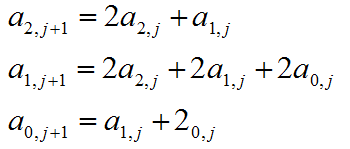
可以构造递推矩阵A，用矩阵快速幂求解。

 /*********************************************************
 *            ------------------                          *
 *   author AbyssalFish                                   *
 **********************************************************/
 #include<cstdio>
 #include<iostream>
 #include<string>
 #include<cstring>
 #include<queue>
 #include<vector>
 #include<stack>
 #include<vector>
 #include<map>
 #include<set>
 #include<algorithm>
 #include<cmath>
 using namespace std;

 typedef long long ll;

 #define PB push_back
 const int maxn = , mod = 1e4+;
 const int n = ;
 typedef int MType;
 typedef vector<MType> row;
 typedef vector<row> mat;
 struct Matrix
 {
     mat dat;
     row &operator [](int x){ return dat[x]; }
     Matrix operator * (Matrix& B) {
         Matrix re;
         re.dat.resize(n,row(,));
         for(int i = ; i < n; i++){
             for(int j = ; j < n; j++){
                 for(int k = ; k < n; k++){
                     re[i][j] = (re[i][j]+dat[i][k]*B[k][j])%mod;
                 }
             }
         }
         return re;
     }
     Matrix operator ^ (int q){
         Matrix Re, A = *this;
         Re.dat.resize(n,row(,));
         for(int i = ; i < n; i++) {
             Re[i][i] = ;
         }
         while(q){
             if(q&){
                 Re = Re * A;
             }
             A = A * A;
             q >>= ;
         }
         return Re;
     }
 };

 //#define LOCAL
 int main()
 {
 #ifdef LOCAL
     freopen("in.txt","r",stdin);
 #endif
     Matrix A;
     A.dat.resize(,row(,));
     A[][] = ; A[][] = ;
     fill(A.dat[].begin(),A.dat[].end(),);
     A[][] = ; A[][] = ;
     int T; scanf("%d",&T);
     while(T--){
         int N; scanf("%d",&N);
         //mat R = .dat;+R[0][1]+R[0][2]
         printf("%d\n", (A^N)[][]);
     }
     return ;
 }

矩阵

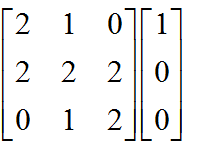
由初值可知，最后答案为A^k(1,1)，复杂度是O(3^3*logN)。

如果利用特征值的话，效率会更高。

A的对角化矩阵Λ为

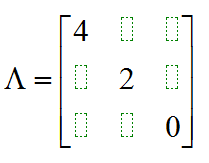
如果对应的特征向量矩阵为P，A^k = P * Λ^k * P'。

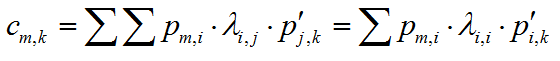
因为除了对角元都为0，所以可以去掉一个和号，而特征值4对应的系数为1/4，2对应的系数为1/2，因此最终答案为4^n-1+2^n-1。

 /*********************************************************
 *            ------------------                          *
 *   author AbyssalFish                                   *
 **********************************************************/
 #include<cstdio>
 #include<iostream>
 #include<string>
 #include<cstring>
 #include<queue>
 #include<vector>
 #include<stack>
 #include<vector>
 #include<map>
 #include<set>
 #include<algorithm>
 #include<cmath>
 using namespace std;

 const int mod = 1e4+;
 int pow_mod(int a,int q)
 {
     int re = ;
     while(q){
         if(q&) re = (re*a)%mod;
         a = (a*a)%mod;
         q>>=;
     }
     return re;
 }
 //#define LOCAL
 int main()
 {
 #ifdef LOCAL
     freopen("in.txt","r",stdin);
 #endif
     int T; scanf("%d",&T);
     while(T--){
         int N; scanf("%d",&N);
         printf("%d\n",(pow_mod(,N-)+pow_mod(,N-))%mod);
     }
     return ;
 }