JML契约式设计——第三单元学习小结

一、前言

---

　　本单元作业都是关于JML(Java Modeling Language)，JML是一种契约式设计(Design by Contract)的语言，契约式设计的主要目的是希望程序员能够在设计程序时明确地规定一个模块单元（具体到面向对象，就是一个类的实例）在调用某个操作前后应当属于何种状态，它强调三个概念：前置条件，后置条件和不变式，要求输入的参数满足前置条件，要求函数完成时的状态满足后置条件，要求函数开始运行和结束运行时满足不变式，即对调用者来说不变式总是为真，而对函数内部来说不变式可以为假。对JML来说，前置条件就是requires限定的条件，后置条件就是ensure限定的条件，不变式则是invariant限定的条件，其他的语句像assignable等都是为这几个条件服务的。

　　本次作业即是基于JML，给出程序运行框架，把几个方法“挖空”，然后给出这几个方法的JML规格，让我们“按图索骥”。只是这“骥”是千里马还是下等马，还是要靠自己的代码功底及完善的单元测试决定。本次作业用到的工具有：idea, jdk, Junit, OpenJML, JMLUnitNG,SMT Solver等。

二、JMLUnitNG的使用

---

　　经过一下午的尝试，发现JMLUnitNG确实有点不好用，也可能是我不会用，他连一些新写法的JAVA语法都检查不通过，因此我只好写了个简单的测试文件：

import java.util.ArrayList;

public class JMLUnitNG {
    public ArrayList<Integer> array = new ArrayList<Integer>();

    public JMLUnitNG() {
        /*array.add(12);
        array.add(23);*/
    }

    public void addIncrease(int ele) {
        for (int i = 0; i < array.size(); i++) {
            if (array.get(i) > ele) {
                array.add(i, ele);
            }
        }

    }

    public void remove() {
        array.remove(0);
    }

    public int addFirstAndSecond() {
        return array.get(0) + array.get(1);
    }

    public int multFirstAndSecond() {
        return array.get(0) * array.get(1);
    }

    public static void main(String[] args) {
        JMLUnitNG unit = new JMLUnitNG();
    }
}

得到测试结果：

Failed: racEnabled()
Passed: constructor JMLUnitNG()
Failed: <<JMLUnitNG@6fdb1f78>>.addFirstAndSecond()
Passed: <<JMLUnitNG@4fccd51b>>.addIncrease(-2147483648)
Passed: <<JMLUnitNG@4ca8195f>>.addIncrease(0)
Passed: <<JMLUnitNG@65e579dc>>.addIncrease(2147483647)
Failed: <<JMLUnitNG@61baa894>>.multFirstAndSecond()
Failed: <<JMLUnitNG@b065c63>>.remove()
Passed: static main(null)
Passed: static main({})

===============================================
Command line suite
Total tests run: 10, Failures: 4, Skips: 0
===============================================

但他的测试数据也太简单了吧，基本没啥用，并且当我把构造方法的注释取消以后，连结果都运行不出来了，只有如下三行：

 Failed: racEnabled()
Passed: constructor JMLUnitNG()
Passed: <<JMLUnitNG@5f5a92bb>>.addFirstAndSecond()

三、SMT Solver

---

　　测试代码：

public class Path {
    public int[] nodes;

    //@ ensures \result == nodes.length;
    public /*@ pure @*/ int size() {
        return nodes.length;
    }

    /*@ requires index >= 0 && index < size();
      @ assignable \nothing;
      @ ensures \result == nodes[index];
      @*/
    public /*@ pure @*/ int getNode(int index) {
        return nodes[index];
    }

    /*@ public normal_behaviour
      @ ensures \result == nodes[i] - nodes[j];
    */
    public int compare(int i, int j) {
        return nodes[i] - nodes[j];
    }

    public static void main(String[] args) {

    }
}

　　然后 运行命令行：

java -jar .\openjml.jar -exec C:\Users\yang\Desktop\\openjml-0.8.-\Solvers-windows\z3-4.7..exe -esc C:\Users\yang\Desktop\\openjml-0.8.-\Path.java

　　得到结果：

C:\Users\yang\Desktop\1234\openjml-0.8.42-20190401\Path.java:4: 警告: The prover cannot establish an assertion (NullField) in method Path
public int[] nodes;
^
C:\Users\yang\Desktop\1234\openjml-0.8.42-20190401\Path.java:25: 警告: The prover cannot establish an assertion (ArithmeticOperationRange) in method compare: underflow in int difference
return nodes[i] - nodes[j];
^
C:\Users\yang\Desktop\1234\openjml-0.8.42-20190401\Path.java:25: 警告: The prover cannot establish an assertion (PossiblyNegativeIndex) in method compare
return nodes[i] - nodes[j];
^
C:\Users\yang\Desktop\1234\openjml-0.8.42-20190401\Path.java:25: 警告: The prover cannot establish an assertion (PossiblyTooLargeIndex) in method compare
return nodes[i] - nodes[j];
^
C:\Users\yang\Desktop\1234\openjml-0.8.42-20190401\Path.java:25: 警告: The prover cannot establish an assertion (ArithmeticOperationRange) in method compare: overflow in int difference
return nodes[i] - nodes[j];
^
C:\Users\yang\Desktop\1234\openjml-0.8.42-20190401\Path.java:25: 警告: The prover cannot establish an assertion (Postcondition: C:\Users\yang\Desktop\1234\openjml-0.8.42-20190401\Path.java:22: 注: ) in method compare
return nodes[i] - nodes[j];
^
C:\Users\yang\Desktop\1234\openjml-0.8.42-20190401\Path.java:22: 警告: Associated declaration: C:\Users\yang\Desktop\1234\openjml-0.8.42-20190401\Path.java:25: 注:
@ ensures \result == nodes[i] - nodes[j];
^
C:\Users\yang\Desktop\1234\openjml-0.8.42-20190401\Path.java:25: 警告: The prover cannot establish an assertion (PossiblyTooLargeIndex) in method compare
return nodes[i] - nodes[j];
^
C:\Users\yang\Desktop\1234\openjml-0.8.42-20190401\Path.java:25: 警告: The prover cannot establish an assertion (PossiblyNegativeIndex) in method compare
return nodes[i] - nodes[j];
^
9 个警告

可以看出大部分都是溢出警告，改了以后就没有警告了。

然后运行rac检查：

java -jar .\openjml.jar -exec C:\Users\yang\Desktop\1234\openjml-0.8.42-20190401\Solvers-windows\z3-4.7.1.exe -rac C:\Users\yang\Desktop\1234\openjml-0.8.42-20190401\Path.java

并未发生警告。

四、设计思路

---

　　第一次作业的思路很简单，分成两个类：Path和PathContainer，对于Path，我们要做的是查询Path的第i个元素，以及查询Path的不同的元素的个数，查询是否包含某个元素。在这里我们可以直接选择ArrayList把这些功能都完成，但是对于我们来说，速度也是很重要的，于是我们设计了两个容器，ArrayList和HashSet, ArrayList按顺序存放Path的元素，按索引查询就用这个，然后HashSet是存不同的元素的，将每一个元素加入HashSet，然后HashSet的size()方法返回值即是不同元素的个数，查询Path是否包含某元素也可直接用HashSet的contains方法查询。对于PathContainer，我们要做的是对完成一个Path的容器，实现增删改查的操作，用ArraryList容易超时，于是我选择了HashMap，将每条Path加入HashMap中，加路径，删路径，直接可以访问HashMap，时间复杂度很低。但是怎么查询Path呢，用ArrayList不是不可以，只是在执行删除操作以后不好处理其中的元素，于是我再建了一个HashMap将路径序号映射到Path，这样两个HashMap共同使用就可以完成这个容器类了。

　　第二次作业则变成了OO数据结构复习课，将我们的数据结构的图论知识复习了一遍，本次作业的需求是在第一次作业的基础上加了节点之间的最短距离，这就要用到Dijkstra或者floyd等算法了，然后我选择了floyd算法，首先floyd只需要在加或者删的时候计算一遍就OK，纵使他的复杂度有O(n^3)，我仍然觉得他在多条查询最短距离的情况下会比Dijkstra快，其次，floyd只需计算一次，就能将所有节点间的最短距离保存下来，之后查询就不需要耗费时间了，我觉得这更符合人的思维习惯。第三，floyd简单易懂，扩展性强。但是节点的编号可以是整个int的范围，这个用邻接矩阵必定会MLE，所以我们将节点编号映射到0-250的范围，再开一个250*250的矩阵，套用flyod算法，直接开花，直接得出结果。

　　第三次作业则是本次作业难度的分水岭，它加四个需求，最低票价，最少换乘次数，最少不满意度，以及连通块数量。这次在同学间在最低票价，最少换乘次数，最少不满意度的计算中就出现了Floyd和Dijkstra两大教派了，Floyd通过特殊的矩阵可以直接算出这三者，而Dijkstra可以通过拆点，缓存的手段，在每次查询中都计算一遍节点到节点的最低票价，最少换乘次数，最少不满意度以及最短距离，并缓存下来。这种方法听起来就很复杂，既然追求速度和简洁，那就要贯彻到底，于是我依旧是用了floyd算法。本次作业的floyd算法使用的矩阵是特殊的：

• 对于最少换乘次数，将每条路径内每两个节点之间的距离设为1，如图：

加入两条路径：1-2-3和4-1-3-5

第一步，将1-2-3路径的每两个点的距离设为1：

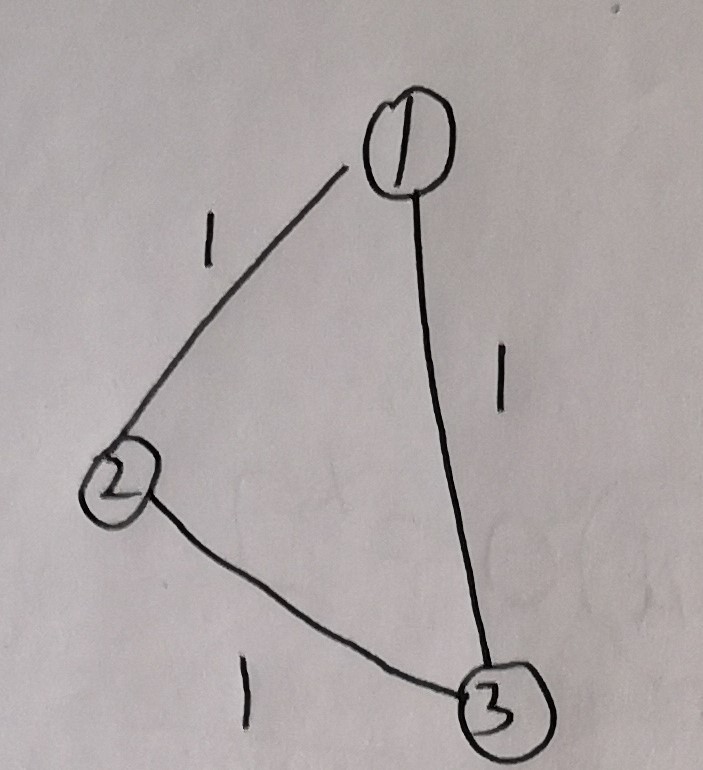
第二步：将4-1-3-5的每两个点的距离设为1：

第三步，合并两路径的图：

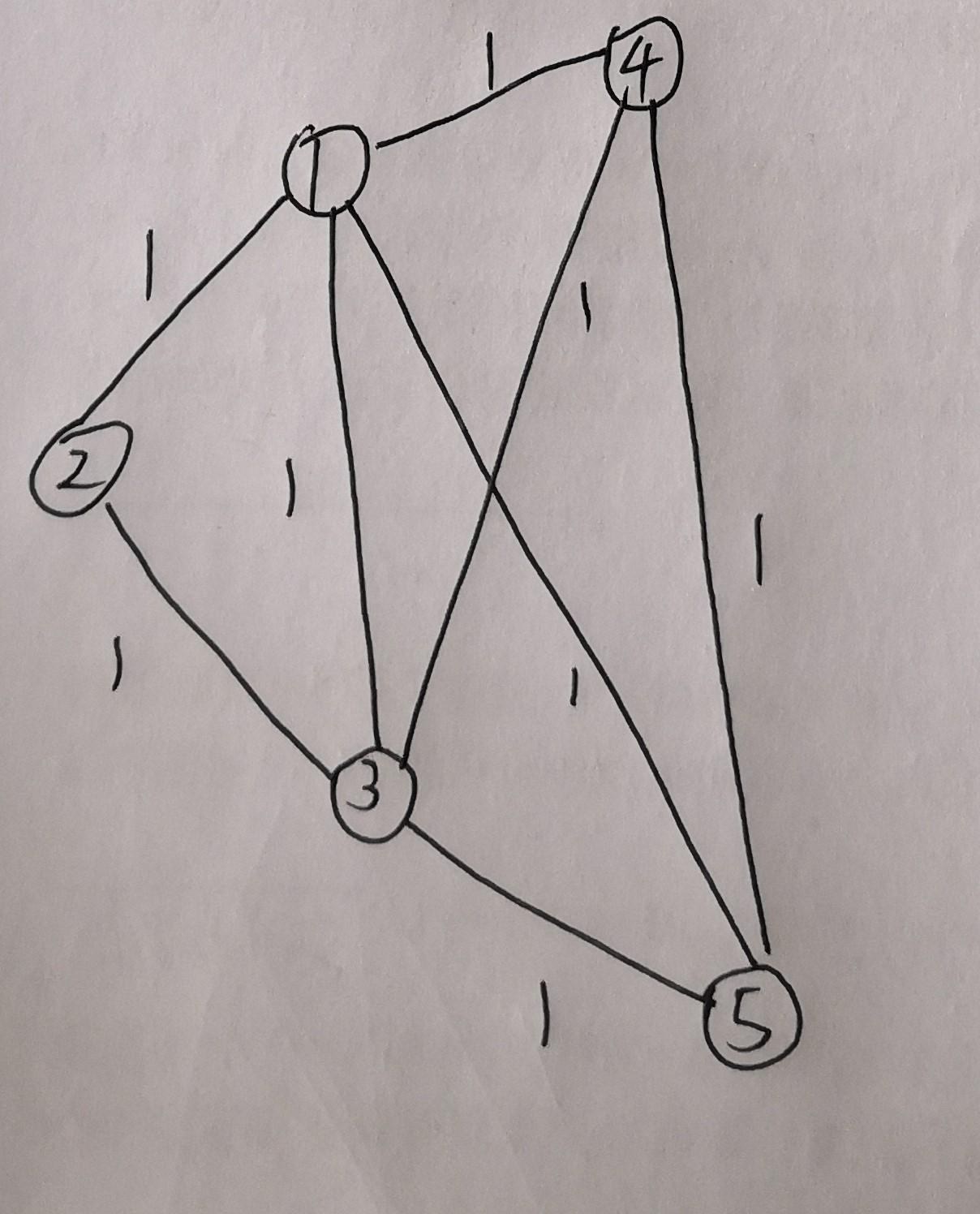
在这个图中计算最少换乘次数就是计算每两个点间的距离再减个1，比如2-3间距离为1，减一就是0，则表示这两个点不需要换乘。2-5距离为2，减一就是1，表示这两个点之间需要换乘1次。

• 对于最低票价，和最少换乘次数想法相仿，就是先将每条路径的每两个点之间的最低票价算出来，将这些值+2后填入矩阵(若有两点间有多条路径，取最低票价)，然后再对整个矩阵进行floyd，每两个点之间的最低票价为对应的矩阵值-2。因为每条路径都可能有环路，所以求每条路径的最短票价时也需要用一次floyd。
• 对于最少不满意度，同最低票价，将每条路径每两个点之间的最少不满意度有用floyd算出来，将这些值+32后填入矩阵(若有两点间有多条路径，取最少不满意度)，然后再对整个矩阵进行floyd，每两个点之间的最少不满意度为对应的矩阵值-32。
• 优化：因为这些矩阵在每一次add或者remove的时候都要更新，如果要把所有路径各自的矩阵全算一遍，然后再把这些矩阵结合起来再算一遍总的最低票价，最少不满意度，这个复杂度会特别高，于是我修改了Path类，将单条路径的不满意度和最低票价存起来，然后设置了一个values类，将每条两个点间的不满意度和最低票价以升序方式存入：

 1 public class Values {
 2     private LinkedList<Integer> valueList = new LinkedList<>();
 3     private static int MAX = 0xfffffff;
 4
 5     public Values() {
 6         valueList.addFirst(MAX);
 7     }
 8
 9
10     public void insert(int e) {
11         for (Integer tmp : valueList) {
12             if (e < tmp) {
13                 valueList.add(valueList.indexOf(tmp),e);
14                 return;
15             }
16         }
17     }
18
19     public int getFirst() {
20         return valueList.getFirst();
21     }
22
23     public void remove(int e) {
24         for (Integer tmp : valueList) {
25             if (e == tmp) {
26                 valueList.remove(tmp);
27                 return;
28             }
29         }
30     }
31 }

连通块数量的计算方法我并没有采用网上说的并查集或者bfs算法，因为经过我的观察，只要有邻接矩阵，就能直接用二重遍历的方式查找出连通块数量，并且速度不比上述两种算法慢：

    public void calConnectNum() {
        int count = 0;
        int[] union = new int[MAXNODE];
        for (int i = 0; i < MAXNODE; i++) {
            if (union[i] > 0) {
                continue;
            }
            boolean flag = false;
            for (int j = i; j < MAXNODE; j++) {
                if (i == j) {
                    if (adjMatrix[i][j] > 0) {
                        union[j] = count + 1;
                        flag = true;
                    }
                }
                else {
                    if (dstMatrix[i][j] < MAXDST) {
                        union[j] = count + 1;
                        flag = true;
                    }
                }
            }
            if (flag) {
                count++;
            }
        }
        connectBlockNum = count;
    }

五、代码分析

---

UML类图：

从左至右分别是第1到3次作业：

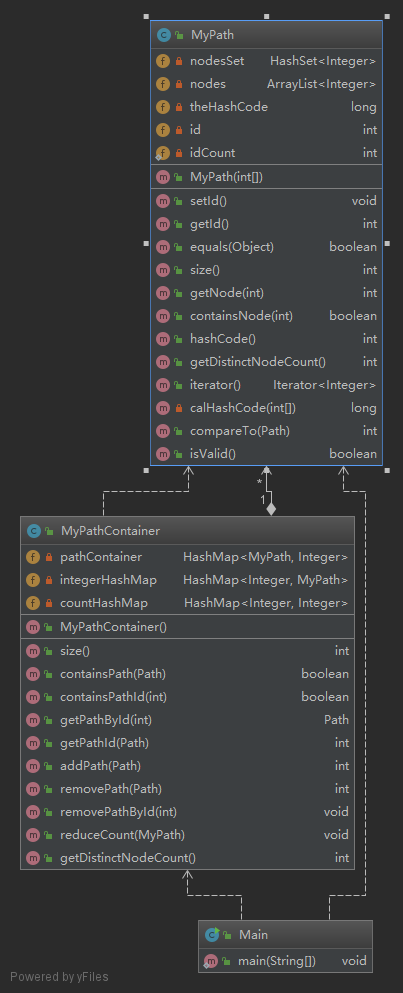
可以看到第一次和第二次依赖关系很简单，第二次只是加了几个方法而已。第三次作业加了一个Values类，增加了一些方法，依赖关系也并不复杂。

代码度量：

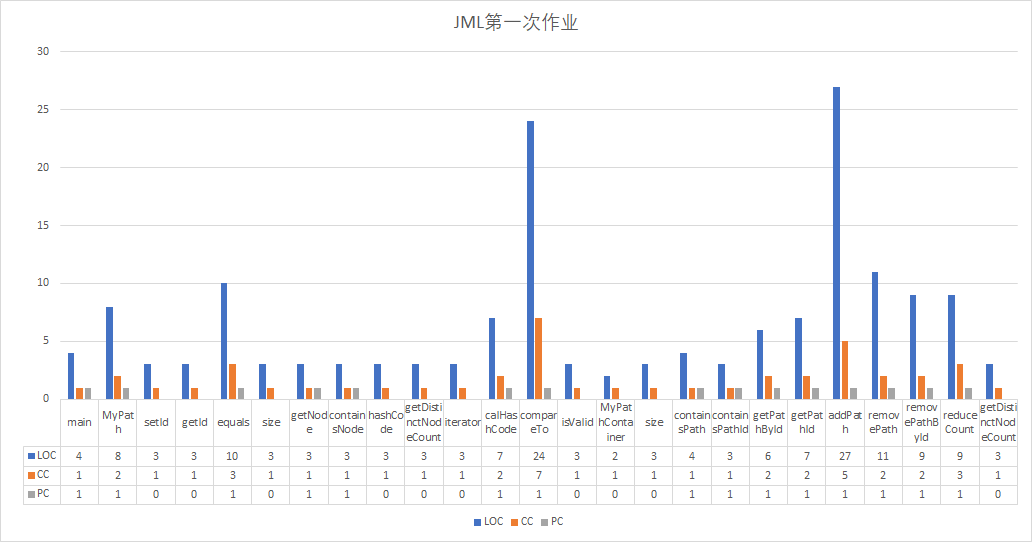
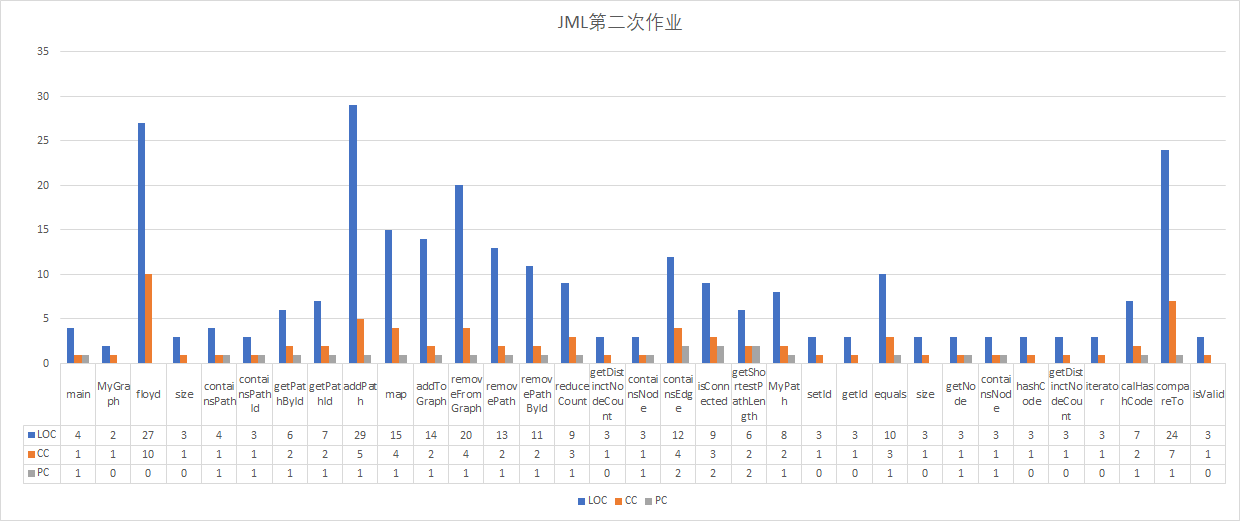
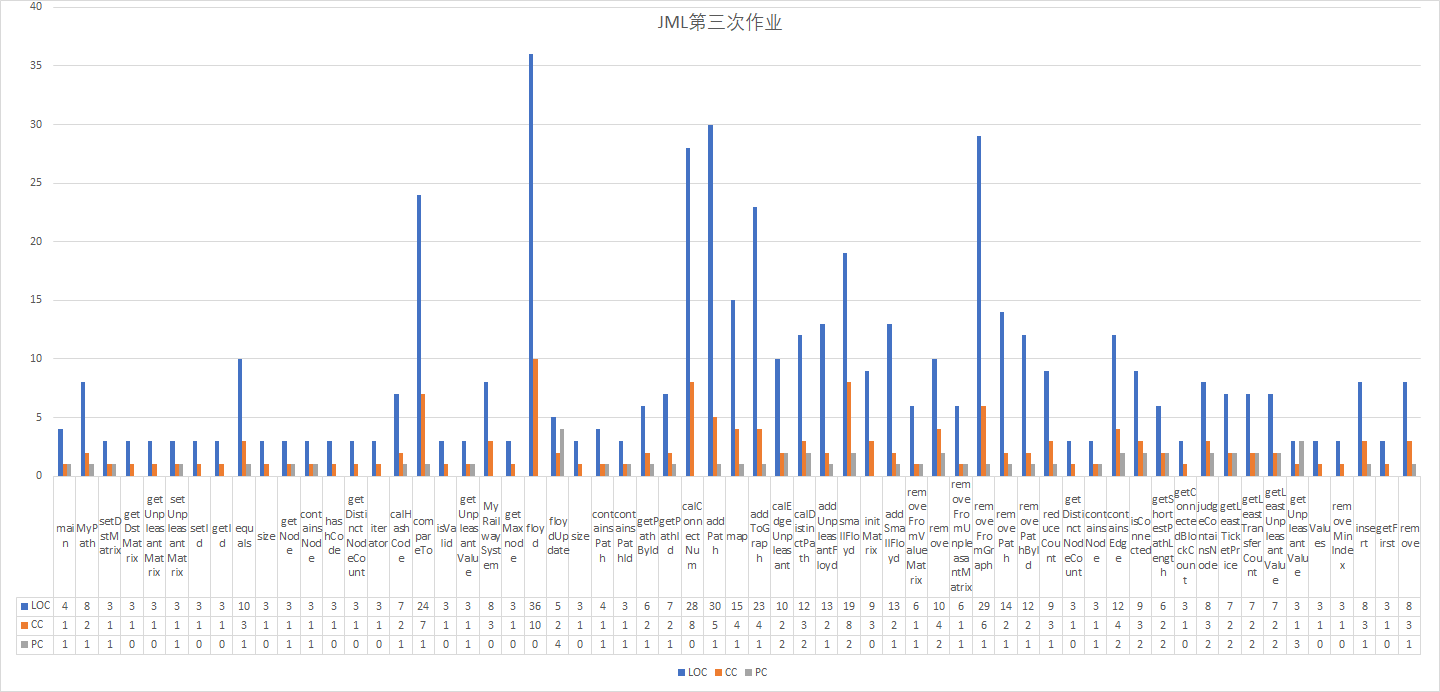
其中：

• LOC (Lines Of Code – at method and class granularity)

  代码行数，可以看到你的方法和类写了多少行。

• CC (Cyclomatic Complexity – Method)

  圈复杂度，用于衡量一个模块判定结构的复杂程度，圈复杂度越大说明程序代码质量低，且难以测试和维护。

• PC (Parameter Count – Method)

  方法中传入的参数个数。

这三次作业的代码量肉眼可见的增加，圈复杂度也从第一次的集中在compareTo到后面floyd等方法，总体来说方法行数平均，没有出现爆方法行数的，圈复杂度除了floyd等少数偏高之外都挺低的，总体来说可以接受。

Bug分析：这三次作业总的来说没有什么BUG，唯一的一个是我在containEdge时忘记先判断点有没有存在图中了，导致数组可能会出现一点点问题，确实时疏忽了。而找BUG我则是写了一个数据生成器，用Random函数随机了很多条指令，然后再去测试他们的程序，然后也用程序生成了一些对时间复杂度要求高的数据来hack别人。

六、学习总结

---

　　本次JML单元让我大开眼界，第一次知道还有契约式编程这种东西，JML规格确实可以让程序员了解需求，然后写出符合规范的代码，只要不脱离规格，程序员就可以自由发挥，爱用什么用什么，在团队协作中确实是一个很不错的工具，但是实际运用中可能还是会受限制，首先 撰写JML语言就是一件很复杂的事，有撰写JML的时间早就把代码写完了，其次openJML不够完善，很多符合规范的代码不被识别，最后JML的社区支持太少，很多问题无法第一时间解决。Junit也是新的工具，以前我们想测试一个方法，要手写一个Main方法，然后把这个方法放进去测试，有了Junit一键生成测试方法，妈妈再也不用担心我的测试了~

　　不过我还是有很大的不足，本次作业可以使用继承与封装使得代码简洁易懂，而我却担心会影响我程序的直观性，怕用了会出现BUG，而没有使用这些面向对象的特性，这是我以后要改正的。

　　总的来说这些工具确实能帮助我们写代码，减少代码BUG 。这三次作业靠着JML和Junit我们完成了如此复杂的一个图论工程，通过这三次作业，我复习了数据结构，更学会了使用新的工具——JML、Junit。