B-tree解释

1 .B-树定义

B-树是一种平衡的多路查找树，它在文件系统中很有用。

定义：一棵m 阶的B-树，或者为空树，或为满足下列特性的m 叉树：
⑴树中每个结点至多有m 棵子树；
⑵若根结点不是叶子结点，则至少有两棵子树；

⑶除根结点之外的所有非终端结点至少有[m/2] 棵子树；
⑷所有的非终端结点中包含以下信息数据：

（n，A0，K1，A1，K2，…，Kn，An）
其中：Ki（i=1,2,…,n）为关键码，且Ki<Ki+1，

 Ai 为指向子树根结点的指针(i=0,1,…,n)，且指针Ai-1 所指子树中所有结点的关键码均小于Ki (i=1,2,…,n)，An 所指子树中所有结点的关键码均大于Kn.

n 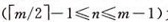  为关键码的个数。
⑸所有的叶子结点都出现在同一层次上，并且不带信息（可以看作是外部结点或查找失败的结点，实际上这些结点不存在，指向这些结点的指针为空）。

即所有叶节点具有相同的深度，等于树高度。

如一棵四阶B-树，其深度为4.

 

 

 

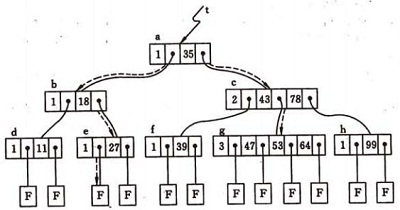
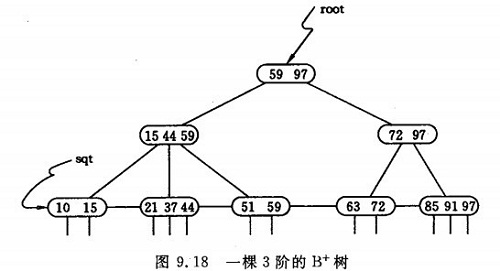
B+树

B+树是应文件系统所需而产生的一种B-树的变形树。一棵m 阶的B+树和m 阶的B-
树的差异在于：
⑴有n 棵子树的结点中含有n 个关键码；
⑵所有的叶子结点中包含了全部关键码的信息，及指向含有这些关键码记录的指针，且
叶子结点本身依关键码的大小自小而大的顺序链接。
⑶所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键码。

 如图一棵3阶的B+树: