牛顿迭代法实现平方根函数sqrt

转自利用牛顿迭代法自己写平方根函数sqrt

给定一个正数a，不用库函数求其平方根。

设其平方根为x，则有x²=a，即x²-a=0。设函数f(x)= x²-a,则可得图示红色的函数曲线。在曲线上任取一点(x₀,f(x₀))，其中x₀≠0那么曲线上该点的切线方程为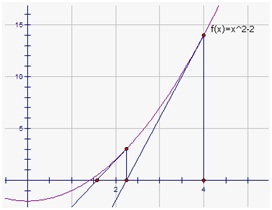

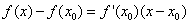     (1-1)

求该切线与x轴的交点得

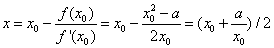     （1-2）

因为1-2式中x₀作为分母，所以在之前限定了一下初始值不要选0。那么得到的这个与x轴的交点其实是最终要求得的x的一次逼近，我们再以这个x基准继续迭代就可以求得更逼近的x，至于逼近到什么时候才算完，这个取决于你自己设定的精度。整个过程的迭代只需要几步就可以求得最终的结果。

代码如下：

[cpp] view
plaincopy

1. double NewtonMethod(double fToBeSqrted)
2. {
3. double x = 1.0;
4. while(abs(x*x-fToBeSqrted) > 1e-5)
5. {
6. x = (x+fToBeSqrted/x)/2;
7. }
8. return x;
9. }

当然，从图中可以看出，当你所取的初始值的横坐标在红色曲线与x轴交点右边，即比最终的结果大时，比如选初始值x=a，我们可以将while语句里面的abs(x*x-fToBeSqrted)直接换成fToBeSqrted -x*x，这样可以省去abs的运算。当然这不能确保效率的提升，因为初始值的选取直接影响了迭代的次数。