约瑟夫问题(Josephus Problem)的两种快速递归算法

• 博文链接：http://haoyuanliu.github.io/2016/04/18/Josephus/
• 对，我是来骗访问量的！O(∩_∩)O~~

---

约瑟夫问题（Josephus Problem）也称“丢手绢问题”，是一道非常经典的算法问题，其解法涉及了链表、递归等算法和数据结构，本文主要分为如下三个内容：

• 使用C语言定义循环链表，通过遍历链表模拟事件处理过程；
• 使用数学方法，找出第n - 1步与第n步的关系，通过递归解决问题；
• 对第二种方法进行优化，加速递归过程，提高算法效率

循环链表（C语言）

代码

#include <stdio.h>
#include <stdlib.h>
//定义循环链表
typedef struct node//定义node结构体
{
    int data;
    struct node* next;
}cLinkList;//typedef struct node* cLinkList;定义一个struct node类型的循环链表

//主函数
int main()
{
    cLinkList *head, *p, *s, *temp;
    int n, k;
    int i = 1;
    printf("Please enter the total number n:\n");
    scanf("%d", &n);
    printf("Please enter the key value:\n");
    scanf("%d", &k);
    k %= n;
    head = (cLinkList *)malloc(sizeof(cLinkList));
    p = head;
    p->next = p;//这里要赋值为p，不能赋值为head，要保持head的位置不变
    p->data = i;
    for(i = 2; i <= n; i++)
    {
        s = (cLinkList *)malloc(sizeof(cLinkList));
        s->data = i;
        s->next = p->next;
        p->next = s;
        p = s;
    }

    p = head;
    int total = n;
    while(n--)
    {
        for(i = 1; i < k - 1; i++)
        {
            p = p->next;
        }
        printf("%d->", p->next->data);
        temp = p->next;//temp为要删除的元素
        p->next = temp->next;//链表中跳过temp
        free(temp);//释放temp
        p = p->next;//p向前移动继续寻找
    }
    printf("Done！\n");
    return 0;
}

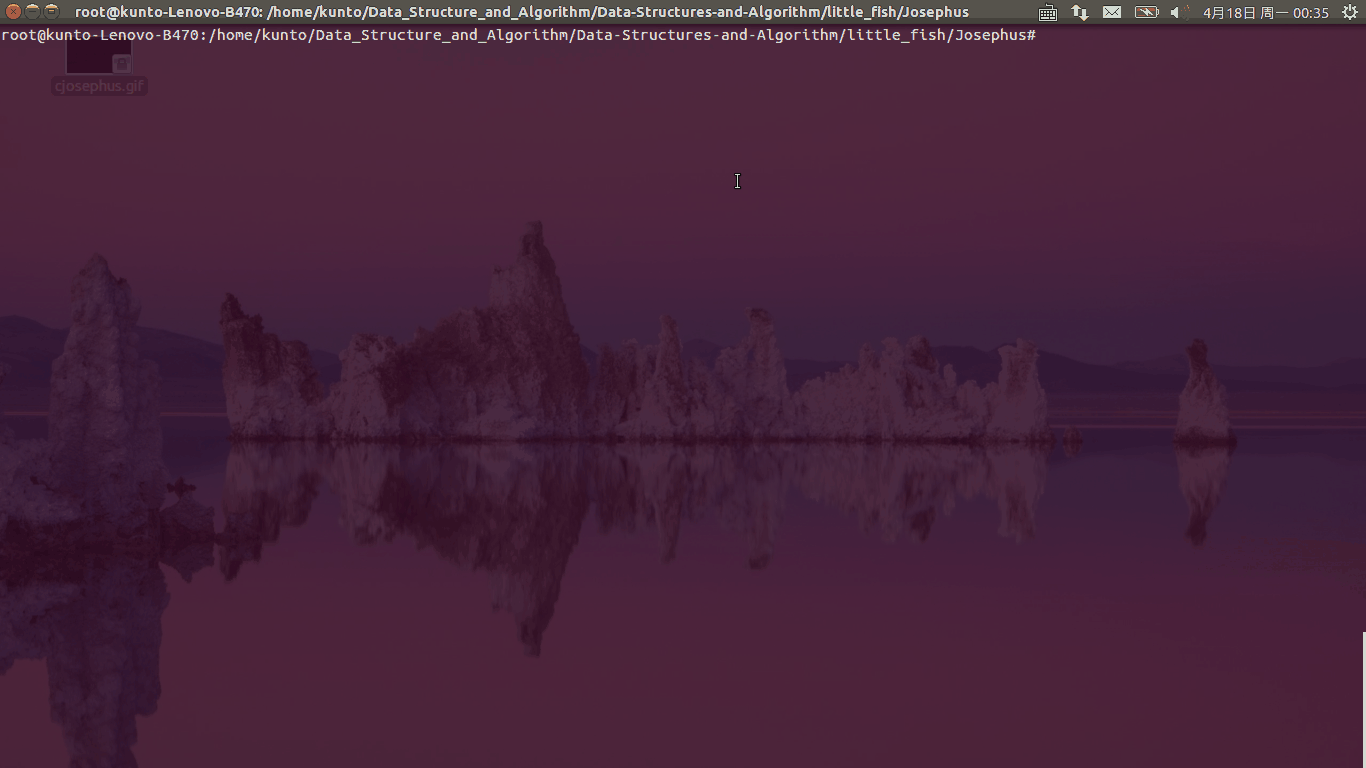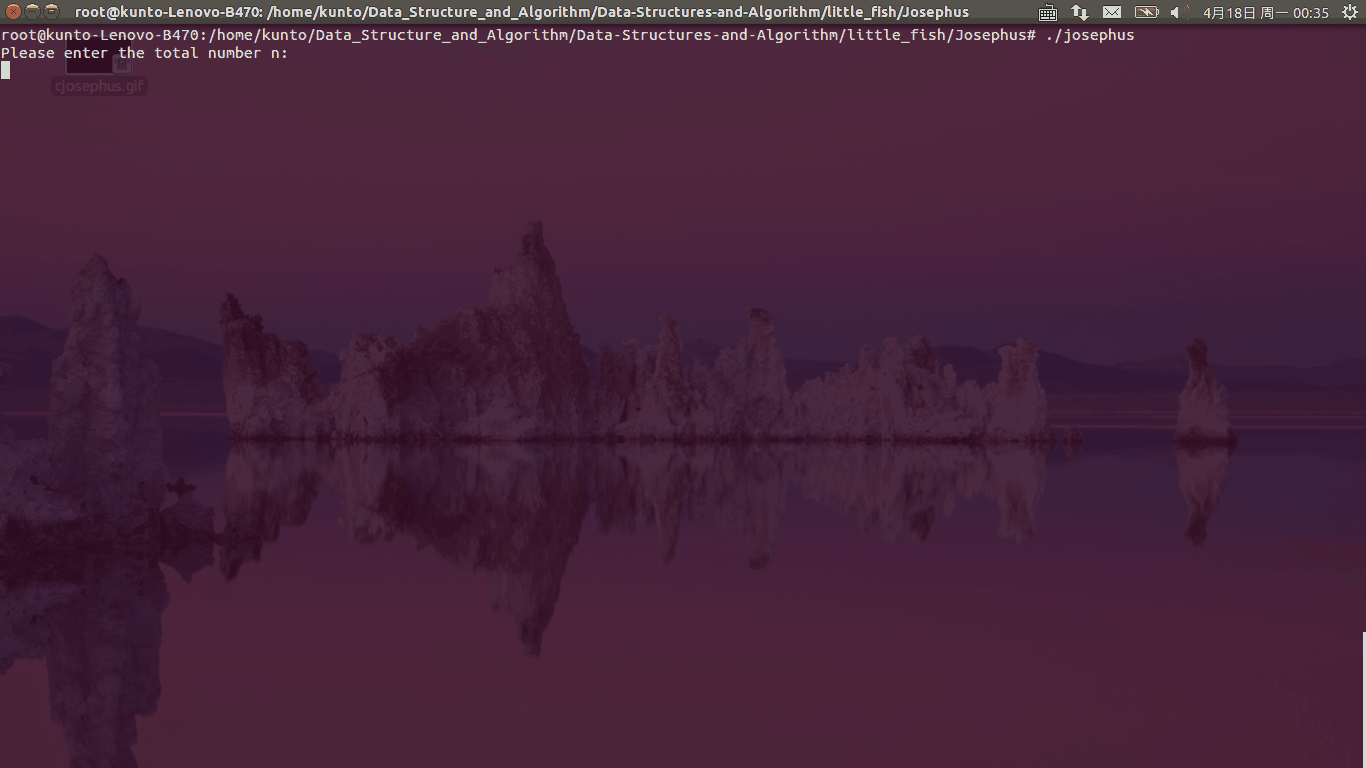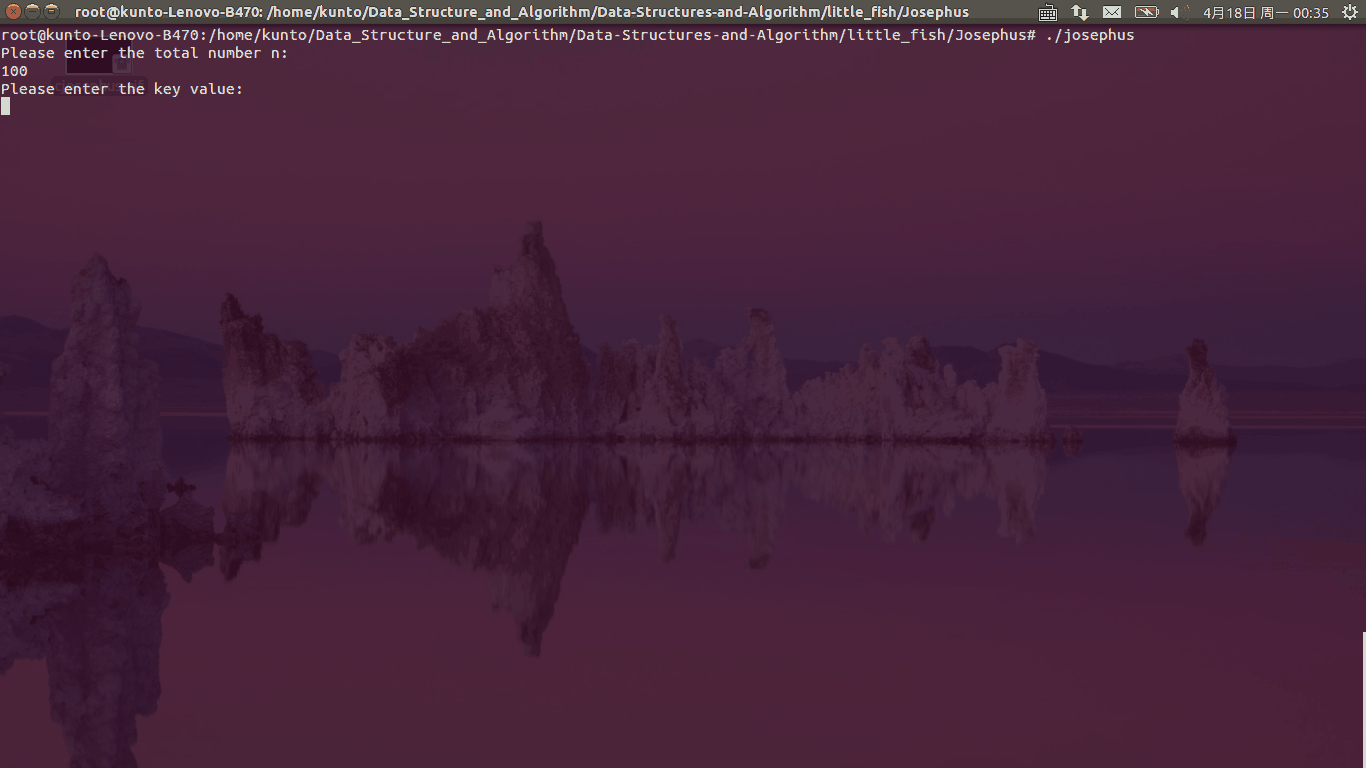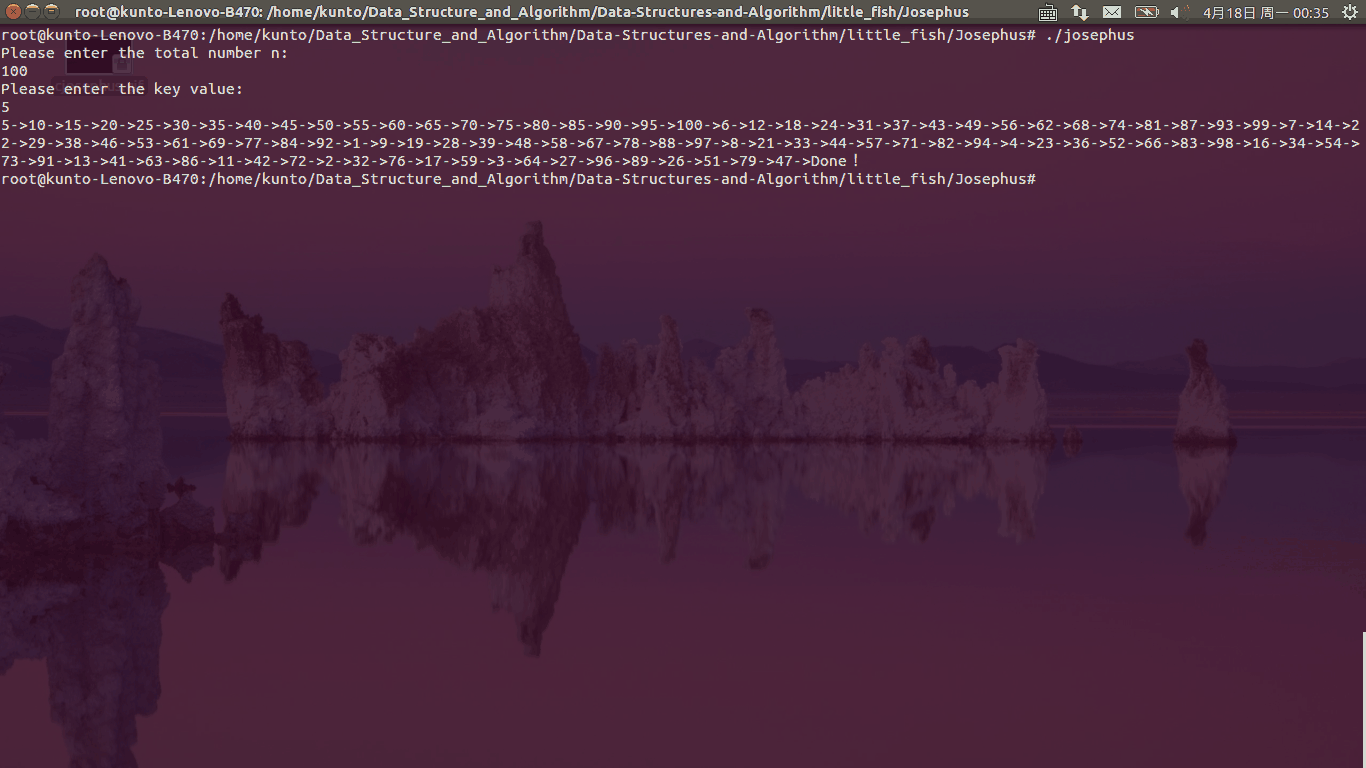
运行过程如下：

程序分析

这段代码主要使用了循环链表的数据特性和结构特性，非常适合用来进行Josephus问题的模拟，但是相对来说处理问题的复杂度较高，下面将介绍两种更加高效的算法。

第一种递归

原理

令f[n]表示当有n个候选人时，最后当选者的编号。则：

f[1] = 0

f[n] = (f[n - 1] + K) mod n

方法证明

上述公式可以用数据归纳法简单证明其正确性：

• f[1] = 0
  
  当只有一个候选人的时候，显然结果应该是0

• f[n] = (f[n - 1] + K) mod n

f[n - 1]为第n - 1次数到的id序列，则第n次就是再往下数k个，最后进行取模运算即可得到结果序列

这种算法的时间复杂度为O(N)，空间复杂度为O(1)，效率有所提高！

代码

#include <iostream>
using namespace std;
int main()
{
    int num, n, k;
    cin >> num;
    while(num--)
    {
        int ret = 0;
        cin >> n >> k;
        for(int i = 2; i <= n; ++i)
        {
            ret = (ret + k) % i;//ret记录每一次数到的序列号
        }
        cout << ret << endl;//输出最终序列结果
    }
    return 0;
}

第二种递归

原理

• 在每一轮报数过程中，都有N/K个人退出了队伍，比如N = 10， K = 3，第一轮有N / K = 3三个人退出；
• 上述第一种方法每次递归的步长为1，这里我们利用上述关系，建立一个步长为N / K的递归过程；
• 需要注意的是，当N减少到N = K的时候就需要使用第一种递归进行计算；
• N > K时的递归公式为：
  
  ret < N mod K: ret = ret - (N mod K) + N

ret >= N mod K: ret = ret - (N mod K) + (ret - N mod K) / (K - 1)

代码

#include <iostream>
using namespace std;
int josephus(int n, int k)
{
    int ret;
    if(n == 1)
        return 0;
    //n < k的时候使用第一种递归算法
    if(n < k)
    {
        int ret = 0;
        for(int i = 2; i <= n; ++i)
            ret = (ret + k) % i;
        return ret;
    }
    //执行递归过程
    ret = josephus(n-n/k,k);
    if(ret < n % k)
    {
        ret = ret - n % k + n;
    }
    else
    {
        ret = ret - n % k + (ret - n % k ) / (k - 1);
    }
    return ret;
}
int main()
{
    int num;
    cin >> num;
    while(num--)
    {
        int n, k;
        cin >> n >> k;
        cout << josephus(n, k) << endl;
    }
    return 0;
}

代码分析

这个算法加快了递归算法的迭代速度，当所求N比较大K比较小的时候比较适用，能够以更快的速度进行求解。

---

---

Github： https://github.com/haoyuanliu

个人博客： http://haoyuanliu.github.io/

个人站点，欢迎访问，欢迎评论！