支持向量机(SVM)——python3实现

　　今天看完soft-margin SVM就又搜了下相关的代码，最后搜到这个，第一次看懂了SVM的实现。

　　关于代码中cvxopt的使用，可以看下这个简单的介绍。

　　这里还是将代码贴在这里，里面加了自己的一下注释。

 # -*- coding: utf-8 -*-
 """
 Created on Tue Nov 22 11:24:22 2016

 @author: Administrator
 """

 # Mathieu Blondel, September 2010
 # License: BSD 3 clause

 import numpy as np
 from numpy import linalg
 import cvxopt
 import cvxopt.solvers

 def linear_kernel(x1, x2):
     return np.dot(x1, x2)

 def polynomial_kernel(x, y, p=3):
     return (1 + np.dot(x, y)) ** p

 def gaussian_kernel(x, y, sigma=5.0):
     return np.exp(-linalg.norm(x-y)**2 / (2 * (sigma ** 2)))

 class SVM(object):

     def __init__(self, kernel=linear_kernel, C=None):
         self.kernel = kernel
         self.C = C
         if self.C is not None: self.C = float(self.C)

     def fit(self, X, y):
         n_samples, n_features = X.shape

         # Gram matrix
         K = np.zeros((n_samples, n_samples))
         for i in range(n_samples):
             for j in range(n_samples):
                 K[i,j] = self.kernel(X[i], X[j])

         P = cvxopt.matrix(np.outer(y,y) * K)
         q = cvxopt.matrix(np.ones(n_samples) * -1)
         A = cvxopt.matrix(y, (1,n_samples))
         b = cvxopt.matrix(0.0)

         if self.C is None:
             G = cvxopt.matrix(np.diag(np.ones(n_samples) * -1))
             h = cvxopt.matrix(np.zeros(n_samples))
         else:
             tmp1 = np.diag(np.ones(n_samples) * -1)
             tmp2 = np.identity(n_samples)
             G = cvxopt.matrix(np.vstack((tmp1, tmp2)))
             tmp1 = np.zeros(n_samples)
             tmp2 = np.ones(n_samples) * self.C
             h = cvxopt.matrix(np.hstack((tmp1, tmp2)))

         # solve QP problem
         solution = cvxopt.solvers.qp(P, q, G, h, A, b)
         # Lagrange multipliers
         '''
          数组的flatten和ravel方法将数组变为一个一维向量（铺平数组）。
          flatten方法总是返回一个拷贝后的副本，
          而ravel方法只有当有必要时才返回一个拷贝后的副本（所以该方法要快得多，尤其是在大数组上进行操作时）
        '''
         a = np.ravel(solution['x'])
         # Support vectors have non zero lagrange multipliers
         '''
         这里a>1e-5就将其视为非零
         '''
         sv = a > 1e-5     # return a list with bool values
         ind = np.arange(len(a))[sv]  # sv's index
         self.a = a[sv]
         self.sv = X[sv]  # sv's data
         self.sv_y = y[sv]  # sv's labels
         print("%d support vectors out of %d points" % (len(self.a), n_samples))

         # Intercept
         '''
         这里相当于对所有的支持向量求得的b取平均值
         '''
         self.b = 0
         for n in range(len(self.a)):
             self.b += self.sv_y[n]
             self.b -= np.sum(self.a * self.sv_y * K[ind[n],sv])
         self.b /= len(self.a)

         # Weight vector
         if self.kernel == linear_kernel:
             self.w = np.zeros(n_features)
             for n in range(len(self.a)):
                 # linear_kernel相当于在原空间，故计算w不用映射到feature space
                 self.w += self.a[n] * self.sv_y[n] * self.sv[n]
         else:
             self.w = None

     def project(self, X):
         # w有值，即kernel function 是 linear_kernel，直接计算即可
         if self.w is not None:
             return np.dot(X, self.w) + self.b
         # w is None --> 不是linear_kernel,w要重新计算
         # 这里没有去计算新的w（非线性情况不用计算w）,直接用kernel matrix计算预测结果
         else:
             y_predict = np.zeros(len(X))
             for i in range(len(X)):
                 s = 0
                 for a, sv_y, sv in zip(self.a, self.sv_y, self.sv):
                     s += a * sv_y * self.kernel(X[i], sv)
                 y_predict[i] = s
             return y_predict + self.b

     def predict(self, X):
         return np.sign(self.project(X))

 if __name__ == "__main__":
     import pylab as pl

     def gen_lin_separable_data():
         # generate training data in the 2-d case
         mean1 = np.array([0, 2])
         mean2 = np.array([2, 0])
         cov = np.array([[0.8, 0.6], [0.6, 0.8]])
         X1 = np.random.multivariate_normal(mean1, cov, 100)
         y1 = np.ones(len(X1))
         X2 = np.random.multivariate_normal(mean2, cov, 100)
         y2 = np.ones(len(X2)) * -1
         return X1, y1, X2, y2

     def gen_non_lin_separable_data():
         mean1 = [-1, 2]
         mean2 = [1, -1]
         mean3 = [4, -4]
         mean4 = [-4, 4]
         cov = [[1.0,0.8], [0.8, 1.0]]
         X1 = np.random.multivariate_normal(mean1, cov, 50)
         X1 = np.vstack((X1, np.random.multivariate_normal(mean3, cov, 50)))
         y1 = np.ones(len(X1))
         X2 = np.random.multivariate_normal(mean2, cov, 50)
         X2 = np.vstack((X2, np.random.multivariate_normal(mean4, cov, 50)))
         y2 = np.ones(len(X2)) * -1
         return X1, y1, X2, y2

     def gen_lin_separable_overlap_data():
         # generate training data in the 2-d case
         mean1 = np.array([0, 2])
         mean2 = np.array([2, 0])
         cov = np.array([[1.5, 1.0], [1.0, 1.5]])
         X1 = np.random.multivariate_normal(mean1, cov, 100)
         y1 = np.ones(len(X1))
         X2 = np.random.multivariate_normal(mean2, cov, 100)
         y2 = np.ones(len(X2)) * -1
         return X1, y1, X2, y2

     def split_train(X1, y1, X2, y2):
         X1_train = X1[:90]
         y1_train = y1[:90]
         X2_train = X2[:90]
         y2_train = y2[:90]
         X_train = np.vstack((X1_train, X2_train))
         y_train = np.hstack((y1_train, y2_train))
         return X_train, y_train

     def split_test(X1, y1, X2, y2):
         X1_test = X1[90:]
         y1_test = y1[90:]
         X2_test = X2[90:]
         y2_test = y2[90:]
         X_test = np.vstack((X1_test, X2_test))
         y_test = np.hstack((y1_test, y2_test))
         return X_test, y_test

     # 仅仅在Linears使用此函数作图，即w存在时
     def plot_margin(X1_train, X2_train, clf):
         def f(x, w, b, c=0):
             # given x, return y such that [x,y] in on the line
             # w.x + b = c
             return (-w[0] * x - b + c) / w[1]

         pl.plot(X1_train[:,0], X1_train[:,1], "ro")
         pl.plot(X2_train[:,0], X2_train[:,1], "bo")
         pl.scatter(clf.sv[:,0], clf.sv[:,1], s=100, c="g")

         # w.x + b = 0
         a0 = -4; a1 = f(a0, clf.w, clf.b)
         b0 = 4; b1 = f(b0, clf.w, clf.b)
         pl.plot([a0,b0], [a1,b1], "k")

         # w.x + b = 1
         a0 = -4; a1 = f(a0, clf.w, clf.b, 1)
         b0 = 4; b1 = f(b0, clf.w, clf.b, 1)
         pl.plot([a0,b0], [a1,b1], "k--")

         # w.x + b = -1
         a0 = -4; a1 = f(a0, clf.w, clf.b, -1)
         b0 = 4; b1 = f(b0, clf.w, clf.b, -1)
         pl.plot([a0,b0], [a1,b1], "k--")

         pl.axis("tight")
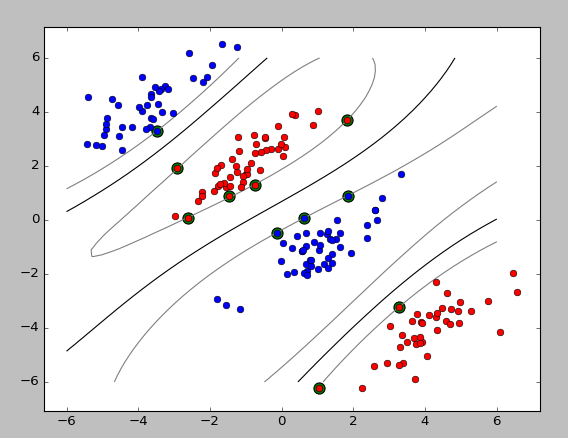
         pl.show()

     def plot_contour(X1_train, X2_train, clf):
         # 作training sample数据点的图
         pl.plot(X1_train[:,0], X1_train[:,1], "ro")
         pl.plot(X2_train[:,0], X2_train[:,1], "bo")
         # 做support vectors 的图
         pl.scatter(clf.sv[:,0], clf.sv[:,1], s=100, c="g")
         X1, X2 = np.meshgrid(np.linspace(-6,6,50), np.linspace(-6,6,50))
         X = np.array([[x1, x2] for x1, x2 in zip(np.ravel(X1), np.ravel(X2))])
         Z = clf.project(X).reshape(X1.shape)
         # pl.contour做等值线图
         pl.contour(X1, X2, Z, [0.0], colors='k', linewidths=1, origin='lower')
         pl.contour(X1, X2, Z + 1, [0.0], colors='grey', linewidths=1, origin='lower')
         pl.contour(X1, X2, Z - 1, [0.0], colors='grey', linewidths=1, origin='lower')

         pl.axis("tight")
         pl.show()

     def test_linear():
         X1, y1, X2, y2 = gen_lin_separable_data()
         X_train, y_train = split_train(X1, y1, X2, y2)
         X_test, y_test = split_test(X1, y1, X2, y2)

         clf = SVM()
         clf.fit(X_train, y_train)

         y_predict = clf.predict(X_test)
         correct = np.sum(y_predict == y_test)
         print("%d out of %d predictions correct" % (correct, len(y_predict)))

         plot_margin(X_train[y_train==1], X_train[y_train==-1], clf)

     def test_non_linear():
         X1, y1, X2, y2 = gen_non_lin_separable_data()
         X_train, y_train = split_train(X1, y1, X2, y2)
         X_test, y_test = split_test(X1, y1, X2, y2)

         clf = SVM(gaussian_kernel)
         clf.fit(X_train, y_train)

         y_predict = clf.predict(X_test)
         correct = np.sum(y_predict == y_test)
         print("%d out of %d predictions correct" % (correct, len(y_predict)))

         plot_contour(X_train[y_train==1], X_train[y_train==-1], clf)

     def test_soft():
         X1, y1, X2, y2 = gen_lin_separable_overlap_data()
         X_train, y_train = split_train(X1, y1, X2, y2)
         X_test, y_test = split_test(X1, y1, X2, y2)

         clf = SVM(C=0.1)
         clf.fit(X_train, y_train)

         y_predict = clf.predict(X_test)
         correct = np.sum(y_predict == y_test)
         print("%d out of %d predictions correct" % (correct, len(y_predict)))

         plot_contour(X_train[y_train==1], X_train[y_train==-1], clf)

     # test_soft()
     # test_linear()
     test_non_linear()

　　运行结果：