从图(Graph)到图卷积(Graph Convolution)：漫谈图神经网络模型 (二)

本文属于图神经网络的系列文章，文章目录如下：

• 从图(Graph)到图卷积(Graph Convolution)：漫谈图神经网络模型 (一)
• 从图(Graph)到图卷积(Graph Convolution)：漫谈图神经网络模型 (二)
• 从图(Graph)到图卷积(Graph Convolution)：漫谈图神经网络模型 (三)

---

在上一篇博客中，我们简单介绍了基于循环图神经网络的两种重要模型，在本篇中，我们将着大量笔墨介绍图卷积神经网络中的卷积操作。接下来，我们将首先介绍一下图卷积神经网络的大概框架，借此说明它与基于循环的图神经网络的区别。接着，我们将从头开始为读者介绍卷积的基本概念，以及其在物理模型中的涵义。最后，我们将详细地介绍两种不同的卷积操作，分别为空域卷积和时域卷积，与其对应的经典模型。读者不需有任何信号处理方面的基础，傅里叶变换等概念都会在本文中详细介绍。

图卷积缘起

在开始正式介绍图卷积之前，我们先花一点篇幅探讨一个问题：为什么研究者们要设计图卷积操作，传统的卷积不能直接用在图上吗？ 要理解这个问题，我们首先要理解能够应用传统卷积的图像(欧式空间)与图(非欧空间)的区别。如果把图像中的每个像素点视作一个结点，如下图左侧所示，一张图片就可以看作一个非常稠密的图；下图右侧则是一个普通的图。阴影部分代表卷积核，左侧是一个传统的卷积核，右侧则是一个图卷积核。卷积代表的含义我们会在后文详细叙述，这里读者可以将其理解为在局部范围内的特征抽取方法。

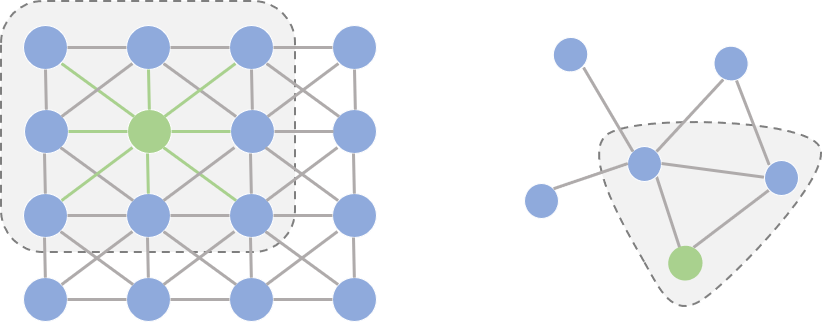
仔细观察两个图的结构，我们可以发现它们之间有2点非常不一样：

• 在图像为代表的欧式空间中，结点的邻居数量都是固定的。比如说绿色结点的邻居始终是8个(边缘上的点可以做Padding填充)。但在图这种非欧空间中，结点有多少邻居并不固定。目前绿色结点的邻居结点有2个，但其他结点也会有5个邻居的情况。
• 欧式空间中的卷积操作实际上是用固定大小可学习的卷积核来抽取像素的特征，比如这里就是抽取绿色结点对应像素及其相邻像素点的特征。但是因为图里的邻居结点不固定，所以传统的卷积核不能直接用于抽取图上结点的特征。

真正的难点聚焦于邻居结点数量不固定上。那么，研究者如何解决这个问题呢？其实说来也很简单，目前主流的研究从2条路来解决这件事：

• 提出一种方式把非欧空间的图转换成欧式空间。
• 找出一种可处理变长邻居结点的卷积核在图上抽取特征。

这两条实际上也是后续图卷积神经网络的设计原则，图卷积的本质是想找到适用于图的可学习卷积核。

图卷积框架(Framework)

上面说了图卷积的核心特征，下面我们先来一窥图卷积神经网络的全貌。如下图所示，输入的是整张图，在Convolution Layer 1里，对每个结点的邻居都进行一次卷积操作，并用卷积的结果更新该结点；然后经过激活函数如ReLU，然后再过一层卷积层Convolution Layer 2与一词激活函数；反复上述过程，直到层数达到预期深度。与GNN类似，图卷积神经网络也有一个局部输出函数，用于将结点的状态(包括隐藏状态与结点特征)转换成任务相关的标签，比如水军账号分类，本文中笔者称这种任务为Node-Level的任务；也有一些任务是对整张图进行分类的，比如化合物分类，本文中笔者称这种任务为Graph-Level的任务。卷积操作关心每个结点的隐藏状态如何更新，而对于Graph-Level的任务，它们会在卷积层后加入更多操作。本篇博客主要关心如何在图上做卷积，至于如何从结点信息得到整张图的表示，我们将在下一篇系列博客中讲述。

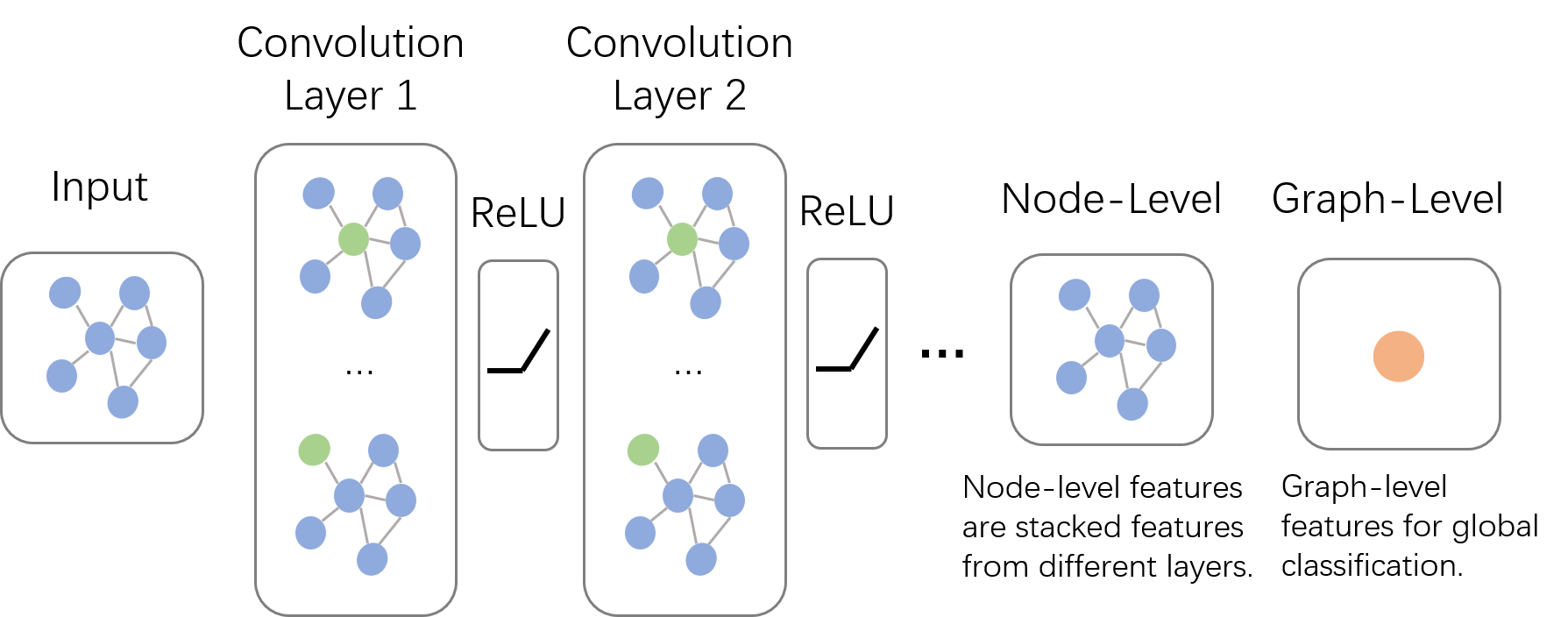
多说一句，GCN与GNN乍看好像还挺像的。为了不让读者误解，在这里我们澄清一下它们根本上的不同：GCN是多层堆叠，比如上图中的Layer 1和Layer 2的参数是不同的；GNN是迭代求解，可以看作每一层Layer参数是共享的。

卷积(Convolution)

正如我们在上篇博客的开头说到的，图卷积神经网络主要有两类，一类是基于空域的，另一类则是基于频域的。通俗点解释，空域可以类比到直接在图片的像素点上进行卷积，而频域可以类比到对图片进行傅里叶变换后，再进行卷积。傅里叶变换的概念我们先按下不讲，我们先对两类方法的代表模型做个大概介绍。

基于空域卷积的方法直接将卷积操作定义在每个结点的连接关系上，它跟传统的卷积神经网络中的卷积更相似一些。在这个类别中比较有代表性的方法有 Message Passing Neural Networks(MPNN)[1], GraphSage[2], Diffusion Convolution Neural Networks(DCNN)[3], PATCHY-SAN[4]等。

基于频域卷积的方法则从图信号处理起家，包括 Spectral CNN[5], Cheybyshev Spectral CNN(ChebNet)[6], 和 First order of ChebNet(1stChebNet)[7]等。

在介绍这些具体的模型前，先让我们从不同的角度来回顾一下卷积的概念，重新思考一下卷积的本质。

基础概念

由维基百科的介绍我们可以得知，卷积是一种定义在两个函数(\(f\)跟\(g\))上的数学操作，旨在产生一个新的函数。那么\(f\)和\(g\)的卷积就可以写成\(f*g\)，数学定义如下：

\[(f*g)(t)={\int}_{-\infty}^{\infty}f(\tau)g(t-\tau) (连续形式)\]
\[(f*g)(t)={\sum}_{\tau=-\infty}^{\infty}f(\tau)g(t-\tau) (离散形式)\]

实例:掷骰子问题

光看数学定义可能会觉得非常抽象，下面我们举一个掷骰子的问题，该实例参考了知乎问题"如何通俗易懂地解释卷积"[8]的回答。

想象我们现在有两个骰子，两个骰子分别是\(f\)跟\(g\)，\(f(1)\)表示骰子\(f\)向上一面为数字\(1\)的概率。同时抛掷这两个骰子1次，它们正面朝上数字和为4的概率是多少呢？相信读者很快就能想出它包含了三种情况，分别是：

• \(f\) 向上为1，\(g\) 向上为3；
• \(f\) 向上为2，\(g\) 向上为2；
• \(f\) 向上为3，\(g\) 向上为1；

最后这三种情况出现的概率和即问题的答案，如果写成公式，就是 \(\sum_{\tau=1}^{3}f(\tau)g(4-\tau)\)。可以形象地绘制成下图：

如果稍微扩展一点，比如说我们认为 \(f(0)\) 或者 \(g(0)\) 等是可以取到的，只是它们的值为0而已。那么该公式可以写成\(\sum_{\tau=-\infty}^{\infty}f(\tau)g(4-\tau)\)。仔细观察，这其实就是卷积\((f*g)(4)\)。如果将它写成内积的形式，卷积其实就是 \([f(-\infty),\cdots,f(1),\cdots,f(\infty)] \cdot [g(\infty),\cdots,g(3),\cdots,g(-\infty)]\)。这么一看，是不是就对卷积的名字理解更深刻了呢? 所谓卷积，其实就是把一个函数卷(翻)过来，然后与另一个函数求内积。

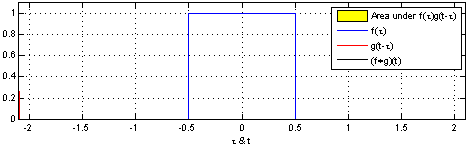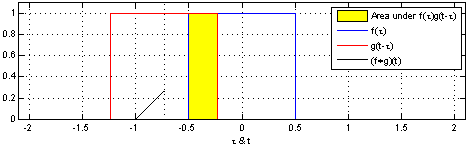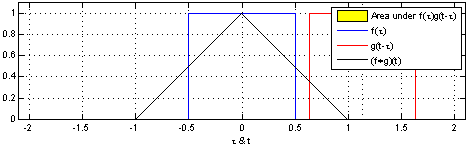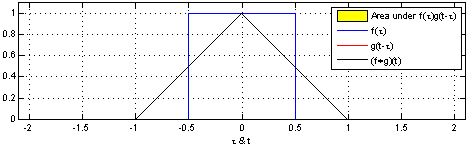
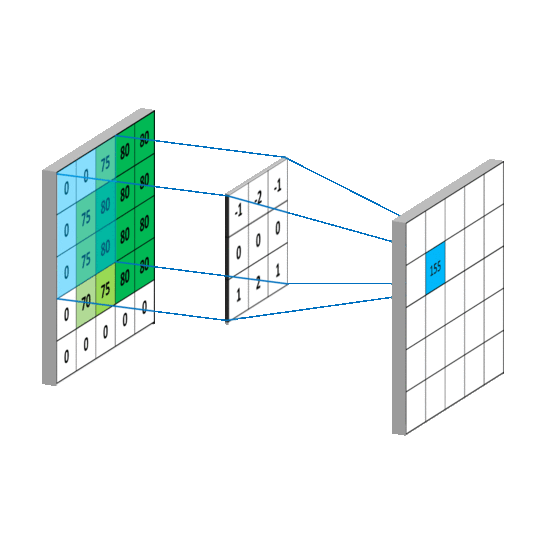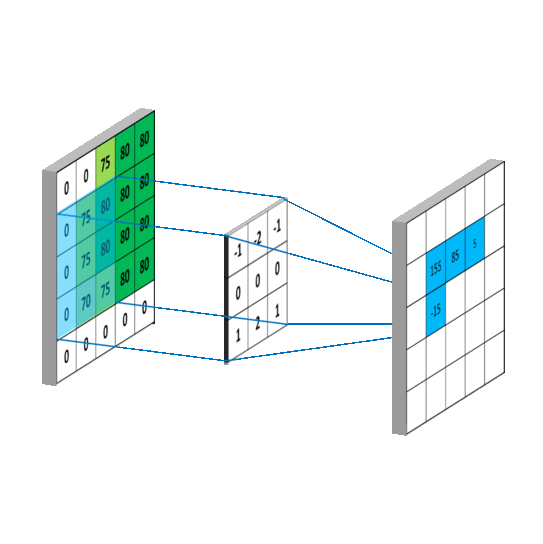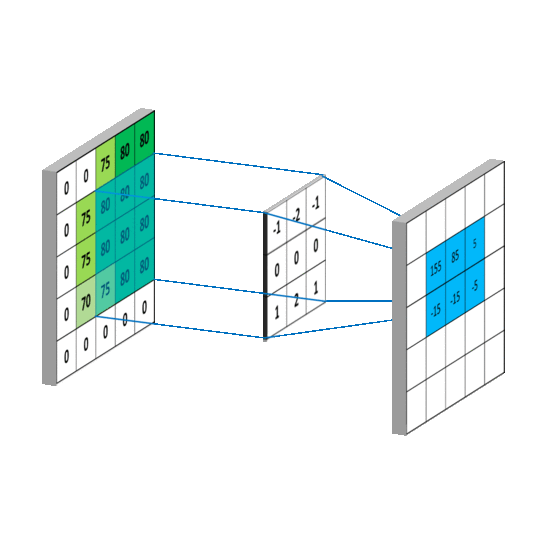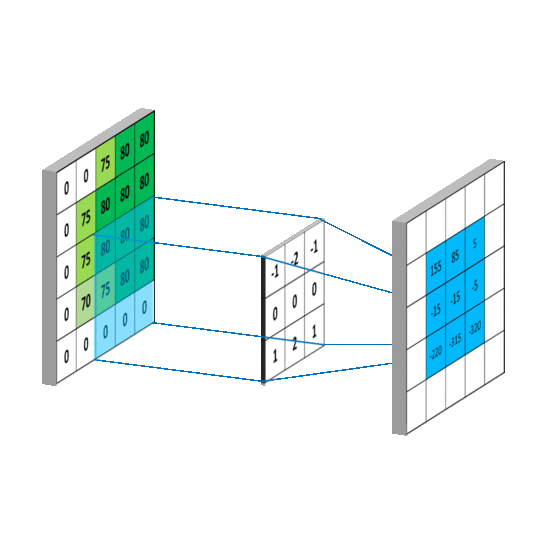
对应到不同方面，卷积可以有不同的解释：\(g\) 既可以看作我们在深度学习里常说的核(Kernel)，也可以对应到信号处理中的滤波器(Filter)。而 \(f\) 可以是我们所说的机器学习中的特征(Feature)，也可以是信号处理中的信号(Signal)。f和g的卷积 \((f*g)\)就可以看作是对\(f\)的加权求和。下面两个动图就分别对应信号处理与深度学习中卷积操作的过程[9][10]。

空域卷积(Spatial Convolution)

介绍完卷积的基础概念后，我们先来介绍下空域卷积(Spatial Convolution)。从设计理念上看，空域卷积与深度学习中的卷积的应用方式类似，其核心在于聚合邻居结点的信息。比如说，一种最简单的无参卷积方式可以是：将所有直连邻居结点的隐藏状态加和，来更新当前结点的隐藏状态。

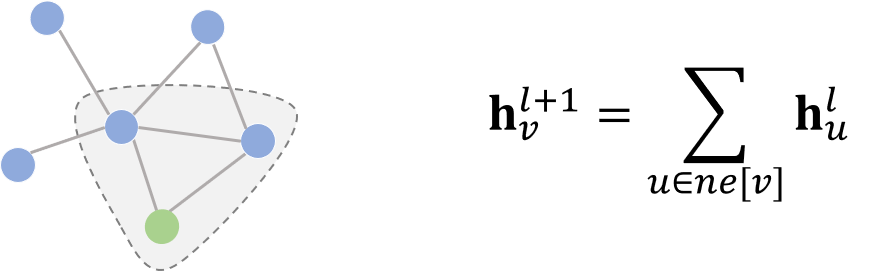
这里非参式的卷积只是为了举一个简单易懂的例子，实际上图卷积在建模时需要的都是带参数、可学习的卷积核。

消息传递网络(Message Passing Neural Network)

消息传递网络(MPNN)[1] 是由Google的科学家提出的一种模型。严格意义上讲，MPNN是一种框架，它将在空域卷积模型统一成两个过程：消息传递与状态更新操作，分别由\(M_{l}(\cdot)\)和\(U_{l}(\cdot)\)函数完成。将结点\(v\)的特征\(\mathbf{x}_v\)作为其隐藏状态的初始态\(\mathbf{h}_{v}^0\)后，状态更新可以由如下公式表示：

\[\mathbf{h}_{v}^{l+1}=U_{l+1}(\mathbf{h}_v,\sum_{u{\in}ne[v]}M_{l+1}(\mathbf{h}_v^l,\mathbf{h}_u^l,\mathbf{x}_{vu}))\]

其中\(l\)代表图卷积的第\(l\)层，上式的物理意义是：收到来自邻居的消息\(M\)后，图中的每个结点状态更新的方式。

如果读者还记得GGNN的话，可能会觉得这个公式与GGNN的公式很像。实际上，它们是截然不同的两种方式：GCN中通过级联的层捕捉邻居的消息，GNN通过级联的时间来捕捉邻居的消息；前者层与层之间的参数不同，后者可以视作层与层之间共享参数。MPNN的示意图如下[11]：

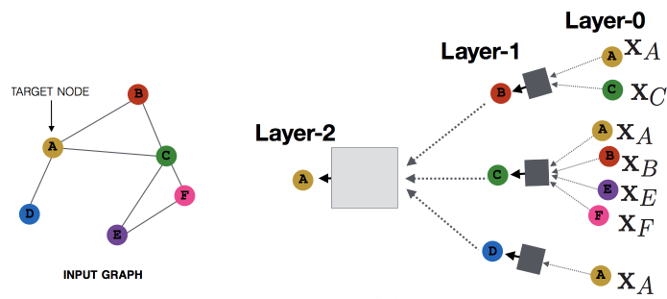
图采样与聚合(Graph Sample and Aggregate)

MPNN很好地概括了空域卷积的基本模型，但它每次训练时都必须将整个图作为输入，这对很多实际场景来说是不现实的。GraphSage[2]提出的动机之一就是解决这个问题，从它的名字也能看出来，它只需要采样(Sample)就可以学习，而不需要将整张图作为输入。虽然不再需要整张图同时输入，GraphSage仍然需要聚合邻居结点的信息，它定义了aggregate的操作，类似于MPNN中的消息传递。最终，GraphSage的状态更新公式如下：

\[\mathbf{h}_{v}^{l+1}=\sigma(\mathbf{W}^{l+1}(\mathbf{h}_v^l,\{\mathbf{h}_u^l\}),{\forall}u{\in}ne[v])\]

频域卷积(Spectral Convolution)

参考文献

[1]. Neural Message Passing for Quantum Chemistry, https://arxiv.org/abs/1704.01212

[2]. Inductive Representation Learning on Large Graphs, https://arxiv.org/abs/1706.02216

[3]. Diffusion-Convolutional Neural Networks, https://arxiv.org/abs/1511.02136

[4]. Learning Convolutional Neural Networks for Graphs, https://arxiv.org/pdf/1605.05273

[5].

[6].

[7].

[8]. 如何通俗易懂地解释卷积, https://www.zhihu.com/question/22298352

[9]. https://en.wikipedia.org/wiki/Convolution

[10]. https://mlnotebook.github.io/post/CNN1/

[11]. http://snap.stanford.edu/proj/embeddings-www