Crash的数字表格 BZOJ 2154 / jzptab BZOJ 2693

jzptab

【问题描述】

求：

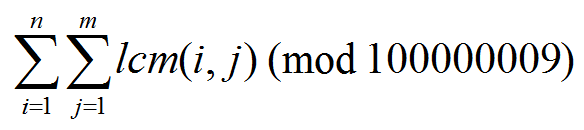
多组询问

【输入格式】

一个正整数T表示数据组数

接下来T行 每行两个正整数 表示N、M

【输出格式】

T行 每行一个整数 表示第i组数据的结果

【样例输入】

1
4 5

【样例输出】

122

【数据范围】

T <= 10000
N, M<=10000000

---

题解：

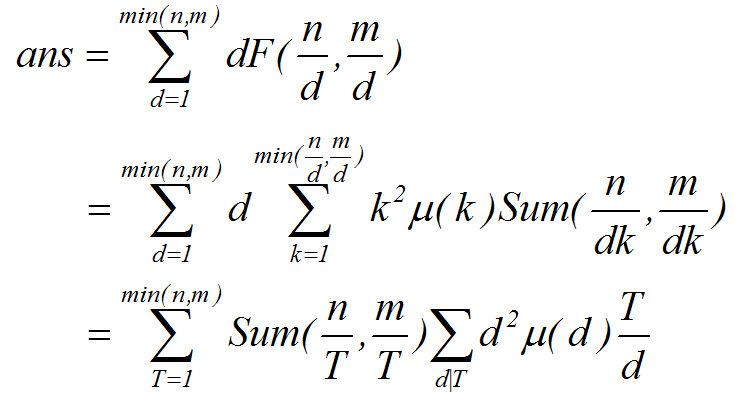
即后面那个部分为 H[T]，H[T]是积性函数，求详细证明的话将T和d展开为质因数次幂相乘的形式，考虑线性筛中枚举的质数与被筛数的性质即可

 #include<cmath>
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 typedef long long ll;
 const int maxn = 1e7 + ;
 const int mod = 1e8 + ;
 int cnt;
 int h[maxn];
 int pri[maxn];
 int sum[maxn];
 bool vis[maxn];
 inline void Scan(int &x)
 {
     char c;
     bool o = false;
     while(!isdigit(c = getchar())) o = (c != '-') ? o : true;
     x = c - '';
     while(isdigit(c = getchar())) x = x *  + c - '';
     if(o) x = -x;
 }
 inline void Sieve()
 {
     h[] = ;
     for(int i = ; i <= maxn; ++i)
     {
         if(!vis[i]) pri[++cnt] = i, h[i] = ((-(long long) i * i % mod) + mod + i) % mod;
         for(int j = ; j <= cnt; ++j)
         {
             int s = pri[j];
             long long k = (long long) i * s;
             if(k > maxn) break;
             vis[k] = true;
             if(!(i % s))
             {
                 h[k] = (long long) s * h[i] % mod;
                 break;
             }
             else h[k] = (long long) h[s] * h[i] % mod;
         }
     }
     for(int i = ; i <= maxn; ++i) sum[i] = (sum[i - ] + h[i]) % mod;
 }
 inline int Sum(int n, int m)
 {
     return ((long long) n * (n + ) >> ) % mod * (((long long) m * (m + ) >> ) % mod) % mod;
 }
 inline int Mobius(int n, int m)
 {
     int res = , last = ;
     if(n > m) swap(n, m);
     for(int i = ; i <= n; i = last + )
     {
         last = min(n / (n / i), m / (m / i));
         res = (res + (long long) Sum(n / i, m / i) * ((sum[last] - sum[i - ] + mod) % mod) % mod) % mod;
     }
     return res;
 }
 int main()
 {
     Sieve();
     int n;
     Scan(n);
     int a, b;
     while(n--)
     {
         Scan(a), Scan(b);
         printf("%d\n", Mobius(a, b));
     }
 }