焦作F Modular Production Line 费用流

题目链接

题解：这道题比赛的时候，学弟说是网络流，当时看N这么大，觉得网络流没法做，实际本题通过巧妙的建图，然后离散化。

先说下建图方式，首先每个覆盖区域，只有左右端点，如果我们只用左右端点的话，最多有400个点，所以第一步离散化。每个$i$和$i+1$连一条边流量为K，费用为0的边，每一个覆盖区域从左端点$u$向右端点$v$连一条流量为1，费用为$-w$的边，因为一般算最大费用，就要把边权变成负的算最小，最后取反是最大。对了，右端点$v$要+1，因为这个覆盖区域是从$u->v$，我应该从$v+1$开始流下一个。然后源点向最左端点连一条边流量为K，费用为0的边，汇点从最右端点连条相同的边。跑费用流即可。

为什么可行呢？

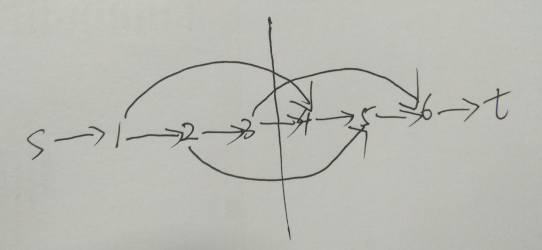
首先限制了总流量为K，那么流过离散化后的每个点最大流量是K，比如下面这个例子K=3，做一条纵向切线流量最多为3，保证了答案的正确性。

#include <bits/stdc++.h>
using namespace std;

const int maxn = ;
const int INF = 1e9;
int dist[maxn];
int pv[maxn],pe[maxn];
struct edge
{
    int to, cap, rev;
    int cost;
    edge(int a, int b, int c, int d)
    {
        to = a, cap = b, cost = c, rev = d;
    }
};
vector<edge> g[maxn];
void addedge(int from,int to,int cap,int cost)
{
    g[from].push_back(edge(to,cap,cost,g[to].size()));
    g[to].push_back(edge(from,,-cost,g[from].size()-));
}
int n;
int vis[maxn];
void SPFA(int s, int t)
{
    for(int i = ; i < maxn; i++) dist[i] = INF;
    memset(vis, , sizeof(vis));
    dist[s] = , vis[s] = ;
    queue<int> q;
    q.push(s);
    while(!q.empty())
    {
        int u = q.front();
        q.pop();
        vis[u] = ;
        for(int i = ; i < g[u].size(); i++)
        {
            edge &e = g[u][i];
            if(e.cap >  && (dist[e.to] - (dist[u] + e.cost)) > )
            {
                pv[e.to] = u, pe[e.to] = i;
                dist[e.to] = dist[u] + e.cost;
                if(!vis[e.to])
                {
                    vis[e.to] = ;
                    q.push(e.to);
                }
            }
        }
    }
}
int min_cost_flow(int s,int t,int f,int& max_flow)
{
    int ret = 0.0;
    while(f>)
    {
        SPFA(s, t);
        if(dist[t] == INF) return ret;///同一目的地，每次增广路都是最小费用
        ///当所有边的流量都流净后，即没有残余网络，返回。
        int d = f;
        for(int v=t;v!=s;v=pv[v])
        {
            d = min(d,g[pv[v]][pe[v]].cap);
        }
        f -= d;
        max_flow += d;
      //  printf("%d\n", ret);
        ret += (int)d*dist[t]; ///走一单位就消耗dist[t]
        for(int v=t;v!=s;v=pv[v])
        {
            edge &e = g[pv[v]][pe[v]];
            e.cap -= d;
            g[v][e.rev].cap += d;
        }
    }
    return ret;
}
int u[maxn], v[maxn], w[maxn], low[maxn];
int main()
{
    int T; scanf("%d", &T);
    while(T--)
    {
        int K, M, tmpn;
        scanf("%d %d %d", &tmpn, &K, &M);
        int cnt = ;
        for(int i = ; i <= M; i++)
        {
           scanf("%d %d %d", &u[i], &v[i], &w[i]);
           v[i]++; ///v[i]是我所占用的，要直接流到v[i]+1
           low[cnt++] = u[i];
           low[cnt++] = v[i];
        }
        sort(low, low + cnt);
        cnt = unique(low, low + cnt) - low;
        for(int i = ; i <= M; i++)
        {
            u[i] = lower_bound(low, low + cnt, u[i]) - low;
            v[i] = lower_bound(low, low + cnt, v[i]) - low;
        }
        for(int i = ; i <= M; i++)
        {
      //      printf("%d %d\n", u[i], v[i]);
        }
      //  printf("%d\n",cnt);
        for(int i = ; i < cnt + ; i++) g[i].clear();
        for(int i = ; i < cnt - ; i++)
        {
            addedge(i, i + , K, );
        }
        for(int i = ; i <= M; i++)
        {
            addedge(u[i], v[i], , -w[i]);
        }
        addedge(cnt + , , K, );
        addedge(cnt - , cnt + , K, );
        int maxflow = ;
        int ans = min_cost_flow(cnt + , cnt + , INF, maxflow);
        printf("%d\n", -ans);
    }
    return ;
}

Code