cf 701 E - Connecting Universities

Descrition

给你一颗\(n\le 2*10^5\)个点的树, 有\(2*k(2k\le n)\)座大学座落在点上

(任二大学不在同一个点)

求一种两两匹配的方案, 使得距离和最大

即\[maximize~\{~\sum_{each~pair~(x,y)} dis(x,y)~\}~\]

Solution 1

(1) 化简一下我们相当于要最小化 两两lca的深度和

我们先把这2k所大学按dfn序从小到大排好, 把前k个称为A部分, 后k个称为B部分

(2) 所有匹配均为\(A-B\)匹配

​ 如果存在一个\(A-A'\)匹配, 那么一定也会存在一个$B-B' $匹配

​ 此时通过交换匹配, 显然一定可以变优

(3) 引理: dfn区间[\(x,y\)]的公共lca 为 \(lca(x,r)\) 或 \(lca(l,r)\), 其中\(x\le l \le r\le y\)

​ 首先[x,y]的公共lca为点x,点y的lca是显然的

​ \(x\to r\)相当于走到子树或者向上回溯然后往下走

​ 如果\(x-r\)路径没有跨过lca, 如图1, 那么r-y就必定会跨过lca

​ 如果\(x-r\)路径跨国了lca, 如图2, 那么引理成立

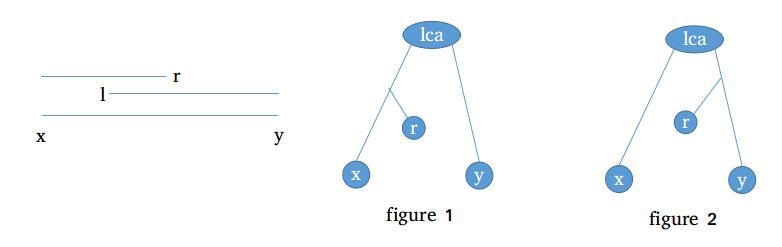
(4) 若\(x<y\in A\), 那么\(x' < y'\)

​ 如果存在\(x<y<y'<x'\) , 我们可以交换匹配变成\(x-y', y-x'\), 解不会变差

​ \(lca(x, x') < one~of~lca(x, y')~and~lca(y, x')\)

​ \(lca(y, y') < both~of~lca(x, y')~and~lca(y, x')\)

(5) 匹配为\(i\to i+k\)

​ 根据(2) , \(1\)至少要匹配到\(1+k\)的位置

​ 根据\((4)\), 必须要\(i\to i+k\), 才能保证匹配位置足够选择

Solution 2

考虑每条边\(fa\to x\)

记\(x\)子树内有\(sub[x]\)所大学

那么\(x\)子树外有\(2k-sub[x]\)所大学

结论: 每条边被匹配恰 \(min(sub[x], 2k- sub[x])\)次

​ 首先, 不可能超过这个次数

​ 然后, 如果小于, 那么子树内部有一对匹配, 子树外部有一对匹配

​ 通过交换匹配一定可以使得距离变长

知道每条边被匹配多少次后, 貌似可以用启发式合并vec的方式构造解

(行吧原题不要求构造解)