算法进阶面试题04——平衡二叉搜索树、AVL/红黑/SB树、删除和调整平衡的方法、输出大楼轮廓、累加和等于num的最长数组、滴滴Xor
接着第三课的内容和讲了第四课的部分内容
1、介绍二叉搜索树
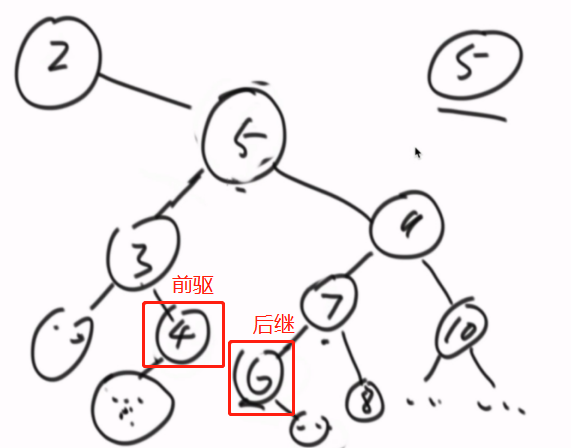
在二叉树上，何为一个节点的后继节点？
何为搜索二叉树？
如何实现搜索二叉树的查找？插入？删除？
二叉树的概念上衍生出的。
任何一个节点，左比他小，右比他大。标准搜索二叉树是没有重复值的。
TreeMap就是搜索二叉树，key是有序组织起来的，组织方式是搜索二叉树，具体就是红黑树（具有某一种平衡性的搜索二叉树），和HashMap的无序分布不同。
有序的话，能完成更多的事情，找刚刚小的、刚刚大的。
查数很方便，如果左子树和右子树高度差不超过一，每次搜索都筛选掉一半了。如果不平衡，会退变为O(n)的算法。
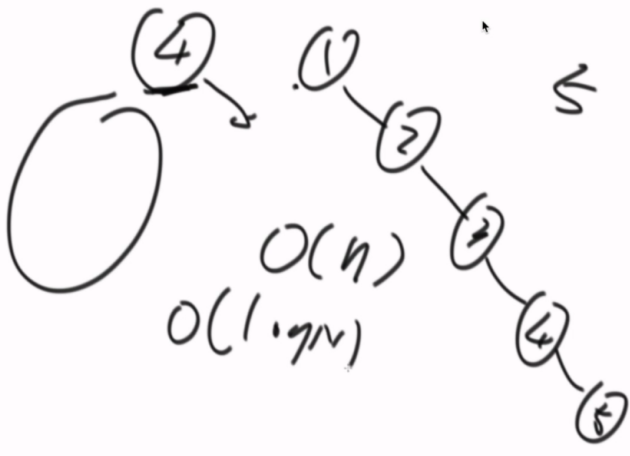
从搜索二叉树开始讲
树和插入树的顺序相关。
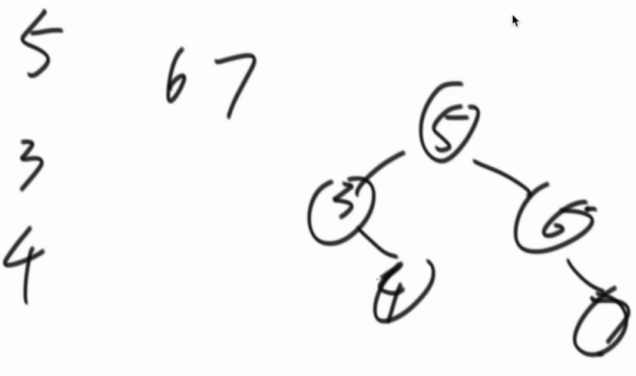
所以衍生了几种类型。
1、AVL，平衡性高度严苛，任何节点高度差都不超过一。O(logn)，很可能调整频率高。
2、红黑树，阉割了平衡性，每个节点染上色，头节点黑，叶节点黑，相邻不能出现红色节点。（这几年工程上越来越少用）
任何一条链，要求黑色的数量不能超过一。
如果尽最大能力插入红，最长和最短链的长度差也不会超过两倍。
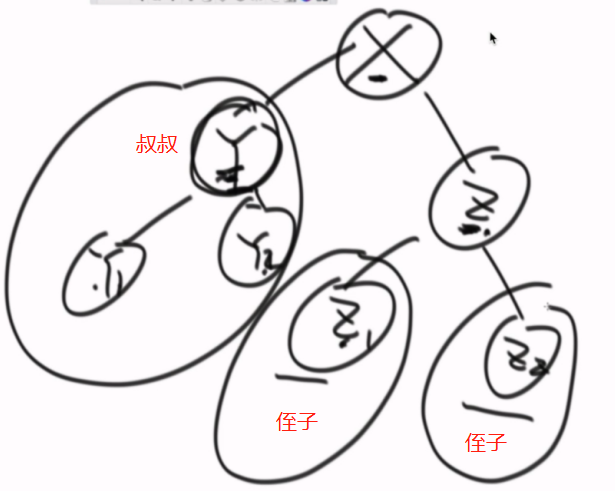
3、SB树（Size Balanced Tree），平衡性来自，任何一个叔叔节点的节点个数，不能少于任何一个侄子节点的节点个数。Y不能少于Z1或者Z2整颗树的节点数。
没必要都掌握，要理解为什么需要这些树，就是在修改最严苛的平衡性，做到每个节点来说，左右子树节点个数差不多的。
只是平衡性标准不一样。
目的为了调整不用那么频繁。
增删改查都是O(logn)。
package advanced_class_03; /**
* Not implemented by zuochengyun
*
* Abstract binary search tree implementation. Its basically fully implemented
* binary search tree, just template method is provided for creating Node (other
* trees can have slightly different nodes with more info). This way some code
* from standart binary search tree can be reused for other kinds of binary
* trees.
*
* @author Ignas Lelys
* @created Jun 29, 2011
*
*/
public class AbstractBinarySearchTree {//搜索二叉树 /** Root node where whole tree starts. */
public Node root; /** Tree size. */
protected int size; /**
* Because this is abstract class and various trees have different
* additional information on different nodes subclasses uses this abstract
* method to create nodes (maybe of class {@link Node} or maybe some
* different node sub class).
*
* @param value
* Value that node will have.
* @param parent
* Node's parent.
* @param left
* Node's left child.
* @param right
* Node's right child.
* @return Created node instance.
*/
protected Node createNode(int value, Node parent, Node left, Node right) {
return new Node(value, parent, left, right);
} /**
* Finds a node with concrete value. If it is not found then null is
* returned.
*
* @param element
* Element value.
* @return Node with value provided, or null if not found.
*/
public Node search(int element) {
Node node = root;
while (node != null && node.value != null && node.value != element) {
if (element < node.value) {
node = node.left;
} else {
node = node.right;
}
}
return node;
} /**
* Insert new element to tree.
*
* @param element
* Element to insert.
*/
public Node insert(int element) {
if (root == null) {
root = createNode(element, null, null, null);
size++;
return root;
}
//查找插入的父节点，找到不能再找
Node insertParentNode = null;
Node searchTempNode = root;
while (searchTempNode != null && searchTempNode.value != null) {
insertParentNode = searchTempNode;
if (element < searchTempNode.value) {
searchTempNode = searchTempNode.left;
} else {
searchTempNode = searchTempNode.right;
}
} Node newNode = createNode(element, insertParentNode, null, null);
if (insertParentNode.value > newNode.value) {
insertParentNode.left = newNode;
} else {
insertParentNode.right = newNode;
} size++;
return newNode;
} /**
* Removes element if node with such value exists.
*
* @param element
* Element value to remove.
*
* @return New node that is in place of deleted node. Or null if element for
* delete was not found.
*/
public Node delete(int element) {
Node deleteNode = search(element);
if (deleteNode != null) {
return delete(deleteNode);
} else {
return null;
}
} /**
* Delete logic when node is already found.
*
* @param deleteNode
* Node that needs to be deleted.
*
* @return New node that is in place of deleted node. Or null if element for
* delete was not found.
*/
protected Node delete(Node deleteNode) {
if (deleteNode != null) {
Node nodeToReturn = null;
if (deleteNode != null) {
if (deleteNode.left == null) {
nodeToReturn = transplant(deleteNode, deleteNode.right);
} else if (deleteNode.right == null) {
nodeToReturn = transplant(deleteNode, deleteNode.left);
} else {
Node successorNode = getMinimum(deleteNode.right);
if (successorNode.parent != deleteNode) {
transplant(successorNode, successorNode.right);
successorNode.right = deleteNode.right;
successorNode.right.parent = successorNode;
}
transplant(deleteNode, successorNode);
successorNode.left = deleteNode.left;
successorNode.left.parent = successorNode;
nodeToReturn = successorNode;
}
size--;
}
return nodeToReturn;
}
return null;
} /**
* Put one node from tree (newNode) to the place of another (nodeToReplace).
*
* @param nodeToReplace
* Node which is replaced by newNode and removed from tree.
* @param newNode
* New node.
*
* @return New replaced node.
*/
//相应的环境移交给newNode
private Node transplant(Node nodeToReplace, Node newNode) {
if (nodeToReplace.parent == null) {
this.root = newNode;
} else if (nodeToReplace == nodeToReplace.parent.left) {
nodeToReplace.parent.left = newNode;
} else {
nodeToReplace.parent.right = newNode;
}
if (newNode != null) {
newNode.parent = nodeToReplace.parent;
}
return newNode;
} /**
* @param element
* @return true if tree contains element.
*/
public boolean contains(int element) {
return search(element) != null;
} /**
* @return Minimum element in tree.
*/
public int getMinimum() {
return getMinimum(root).value;
} /**
* @return Maximum element in tree.
*/
public int getMaximum() {
return getMaximum(root).value;
} /**
* Get next element element who is bigger than provided element.
*
* @param element
* Element for whom descendand element is searched
* @return Successor value.
*/
// TODO Predecessor
public int getSuccessor(int element) {
return getSuccessor(search(element)).value;
} /**
* @return Number of elements in the tree.
*/
public int getSize() {
return size;
} /**
* Tree traversal with printing element values. In order method.
*/
public void printTreeInOrder() {
printTreeInOrder(root);
} /**
* Tree traversal with printing element values. Pre order method.
*/
public void printTreePreOrder() {
printTreePreOrder(root);
} /**
* Tree traversal with printing element values. Post order method.
*/
public void printTreePostOrder() {
printTreePostOrder(root);
} /*-------------------PRIVATE HELPER METHODS-------------------*/ private void printTreeInOrder(Node entry) {
if (entry != null) {
printTreeInOrder(entry.left);
if (entry.value != null) {
System.out.println(entry.value);
}
printTreeInOrder(entry.right);
}
} private void printTreePreOrder(Node entry) {
if (entry != null) {
if (entry.value != null) {
System.out.println(entry.value);
}
printTreeInOrder(entry.left);
printTreeInOrder(entry.right);
}
} private void printTreePostOrder(Node entry) {
if (entry != null) {
printTreeInOrder(entry.left);
printTreeInOrder(entry.right);
if (entry.value != null) {
System.out.println(entry.value);
}
}
} protected Node getMinimum(Node node) {
while (node.left != null) {
node = node.left;
}
return node;
} protected Node getMaximum(Node node) {
while (node.right != null) {
node = node.right;
}
return node;
} protected Node getSuccessor(Node node) {
// if there is right branch, then successor is leftmost node of that
// subtree
if (node.right != null) {
return getMinimum(node.right);
} else { // otherwise it is a lowest ancestor whose left child is also
// ancestor of node
Node currentNode = node;
Node parentNode = node.parent;
while (parentNode != null && currentNode == parentNode.right) {
// go up until we find parent that currentNode is not in right
// subtree.
currentNode = parentNode;
parentNode = parentNode.parent;
}
return parentNode;
}
} // -------------------------------- TREE PRINTING
// ------------------------------------ public void printTree() {
printSubtree(root);
} public void printSubtree(Node node) {
if (node.right != null) {
printTree(node.right, true, "");
}
printNodeValue(node);
if (node.left != null) {
printTree(node.left, false, "");
}
} private void printNodeValue(Node node) {
if (node.value == null) {
System.out.print("<null>");
} else {
System.out.print(node.value.toString());
}
System.out.println();
} private void printTree(Node node, boolean isRight, String indent) {
if (node.right != null) {
printTree(node.right, true, indent + (isRight ? " " : " | "));
}
System.out.print(indent);
if (isRight) {
System.out.print(" /");
} else {
System.out.print(" \\");
}
System.out.print("----- ");
printNodeValue(node);
if (node.left != null) {
printTree(node.left, false, indent + (isRight ? " | " : " "));
}
} public static class Node {
public Node(Integer value, Node parent, Node left, Node right) {
super();
this.value = value;
this.parent = parent;
this.left = left;
this.right = right;
} public Integer value;
public Node parent;
public Node left;
public Node right; public boolean isLeaf() {
return left == null && right == null;
} @Override
public int hashCode() {
final int prime = 31;
int result = 1;
result = prime * result + ((value == null) ? 0 : value.hashCode());
return result;
} @Override
public boolean equals(Object obj) {
if (this == obj)
return true;
if (obj == null)
return false;
if (getClass() != obj.getClass())
return false;
Node other = (Node) obj;
if (value == null) {
if (other.value != null)
return false;
} else if (!value.equals(other.value))
return false;
return true;
} }
}
搜索二叉树实现代码
删除逻辑：
如果删除的节点没有左孩子，直接让右孩子顶替上去。
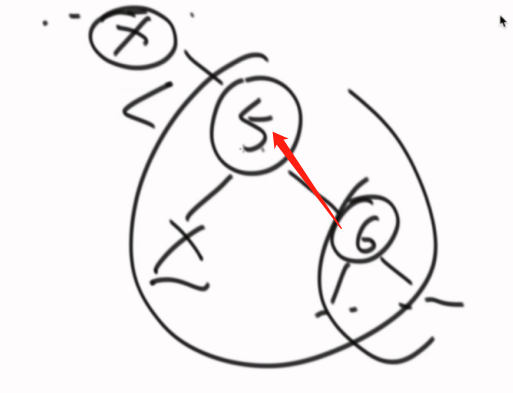
如果没有右孩子，左孩子变成x的右孩子，把5从环境分离，将4顶替上去。
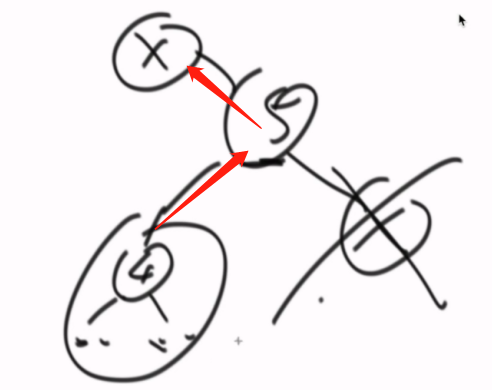
左右双全怎么办？
右子树最左的节点6去顶。（最小的比他大的数）（后继节点）
左接管3、右接管9
6的右子树移交给7（父的左边）。
拿前驱节点去顶替也可以。（中序遍历是有顺序的）
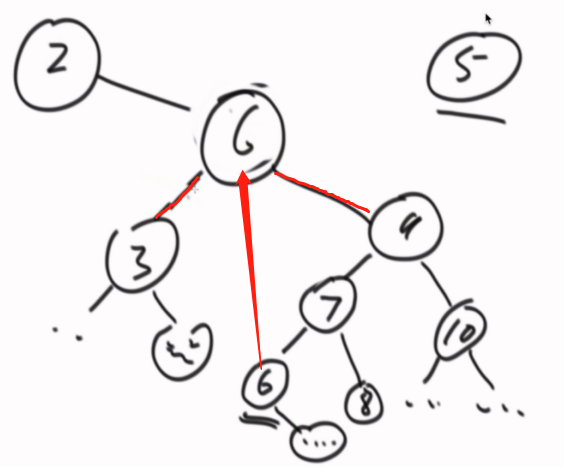
所有类型的搜索二叉树，调整的基本动作都是一样的。
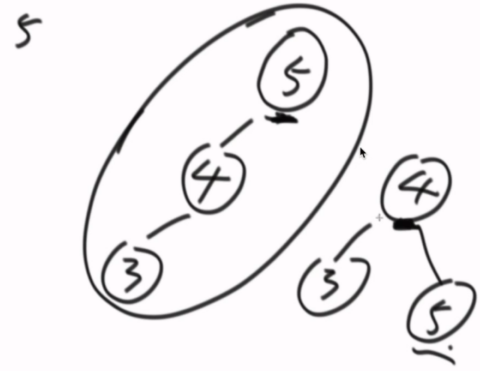
左旋右旋（顺/逆时针旋）
只是动作的组合不一样。4种组合。
右旋。顺时针旋
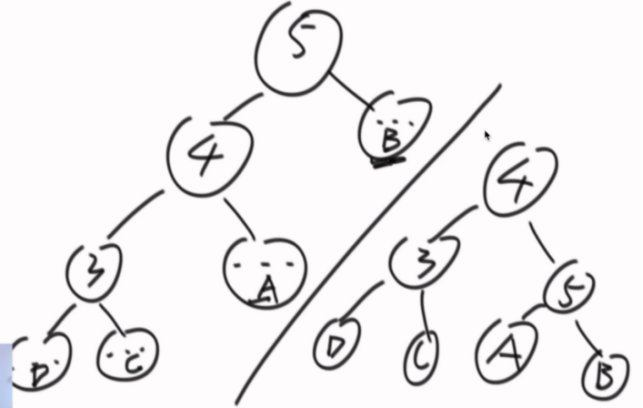
左旋，逆时针选
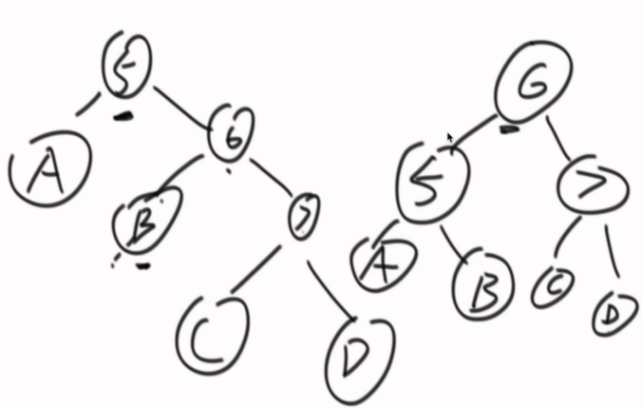
怎么使用这些动作？
AVL怎么发现不平衡，节点存储当前层数，通过查看左右子树，获得他们分别能到达的层数，每插入一个数，都会回溯到之前的节点，更改能达到的层数，如果发现不平衡自然会调整，逐个向上检查。
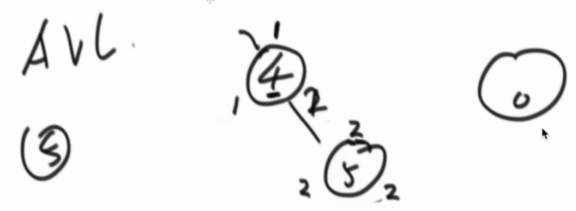
改的过程中，能知道不平衡
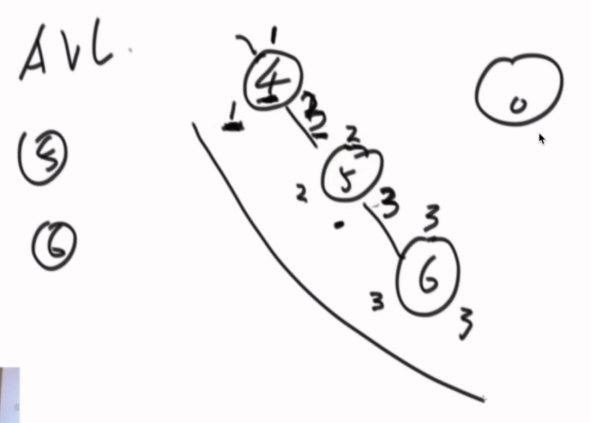
调整组合有四种，LL,RR,LR,RL
LL
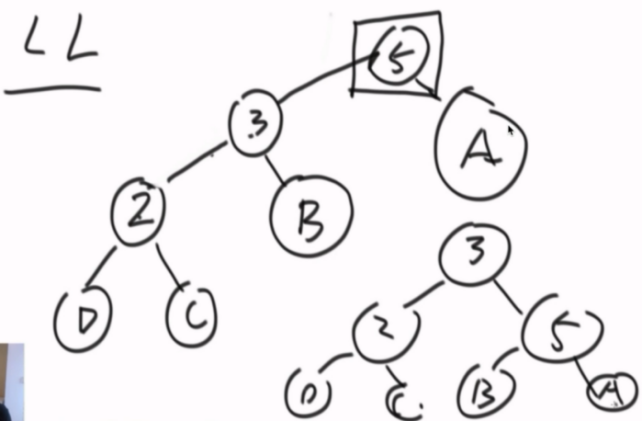
RR，左旋一下就行。
LL和RR形出现单一动作就够了。
LR的情况，先对5的左子树进行左旋转，然后在进行右旋
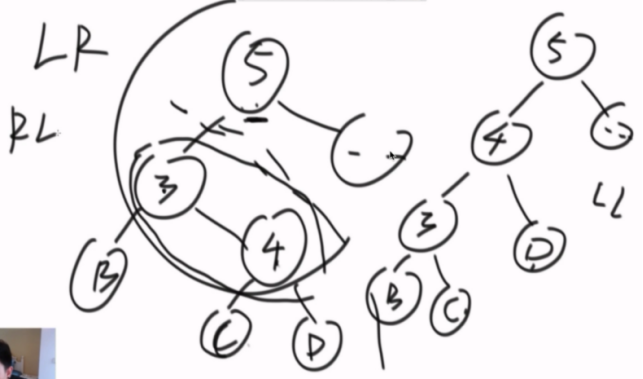
然后进行LL操作。
LR形也同理。
具体实现看代码。
package advanced_class_03; /**
* Not implemented by zuochengyun
*
* Abstract class for self balancing binary search trees. Contains some methods
* that is used for self balancing trees.
*
* @author Ignas Lelys
* @created Jul 24, 2011
*
*/
public abstract class AbstractSelfBalancingBinarySearchTree extends AbstractBinarySearchTree { /**
* Rotate to the left.
*
* @param node Node on which to rotate.
* @return Node that is in place of provided node after rotation.
*/
protected Node rotateLeft(Node node) {
Node temp = node.right;
temp.parent = node.parent; node.right = temp.left;
if (node.right != null) {
node.right.parent = node;
} temp.left = node;
node.parent = temp; // temp took over node's place so now its parent should point to temp
if (temp.parent != null) {
if (node == temp.parent.left) {
temp.parent.left = temp;
} else {
temp.parent.right = temp;
}
} else {
root = temp;
} return temp;
} /**
* Rotate to the right.
*
* @param node Node on which to rotate.
* @return Node that is in place of provided node after rotation.
*/
protected Node rotateRight(Node node) {
Node temp = node.left;
temp.parent = node.parent; node.left = temp.right;
if (node.left != null) {
node.left.parent = node;
} temp.right = node;
node.parent = temp; // temp took over node's place so now its parent should point to temp
if (temp.parent != null) {
if (node == temp.parent.left) {
temp.parent.left = temp;
} else {
temp.parent.right = temp;
}
} else {
root = temp;
} return temp;
} }
加入自调整方法的二叉搜索树
package advanced_class_03; /**
* Not implemented by zuochengyun
*
* AVL tree implementation.
*
* In computer science, an AVL tree is a self-balancing binary search tree, and
* it was the first such data structure to be invented.[1] In an AVL tree, the
* heights of the two child subtrees of any node differ by at most one. Lookup,
* insertion, and deletion all take O(log n) time in both the average and worst
* cases, where n is the number of nodes in the tree prior to the operation.
* Insertions and deletions may require the tree to be rebalanced by one or more
* tree rotations.
*
* @author Ignas Lelys
* @created Jun 28, 2011
*
*/
public class AVLTree extends AbstractSelfBalancingBinarySearchTree { /**
* @see trees.AbstractBinarySearchTree#insert(int)
*
* AVL tree insert method also balances tree if needed. Additional
* height parameter on node is used to track if one subtree is higher
* than other by more than one, if so AVL tree rotations is performed
* to regain balance of the tree.
*/
@Override
public Node insert(int element) {
Node newNode = super.insert(element);
rebalance((AVLNode)newNode);
return newNode;
} /**
* @see trees.AbstractBinarySearchTree#delete(int)
*/
@Override
public Node delete(int element) {
Node deleteNode = super.search(element);
if (deleteNode != null) {
Node successorNode = super.delete(deleteNode);
if (successorNode != null) {
// if replaced from getMinimum(deleteNode.right) then come back there and update heights
AVLNode minimum = successorNode.right != null ? (AVLNode)getMinimum(successorNode.right) : (AVLNode)successorNode;
recomputeHeight(minimum);
rebalance((AVLNode)minimum);
} else {
recomputeHeight((AVLNode)deleteNode.parent);
rebalance((AVLNode)deleteNode.parent);
}
return successorNode;
}
return null;
} /**
* @see trees.AbstractBinarySearchTree#createNode(int, trees.AbstractBinarySearchTree.Node, trees.AbstractBinarySearchTree.Node, trees.AbstractBinarySearchTree.Node)
*/
@Override
protected Node createNode(int value, Node parent, Node left, Node right) {
return new AVLNode(value, parent, left, right);
} /**
* Go up from inserted node, and update height and balance informations if needed.
* If some node balance reaches 2 or -2 that means that subtree must be rebalanced.
*
* @param node Inserted Node.
*/
private void rebalance(AVLNode node) {
while (node != null) { Node parent = node.parent; int leftHeight = (node.left == null) ? -1 : ((AVLNode) node.left).height;
int rightHeight = (node.right == null) ? -1 : ((AVLNode) node.right).height;
int nodeBalance = rightHeight - leftHeight;
// rebalance (-2 means left subtree outgrow, 2 means right subtree)
if (nodeBalance == 2) {
if (node.right.right != null) {
node = (AVLNode)avlRotateLeft(node);
break;
} else {
node = (AVLNode)doubleRotateRightLeft(node);
break;
}
} else if (nodeBalance == -2) {//左树超了
if (node.left.left != null) {
node = (AVLNode)avlRotateRight(node);
break;
} else {
node = (AVLNode)doubleRotateLeftRight(node);
break;
}
} else {
updateHeight(node);
} node = (AVLNode)parent;
}
} /**
* Rotates to left side.
*/
private Node avlRotateLeft(Node node) {
Node temp = super.rotateLeft(node); updateHeight((AVLNode)temp.left);
updateHeight((AVLNode)temp);
return temp;
} /**
* Rotates to right side.
*/
private Node avlRotateRight(Node node) {
Node temp = super.rotateRight(node); updateHeight((AVLNode)temp.right);
updateHeight((AVLNode)temp);
return temp;
} /**
* Take right child and rotate it to the right side first and then rotate
* node to the left side.
*/
protected Node doubleRotateRightLeft(Node node) {
node.right = avlRotateRight(node.right);
return avlRotateLeft(node);
} /**
* Take right child and rotate it to the right side first and then rotate
* node to the left side.
*/
protected Node doubleRotateLeftRight(Node node) {
node.left = avlRotateLeft(node.left);
return avlRotateRight(node);
} /**
* Recomputes height information from the node and up for all of parents. It needs to be done after delete.
*/
private void recomputeHeight(AVLNode node) {
while (node != null) {
node.height = maxHeight((AVLNode)node.left, (AVLNode)node.right) + 1;
node = (AVLNode)node.parent;
}
} /**
* Returns higher height of 2 nodes.
*/
private int maxHeight(AVLNode node1, AVLNode node2) {
if (node1 != null && node2 != null) {
return node1.height > node2.height ? node1.height : node2.height;
} else if (node1 == null) {
return node2 != null ? node2.height : -1;
} else if (node2 == null) {
return node1 != null ? node1.height : -1;
}
return -1;
} /**
* Updates height and balance of the node.
*
* @param node Node for which height and balance must be updated.
*/
private static final void updateHeight(AVLNode node) {
int leftHeight = (node.left == null) ? -1 : ((AVLNode) node.left).height;
int rightHeight = (node.right == null) ? -1 : ((AVLNode) node.right).height;
node.height = 1 + Math.max(leftHeight, rightHeight);
} /**
* Node of AVL tree has height and balance additional properties. If balance
* equals 2 (or -2) that node needs to be re balanced. (Height is height of
* the subtree starting with this node, and balance is difference between
* left and right nodes heights).
*
* @author Ignas Lelys
* @created Jun 30, 2011
*
*/
protected static class AVLNode extends Node {
public int height; public AVLNode(int value, Node parent, Node left, Node right) {
super(value, parent, left, right);
}
} }
AVL树实现代码
如果是红黑树，插入组合5种，删除8种。
只需会用即可，只要理解平衡性来自左右子树规模差不多（为了每次效率都是logn），了解左右旋动作。
怎么用？
可以查最大值，都是o(logn)，hashMap只能逐个找。
找到刚好比某数大/小的值。
package advanced_class_03;
import java.util.TreeMap;
public class TestTreeMap {
public static void main(String[] args) {
TreeMap<Integer,String> treeMap = new TreeMap<>();
treeMap.put(5,"xie");
treeMap.put(10,"yu");
treeMap.put(25,"peng");
treeMap.put(15,"ni");
treeMap.put(20,"hao");
System.out.println(treeMap.get(10));
System.out.println(treeMap.lastKey());
System.out.println(treeMap.firstKey());
System.out.println(treeMap.ceilingKey(12));
System.out.println(treeMap.floorKey(12));
}
}
需要数组按序组织，就用TreeMap，平衡搜索二叉树。
开始第四课
LeetCode三大顶级难题之一（频度两年出一次）
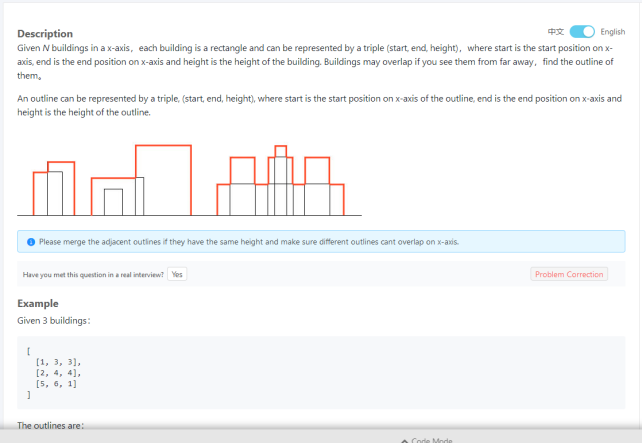
给定一个N行3列二维数组，每一行表示有一座大楼，一共有N座大楼。 所有大楼的底部都坐落在X轴上，每一行的三个值(a,b,c)代表每座大楼的从(a,0)点开始，到 (b,0)点结束，高度为c。 输入的数据可以保证a<b,且a，b，c均为正数。大楼之间可以有重合。 请输出整体的轮廓线。
例子：给定一个二维数组 [ [1, 3, 3], [2, 4, 4], [5, 6,1] ]
输出为轮廓线 [ [1, 2, 3], [2, 4, 4], [5, 6, 1] ]
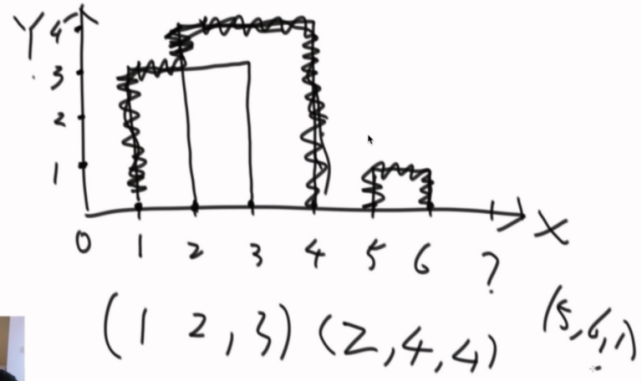
处理方式：
每个大楼拆成两个信息，(1,3,上)、(3,3,下)，1这个地方有高度3上去了，3这个地方有高度3下去了。
然后按位置进行排序，(1,3,上)(2,4,上)(3,3,下)....
一个轮廓产生一定是最大高度发生变化了。
位置排好序后，建立一张TreeMap，
遍历排序的同时，利用TreeMap（<高度,次数>）为辅助，加入当前值的高度信息后，改变TreeMap高度信息，查看当前的最大高度是否有改变。
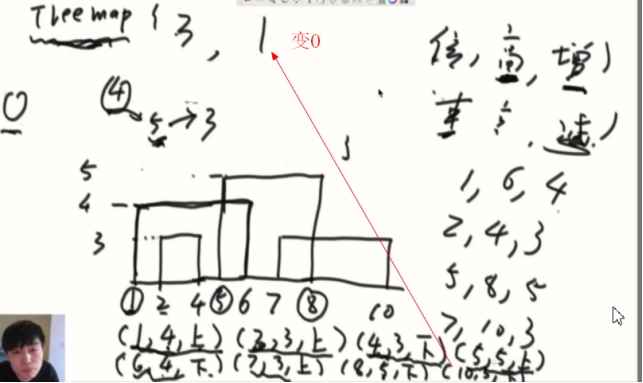
得出1,5,8,10会产生轮廓。
最大高度的变化来描述轮廓的产生行为，怎么在很多高度存在的时候，最快的找到最大高度，于是就想到用TreeMap结构，用搜索二叉树找是最快的。
package advanced_class_04; import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.List;
import java.util.Map.Entry;
import java.util.TreeMap; public class Code_01_Building_Outline { public static class Node {//高度 位置 上/下
public boolean isUp;
public int posi;
public int h; public Node(boolean bORe, int position, int height) {
isUp = bORe;
posi = position;
h = height;
}
} public static class NodeComparator implements Comparator<Node> {
@Override
public int compare(Node o1, Node o2) {
if (o1.posi != o2.posi) {
return o1.posi - o2.posi;
}
// if (o1.isUp != o2.isUp) {
// return o1.isUp ? -1 : 1;
// }
return 0;
}
} public static List<List<Integer>> buildingOutline(int[][] buildings) {
Node[] nodes = new Node[buildings.length * 2];
for (int i = 0; i < buildings.length; i++) {
nodes[i * 2] = new Node(true, buildings[i][0], buildings[i][2]);
nodes[i * 2 + 1] = new Node(false, buildings[i][1], buildings[i][2]);
}
Arrays.sort(nodes, new NodeComparator());//按照位置排序
//存高度，次数
TreeMap<Integer, Integer> htMap = new TreeMap<>();//高度信息
TreeMap<Integer, Integer> pmMap = new TreeMap<>();//位置信息
for (int i = 0; i < nodes.length; i++) {
if (nodes[i].isUp) {//向上，加一
if (!htMap.containsKey(nodes[i].h)) {
htMap.put(nodes[i].h, 1);
} else {
htMap.put(nodes[i].h, htMap.get(nodes[i].h) + 1);
}
} else {//向下，减一
if (htMap.containsKey(nodes[i].h)) {
if (htMap.get(nodes[i].h) == 1) {
htMap.remove(nodes[i].h);
} else {
htMap.put(nodes[i].h, htMap.get(nodes[i].h) - 1);
}
}
}
//收集每个位置的最大高度
if (htMap.isEmpty()) {
pmMap.put(nodes[i].posi, 0);
} else {
pmMap.put(nodes[i].posi, htMap.lastKey());
}
}
List<List<Integer>> res = new ArrayList<>();
int start = 0;
int height = 0;
for (Entry<Integer, Integer> entry : pmMap.entrySet()) {
int curPosition = entry.getKey();
int curMaxHeight = entry.getValue();
//当前高度和之前的不同，开始产生轮廓线
if (height != curMaxHeight) {
//不等于0证明之前已经记录了开始，要收尾了
if (height != 0) {
List<Integer> newRecord = new ArrayList<Integer>();
newRecord.add(start);
newRecord.add(curPosition);
newRecord.add(height);
res.add(newRecord);
}
//等于0的话，才刚开始生成轮廓线
start = curPosition;
height = curMaxHeight;
}
}
return res;
} public static void main(String[] args) {
int[][] test = new int[][]{
{1, 3, 3}, {2, 4, 4}, {5, 6, 1}
}; List<List<Integer>> buildingOutLine = buildingOutline(test); for (List<Integer> list : buildingOutLine) {
for (Integer i : list) {
System.out.printf(i + " ");
}
System.out.println();
}
} }
如果相同的位置下，上的高度排在前面（也可以不这么排），先加入低高度的，再减去高高度的，轮廓会被低高度的顶一下。
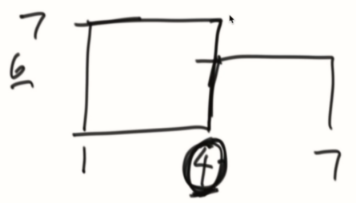
pmMap，记录每个位置的最大高度，因为3位置有个4落下来，所以会是2。
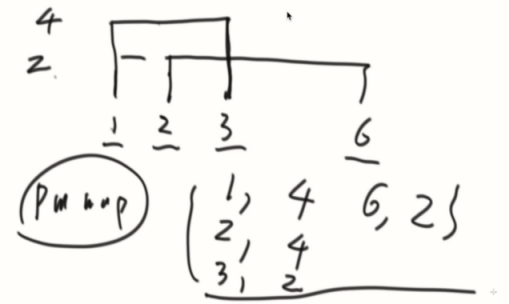
利用pmMap重建轮廓信息
高度不变的不用管，高度改变了证明之前的轮廓线结束，新的轮廓线开始。
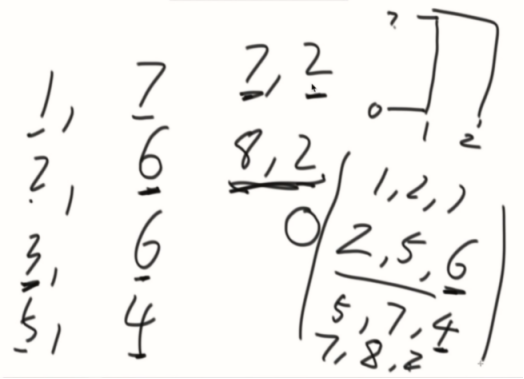
中间有0的情况
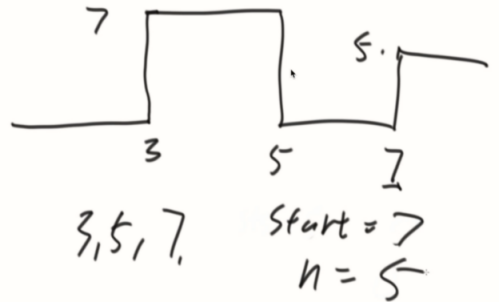
题目二：
给定一个数组arr（有0、正、负），和一个整数num，求在arr中，累加和等于num的最长子数组的长度
例子：
arr = {7,3,2,1,1,7,7,7} num = 7
其中有很多的子数组累加和等于7，但是最长的子数组是{3,2,1,1}，所以返回其长度4
普遍思路：必须以每个位置结尾的情况下，如果求出答案，那答案一定在其中。
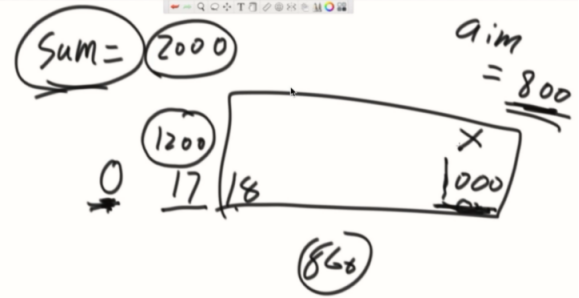
以100位结尾，从0~1000sum为2000，如果发现0~17位1200，那么18~1000就是我们要求的以1000结尾最长数组。
操作如下：
准备一个sum每走一步就累加，准备一个map记录第一次出现累加数据的位置，默认加入0,-1因为累加0不需要任何数据参与。
然后每走一步都把sum-aim，然后去map中找，第一次出现sum-aim的值的位置
如果有就是这个位置+1~当前位置可以出现aim，记录长度
如果没有就加入到map中（注意只加第一次出现的位置，后面再遇见用样的数都不更新）然后继续下一步...
默认加入0,-1，是因为不错过从0开始出现答案的机会，因为我们的结论是查出一个位置是从这个位置开始的下一个位置开始算的。
package advanced_class_04;
import java.util.HashMap;
public class Code_05_LongestSumSubArrayLength {
public static int maxLength(int[] arr, int aim) {
if (arr == null || arr.length == 0) {
return 0;
}
HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();
map.put(0, -1); // important
int len = 0;
int sum = 0;
for (int i = 0; i < arr.length; i++) {
sum += arr[i];
if (map.containsKey(sum - aim)) {
len = Math.max(i - map.get(sum - aim), len);
}
if (!map.containsKey(sum)) {
map.put(sum, i);
}
}
return len;
}
public static int[] generateArray(int size) {
int[] result = new int[size];
for (int i = 0; i != size; i++) {
result[i] = (int) (Math.random() * 11) - 5;
}
return result;
}
public static void printArray(int[] arr) {
for (int i = 0; i != arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int[] arr = generateArray(20);
printArray(arr);
System.out.println(maxLength(arr, 10));
}
}
扩展：
一个数组中，只有整数，有奇数偶数，求奇数和偶数个数相等的最长子数组。
做法：把奇数改为1，偶数改为-1，把累加和为0的最长子数组查出即可。
数组中只有1和0的话，也同理把0改为-1，计算出累加和为0的最长子数组即可。
数组中只有0、1、2的话，求1、2数量相等的最长子数组，把2变-1，技巧同理。
思考这题，算法原型是最长累加和问题：（拆分比较麻烦）
定义数组的异或和的概念：
数组中所有的数异或起来，得到的结果叫做数组的异或和，
比如数组{3,2,1}的异或和是，3^2^1 = 0
给定一个数组arr，你可以任意把arr分成很多不相容的子数组，你的目的是：
分出来的子数组中，异或和为0的子数组最多。
请返回：分出来的子数组中，异或和为0的子数组最多是多少？
首先要理解下异或运算，
1、异或运算满足交换律和结合律，一组数异或结果和异或顺序无关。
2、0和任何数异或都是那个数。0^n=n、n^n=0
我们求0~i范围最多能切出几个异或和为0的子数组。
然后求0~i+1的范围。
依次求到0~n-1。
0~i，一定存在一个最优划分，那么i作为最后一个部分的最后一个数，有两种可能性。
1、i所在的部分，不是为0的子数组
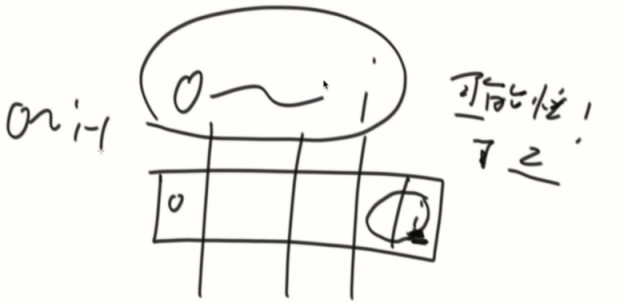
0~i最多能划多少块和0~i-1最多能划多少块，数量一定相等。（说白了就是要你和不要你有什么区别呢）
一个dp问题，决定的时候用到了之前的算法原型。
2、i所在的部分，是为0的子数组
k一定是左边离i最近的异或和为0的位置。中间不可能存在一个j~i是异或和0。
0~i异或结果是sum，那就是在找0~i-1中间，异或还是sum的最晚的位置。那个最晚的位置的下一个位置就是k的位置。
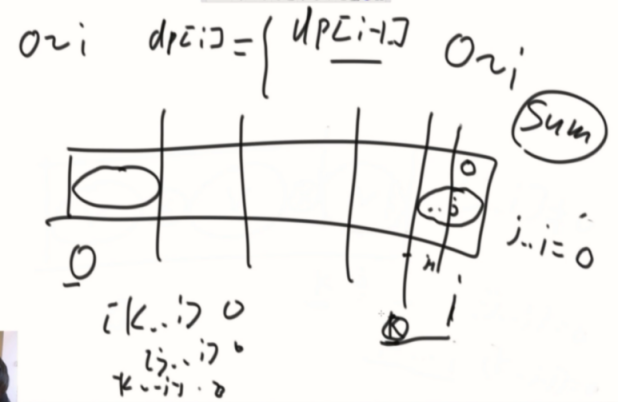
k~i这个部分在哪呢？
就是之前有没有出现过相同的异或和，他最晚的位置在哪里，那个位置就是k位置。
dp在两种决策中选最大的，就是答案。
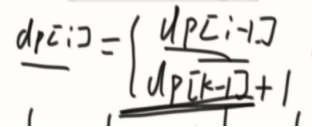
这个变成了，找一个异或和最晚出现的位置。
出处2018年滴滴校招的原题。
理清思路：
思路
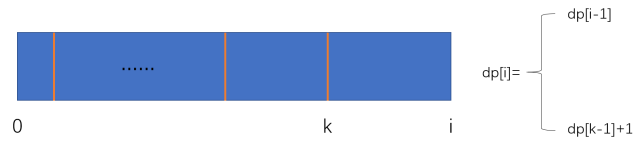
DP，假设数组最后一个数的下标是 i，并且数组存在一个最优划分，使得划分的子数组个数最多，那么 i 有两种情况，第一，i 所在的划分区间异或为 0；第二，i 所在的划分区间，异或不为 0。对于第一种情况 dp[i] = dp[i-1] 的，对于第二种情况，假设 i 的最优划分区间是 [k,i]，0 到 i 的连续异或为 sum，只要求出一个最大的下标 k-1，使得 0 到 k-1 的异或也为 sum 就行了
package advanced_class_04;
import java.util.HashMap;
public class Code_06_Most_EOR {
public static int mostEOR(int[] arr) {
int ans = 0;
int xor = 0;//异或，英文为exclusive OR，缩写成xor
int[] dp = new int[arr.length];
HashMap<Integer, Integer> map = new HashMap<>();
map.put(0, -1);//一个数都没有的时候，异或和为0
for (int i = 0; i < arr.length; i++) {
xor ^= arr[i];
if (map.containsKey(xor)) {//存在证明异或和区域+1
int pre = map.get(xor);
dp[i] = pre == -1 ? 1 : (dp[pre] + 1);
}
if (i > 0) {//拿最优情况,类似贪心
dp[i] = Math.max(dp[i - 1], dp[i]);
}
//求最晚的位置，所以每次都更新
map.put(xor, i);
ans = Math.max(ans, dp[i]);
}
return ans;
}
// for test
public static int comparator(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
int[] eors = new int[arr.length];
int eor = 0;
for (int i = 0; i < arr.length; i++) {
eor ^= arr[i];
eors[i] = eor;
}
int[] mosts = new int[arr.length];
mosts[0] = arr[0] == 0 ? 1 : 0;
for (int i = 1; i < arr.length; i++) {
mosts[i] = eors[i] == 0 ? 1 : 0;
for (int j = 0; j < i; j++) {
if ((eors[i] ^ eors[j]) == 0) {
mosts[i] = Math.max(mosts[i], mosts[j] + 1);
}
}
mosts[i] = Math.max(mosts[i], mosts[i - 1]);
}
return mosts[mosts.length - 1];
}
// for test
public static int[] generateRandomArray(int maxSize, int maxValue) {
int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) ((maxValue + 1) * Math.random());
}
return arr;
}
// for test
public static void printArray(int[] arr) {
if (arr == null) {
return;
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
// for test
public static void main(String[] args) {
int testTime = 500000;
int maxSize = 300;
int maxValue = 100;
boolean succeed = true;
for (int i = 0; i < testTime; i++) {
int[] arr = generateRandomArray(maxSize, maxValue);
int res = mostEOR(arr);
int comp = comparator(arr);
if (res != comp) {
succeed = false;
printArray(arr);
System.out.println(res);
System.out.println(comp);
break;
}
}
System.out.println(succeed ? "Nice!" : "Fucking fucked!");
}
}
算法进阶面试题04——平衡二叉搜索树、AVL/红黑/SB树、删除和调整平衡的方法、输出大楼轮廓、累加和等于num的最长数组、滴滴Xor的更多相关文章
- 看动画学算法之:平衡二叉搜索树AVL Tree
目录 简介 AVL的特性 AVL的构建 AVL的搜索 AVL的插入 AVL的删除 简介 平衡二叉搜索树是一种特殊的二叉搜索树.为什么会有平衡二叉搜索树呢? 考虑一下二叉搜索树的特殊情况,如果一个二叉搜 ...
- 二叉搜索树、AVL平衡二叉搜索树、红黑树、多路查找树
1.二叉搜索树 1.1定义 是一棵二叉树,每个节点一定大于等于其左子树中每一个节点,小于等于其右子树每一个节点 1.2插入节点 从根节点开始向下找到合适的位置插入成为叶子结点即可:在向下遍历时,如果要 ...
- 平衡二叉搜索树AVL
package com.sunshine.AlgorithmTemplate; import com.sunshine.OFFER66_SECOND.BalanceTreeNode; import c ...
- 平衡二叉搜索树/AVL二叉树 C实现
//AVTree.h #ifndef MY_AVLTREE_H #define MY_AVLTREE_H typedef int ElementType; struct TreeNode { Elem ...
- 算法：非平衡二叉搜索树（UnBalanced Binary Search Tree）
背景 很多场景下都需要将元素存储到已排序的集合中.用数组来存储,搜索效率非常高: O(log n),但是插入效率比较低:O(n).用链表来存储,插入效率和搜索效率都比较低:O(n).如何能提供插入和搜 ...
- C++版 - 剑指offer 面试题63：二叉搜索树的第k个结点(二叉树中序遍历的应用) 题解
面试题 63:二叉搜索树的第k个结点 题目:给定一颗二叉搜索树,请找出其中的第k大的结点.例如, 5 / \ 3 7 /\ /\ 2 4 6 8 (见下面的图1) 中,按结点数值大小顺序第三个结点的值 ...
- C++版 - 剑指offer 面试题24：二叉搜索树BST的后序遍历序列(的判断) 题解
剑指offer 面试题24:二叉搜索树的后序遍历序列(的判断) 题目:输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果.如果是则返回true.否则返回false.假设输入的数组的任意两个 ...
- convert sorted list to binary search tree(将有序链表转成平衡二叉搜索树)
Given a singly linked list where elements are sorted in ascending order, convert it to a height bala ...
- LeetCode 将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树
第108题 将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树. 本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1. 示例: 给定有序数组: [-10 ...
随机推荐
- weblogic对JSP预编译、weblogic读取JSP编译后的class文件、ant中weblogic.jspc预编译JSP
我们都知道在weblogic中JSP是每次第一次访问的时候才会编译,这就造成第一次访问某个JSP的时候性能下降,有时候我们也希望JSP被编译成class然后打包在jar中实现隐藏JSP的功能,下面介绍 ...
- Python|绝不乱入的靠谱书单
- UML和模式应用4：初始阶段(1)--概述
1.前言 UP开发包括四个阶段:初始阶段.细化阶段.构建阶段.移交阶段: 初始阶段是项目比较简短的起始步骤,主要目的是收集足够的信息来建立共同设想,调查项目的总体目标和可行性,确定是否值得进一步深入. ...
- kafka系列八、kafka消息重复和丢失的场景及解决方案分析
消息重复和丢失是kafka中很常见的问题,主要发生在以下三个阶段: 生产者阶段 broke阶段 消费者阶段 一.生产者阶段重复场景 1.根本原因 生产发送的消息没有收到正确的broke响应,导致pro ...
- (并发编程)线程 (理论-创建-lock-属性-守护，与进程的对比)
一.线程理论1.什么是线程 线程指的是一条流水线的工作过程(执行代码) 进程不是执行单位,是资源单位 一个进程内自带一个线程,线程是执行单位 2.进程VS线程 1.同一进程内的线程们 ...
- 重新学习angularjs--第一篇（入门）
几乎是一年之前,泛泛接触了angularjs,也做了一些项目,但是时至今日,几乎已经忘记了ng的使用,由于业务需要,近日要攻克这座难关,重新学习.会把学习的一些东西拿出来,记录之. angularjs ...
- PHP获取网卡的MAC地址原码;目前支持WIN/LINUX系统 获取机器网卡的物理(MAC)地址
声明转换于其它博客当中的. <?php /** 获取网卡的MAC地址原码:目前支持WIN/LINUX系统 获取机器网卡的物理(MAC)地址 **/ class GetMacAddr{ var $ ...
- PYTHON-绑定方法 反射 内置函数
'''绑定方法类中定义函数分为了两大类: 1. 绑定方法 特殊之处: 绑定给谁就应该由谁来调用,谁来调用就会将谁当做第一个参数自动传入 如何用: 绑定给对象的方法: 在类中定义函数没有被任何装饰器修饰 ...
- vue系列之项目结构
参考地址:链接 build webpack配置相关 config webpack配置相关 node_modules npm install 安装的依赖代码库 src 存放项目源码 static 存 ...
- python之抽象基类
抽象基类特点 1.不能够实例化 2.在这个基础的类中设定一些抽象的方法,所有继承这个抽象基类的类必须覆盖这个抽象基类里面的方法 思考 既然python中有鸭子类型,为什么还要使用抽象基类? 一是我们在 ...