一、项目WEB视图结构

　　注释：struts.xml：最普通配置，任何无特殊配置

二、访问页面

　　1.访问root.jsp

//方式1：

http://localhost/demo/root.jsp

//方式2：

http://localhost/demo/

　　2.访问index.jsp[暂无办法]

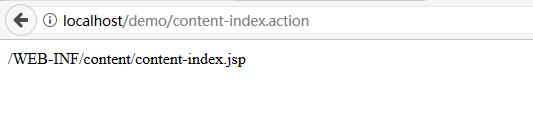
　　3.访问content-index.jsp

http://localhost/demo/content-index.action

　　4.访问project-index

http://localhost/demo/project/project-index.action

Java EE之Struts2路径访问小结的更多相关文章

  1. Java EE 编程中路径

    版权声明:未经博主允许,不得转载 首先我们要限定一个范围,是一个项目,或是以个访问地址..就先以一个项目为限定的范围 前述: 学过物理学的都知道相对运动和绝对运动, 虽然是相似的概念,但这里的要简单得 ...

  2. Java Web开发中路径问题小结

     Java Web开发中,路径问题是个挺麻烦的问题,本文小结了几个常见的路径问题,希望能对各位读者有所帮助. (1) Web开发中路径的几个基本概念 假设在浏览器中访问了如下的页面,如图1所示: 图1 ...

  3. java框架之Struts2(2)-访问Servlet API及请求数据封装

    准备 为后面测试示例编写代码及配置如下: package com.zze.bean; import java.util.Date; public class User { private String ...

  4. Java EE之Struts2异常[No mapping found for dependency [type=java.lang.String, name='actionPackages'#java.lang.RuntimeException]【摘抄】

    本博文摘自:http://www.blogjava.net/nkjava/archive/2009/03/29/262705.html 出现这个问题,可能是添加了struts2-codebehind包 ...

  5. Java Web开发中路径问题小结（getRequestUrl getContextUrl getServletUrl)

    看以博客感觉不错,分享一下http://www.cnblogs.com/tianguook/archive/2012/08/31/2665755.html (1) Web开发中路径的几个基本概念 假设 ...

  6. Java Web 开发中路径相关问题小结

    Java Web开发中路径问题小结 (1) Web开发中路径的几个基本概念 假设在浏览器中访问了如下的页面,如图1所示: 图1 Eclipse中目录结构如图2所示: 图2 那么针对这个站点的几个基本概 ...

  7. Struts2之访问路径

    上一篇已经和大家分享了关于Struts2命名空间和Action的三种创建方式,本篇我们接着命名空间的内容,来一起探讨一下关于Struts2的访问路径问题,何为访问路径,就是指当我们在浏览器输入地址,点 ...

  8. Java EE中的容器和注入分析，历史与未来

    Java EE中的容器和注入分析,历史与未来 java中的容器 java中的注入 容器和注入的历史和展望 一.java中的容器 java EE中的注入,使我们定义的对象能够获取对资源和其他依赖项的引用 ...

  9. java.lang.ClassNotFoundException: org.apache.struts2.dispatcher.ng.filter.StrutsPrepareAndExecuteFilter /struts2.1.3以前版本和之后版本区别/新版Eclipse找不到Java EE Module Dependencies选项

    严重: Exception starting filter struts2java.lang.ClassNotFoundException: org.apache.struts2.dispatcher ...

随机推荐

  1. HashMap, HashTable，HashSet,TreeMap 的时间复杂度

    hashSet,hashtable,hashMap 都是基于散列函数, 时间复杂度 O(1) 但是如果太差的话是O(n) TreeSet==>O(log(n))==> 基于树的搜索,只需要 ...

  2. cordic——sincos

    phase format :scaled radians,归化到多少pi roundmode :nearest even 近似值 coarse rotation: selected-pi——pi.no ...

  3. BZOJ1299[LLH邀请赛]巧克力棒——Nim游戏+搜索

    题目描述 TBL和X用巧克力棒玩游戏.每次一人可以从盒子里取出若干条巧克力棒,或是将一根取出的巧克力棒吃掉正整数长度.TBL先手两人轮流,无法操作的人输. 他们以最佳策略一共进行了10轮(每次一盒). ...

  4. Codeforces Round #337 (Div. 2) B. Vika and Squares

    B. Vika and Squares time limit per test 2 seconds memory limit per test 256 megabytes input standard ...

  5. MT【24】一道五次方程的求根题

    解答: 评:一般的五次及以上的多项式方程是无根式解的,只能用计算机去精确到某某位.但是特殊的比如$x^5=1$显然有根式解,本题就是一个不平凡的特殊的例子,这里的代换用于求解三次方程的求根过程是一样的 ...

  6. 自学Zabbix3.12.5-动作Action-Condition配置

    点击返回:自学Zabbix之路 点击返回:自学Zabbix4.0之路 点击返回:自学zabbix集锦 3.12.5 自学Zabbix3.12.5-动作Action-Condition配置 报警,肯定是 ...

  7. 【BZOJ1998】[HNOI2010]物品调度（并查集，模拟）

    [BZOJ1998][HNOI2010]物品调度(并查集,模拟) 题面 BZOJ,为啥这题都是权限题啊? 洛谷 题解 先不管\(0\)位置是个空,把它也看成一个箱子.那么最终的答案显然和置换循环节的个 ...

  8. emWin 之 WM_SetCallback 创建回调函数

    @2018-7-11 [小记] emWin 通过函数 WM_SetCallback ( )  自定义回调函数 > 下段代码就是通过 MESSAGEBOX 控件的 OK 按键实现删除信息框的对话框 ...

  9. AT1219 歴史の研究 解题报告

    AT1219 歴史の研究 题意 给定一个长为\(n\)的序列\(\{a\}\),询问区间\(a*cnt_a\)的最大值,即某个值乘上出现次数 回退莫队板子 只右移右指针和左指针每次回到块结尾即可. C ...

  10. 【POJ1015】Jury compromise 多个费用的背包

    这是一道比较综合的动态规划问题. 首先,根据题目中的从N个人中选出M个人,并且要使得某个目标函数最优,可以想到是背包问题,且因为要取出M个人,人数也应该作为背包体积的一个维度. 其次,要求输出路径,因 ...