BFS广度优先 vs DFS深度优先 for Binary Tree

https://www.geeksforgeeks.org/bfs-vs-dfs-binary-tree/

What are BFS and DFS for Binary Tree?
A Tree is typically traversed in two ways:

• Breadth First Traversal (Or Level Order Traversal)
• Depth First Traversals
  • Inorder Traversal (Left-Root-Right)
  • Preorder Traversal (Root-Left-Right)
  • Postorder Traversal (Left-Right-Root)

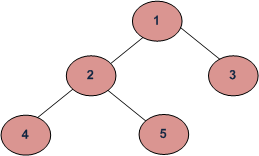
BFS and DFSs of above Tree

Breadth First Traversal : 1 2 3 4 5

Depth First Traversals:
      Preorder Traversal : 1 2 4 5 3
      Inorder Traversal  :  4 2 5 1 3
      Postorder Traversal : 4 5 2 3 1

Why do we care?
There are many tree questions that can be solved using any of the above four traversals. Examples of such questions are size, maximum, minimum, print left view, etc.

Is there any difference in terms of Time Complexity?
All four traversals require O(n) time as they visit every node exactly once.

Is there any difference in terms of Extra Space?
There is difference in terms of extra space required.

1. Extra Space required for Level Order Traversal is O(w) where w is maximum width of Binary Tree. In level order traversal, queue one by one stores nodes of different level.
2. Extra Space required for Depth First Traversals is O(h) where h is maximum height of Binary Tree. In Depth First Traversals, stack (or function call stack) stores all ancestors of a node.

Maximum Width of a Binary Tree at depth (or height) h can be 2^h where h starts from 0. So the maximum number of nodes can be at the last level. And worst case occurs when Binary Tree is a perfect Binary Tree with numbers of nodes like 1, 3, 7, 15, …etc. In worst case, value of 2^h is Ceil(n/2).

Height for a Balanced Binary Tree is O(Log n). Worst case occurs for skewed歪斜的 tree and worst case height becomes O(n).

So in worst case extra space required is O(n) for both. But worst cases occur for different types of trees.

It is evident from above points that extra space required for Level order traversal is likely to be more when tree is more balanced and extra space for Depth First Traversal is likely to be more when tree is less balanced.

How to Pick One?

1. Extra Space can be one factor (Explained above)
2. Depth First Traversals are typically recursive and recursive code requires function call overheads.
3. The most important points is, BFS starts visiting nodes from root while DFS starts visiting nodes from leaves. So if our problem is to search something that is more likely to closer to root, we would prefer BFS. And if the target node is close to a leaf, we would prefer DFS.

Exercise:
Which traversal should be used to print leaves of Binary Tree and why?
Which traversal should be used to print nodes at k’th level where k is much less than total number of levels?

This article is contributed by Dheeraj Gupta. This
Please write comments if you find anything incorrect, or you want to
share more information about the topic discussed above

二叉树的C#定义

public class TreeNode
    {
        public int val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(int x)
        {
            val = x;
        }
    }

广度优先的遍历C#实现

 public IList<IList<int>> LevelOrder(TreeNode root)
        {
            IList<IList<int>> result = new List<IList<int>>();
            Queue<TreeNode> queue=new Queue<TreeNode>();
            Enqueue(queue, root);
            while (queue.Count > )
            {
                var node = queue.Dequeue();
                Console.WriteLine(node.val);
                Output.WriteLine(node.val.ToString());
                Enqueue(queue, node.left);
                Enqueue(queue, node.right);
            }

            return result;
        }

        private void Enqueue(Queue<TreeNode> tempQueue, TreeNode node)
        {
            if (node != null)
            {
                tempQueue.Enqueue(node);
            }
        }