爬格子问题（经典强化学习问题） Sarsa 与 Q-Learning 的区别
SARSA v.s. Q-learning
爬格子问题，是典型的经典强化学习问题。
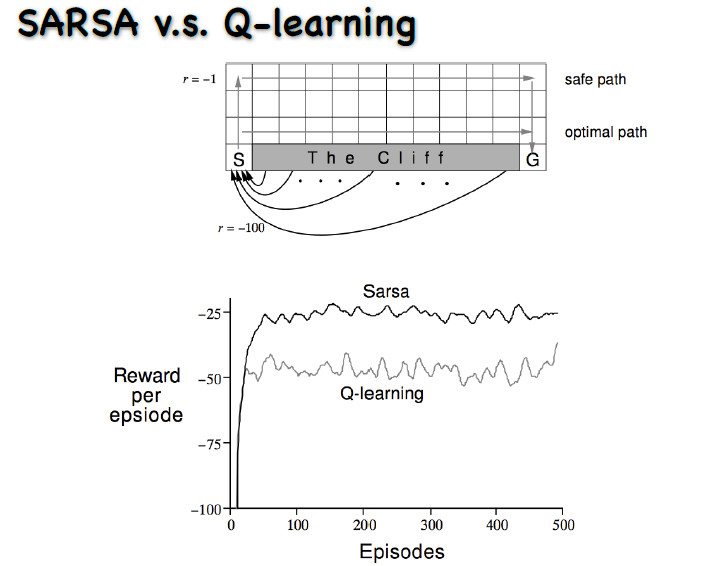
动作是上下左右的走，每走一步就会有一个-1的奖赏。从初始状态走到最终的状态，要走最短的路才能使奖赏最大。图中有一个悬崖，一旦走到悬崖奖赏会极小，而且还要再退回这个初始状态。
个人编写代码如下：
#encoding:UTF-8
#!/usr/bin/env python3 import math
import random
import matplotlib.pyplot as plt #动作的选择为上，下，左, 右
actions=["up", "down", "left", "right"] #坐标x的范围
x_scope=4 #坐标y的范围
y_scope=12 #greedy策略的探索因子(初始值)
epsilon_start=0.4
epsilon_final=0.01 #累积奖赏的折扣因子
discount_factor=0.99 #TD error的学习率
learning_rate=0.1 #动作值的字典
q_value=dict() #回合数
episodes=500 def calc_epsilon(t, epsilon_start=epsilon_start,
epsilon_final=epsilon_final, epsilon_decay=episodes):
if t<500:
epsilon = epsilon_final + (epsilon_start - epsilon_final) \
* math.exp(-1. * t / epsilon_decay)
else:
epsilon=0.0
return epsilon #动作值字典初始化
def q_value_init():
q_value.clear()
for i in range(x_scope):
for j in range(y_scope):
#状态坐标
state=(i, j)
for action in actions:
q_value[(state, action)]=0 #当前状态选择动作后的下一状态及其奖励
def state_reward_transition(state, action):
next_x, next_y=state
if action=="up":
next_x=state[0]-1
elif action=="down":
next_x=state[0]+1
elif action=="left":
next_y=state[1]-1
else:
next_y=state[1]+1 if next_x<0 or next_x>(x_scope-1) or next_y<0 or next_y>(y_scope-1):
next_state=state
reward=-1
return next_state, reward if next_x==0 and 0<next_y<(y_scope-1):
next_state=(0, 0)
reward=-100
return next_state, reward next_state=(next_x, next_y)
reward=-1
return next_state, reward #最大动作值选择法
def max_action(state):
q_value_list=[]
for action in actions:
q_value_list.append((q_value[(state, action)], action))
random.shuffle(q_value_list) action=max(q_value_list)[-1]
return action #greedy策略动作选择法
def greedy_action(state):
q_value_list=[]
for action in actions:
q_value_list.append((q_value[(state, action)], action))
random.shuffle(q_value_list) if random.random()>epsilon:
action=max(q_value_list)[-1]
else:
action=random.choice(q_value_list)[-1]
return action #sarsa策略
def sarsa(state):
#选择当前状态的动作
action=greedy_action(state)
next_state, reward=state_reward_transition(state, action) #选择下一状态的动作
next_action=greedy_action(next_state) #对当前动作值的估计
estimate=reward+discount_factor*q_value[(next_state, next_action)] #TD error
error=estimate-q_value[(state, action)] #学习到的新当前动作值
q_value[(state, action)]+=learning_rate*error
return next_state, reward def q_learning(state):
#选择当前状态的动作
action=greedy_action(state)
next_state, reward=state_reward_transition(state, action) #选择下一状态的动作
next_action=max_action(next_state) #对当前动作值的估计
estimate=reward+discount_factor*q_value[(next_state, next_action)]
#TD error
error=estimate-q_value[(state, action)]
#学习到的新当前动作值
q_value[(state, action)]+=learning_rate*error
return next_state, reward if __name__=="__main__":
reward_list_1=[]
q_value_init()
for episode in range(episodes+100):
reward_sum=0
state=(0, 0)
epsilon=calc_epsilon(episode)
while state!=(x_scope-1, y_scope-1):
state, reward=sarsa(state)
reward_sum+=reward
reward_list_1.append(reward_sum) for i in range(x_scope):
for j in range(y_scope):
print("-"*20)
for action in actions:
print( "("+str(i)+", "+str(j)+") : "+action+" "+str(q_value[((i, j), action)])) plt.subplot(211)
plt.plot(reward_list_1, label="sarsa")
plt.legend(loc = 0)
plt.xlabel('episode')
plt.ylabel('reward sum per episode')
plt.xlim(0,600)
plt.ylim(-2000, 0)
plt.title("sarsa") reward_list_2=[]
q_value_init()
for episode in range(episodes+100):
reward_sum=0
state=(0, 0)
epsilon=calc_epsilon(episode)
while state!=(x_scope-1, y_scope-1):
state, reward=q_learning(state)
reward_sum+=reward
reward_list_2.append(reward_sum) for i in range(x_scope):
for j in range(y_scope):
print("-"*20)
for action in actions:
print( "("+str(i)+", "+str(j)+") : "+action+" "+str(q_value[((i, j), action)])) plt.subplot(212)
plt.plot(reward_list_2, label="q-learning")
plt.legend(loc = 0)
plt.xlabel('episode')
plt.ylabel('reward sum per episode')
plt.xlim(0,600)
plt.ylim(-2000, 0)
plt.title("q-learning")
plt.show() plt.plot(reward_list_1, label="sarsa")
plt.plot(reward_list_2, label="q-learning")
plt.legend(loc = 0)
plt.xlabel('episode')
plt.ylabel('reward sum per episode')
plt.xlim(0,600)
plt.ylim(-2000, 0)
plt.title("SARSA & Q-LEARNING")
plt.show()
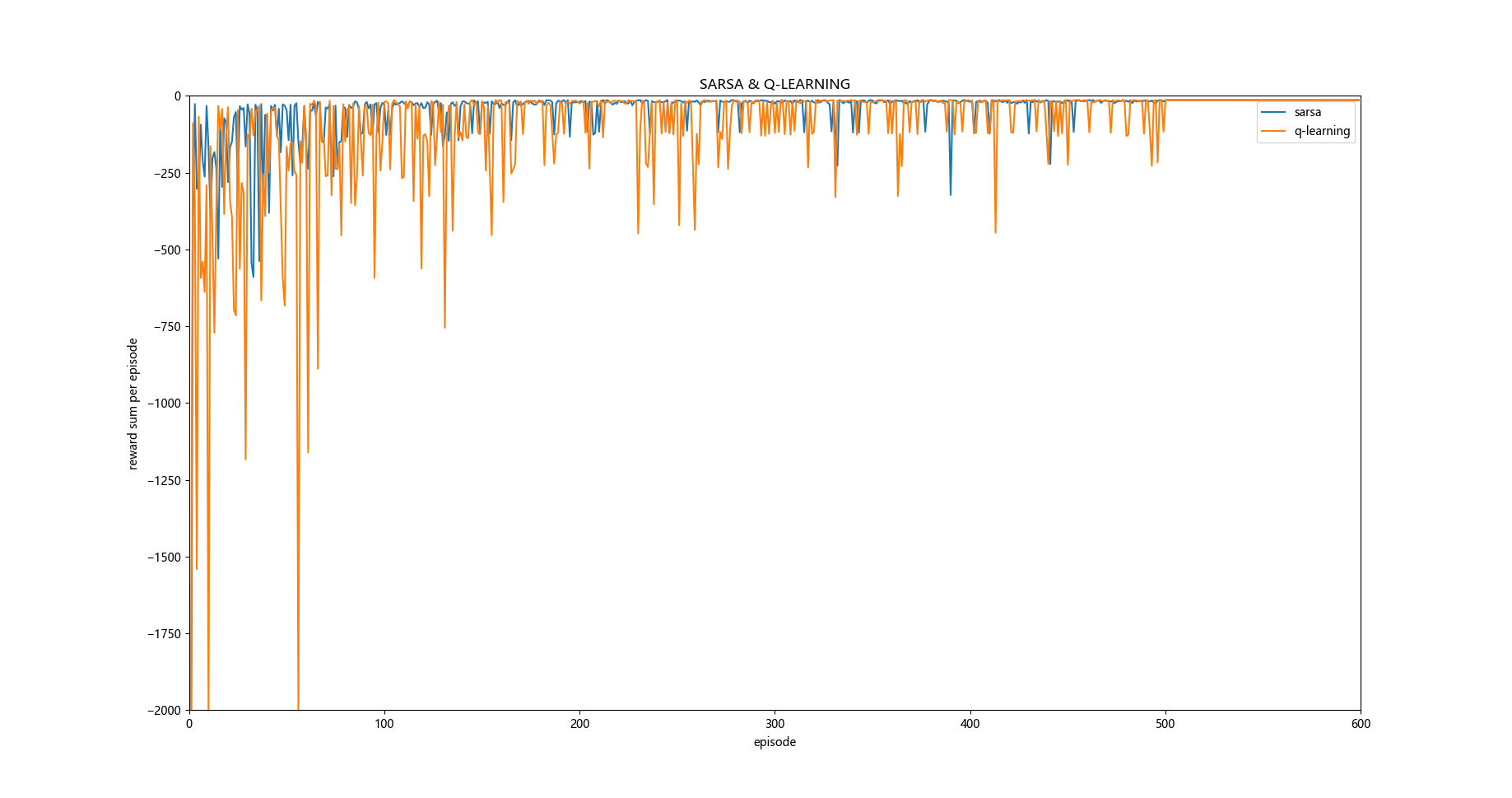
从自我编写的代码运行的程序效果和原题目给出的效果图来看还是有些差距的，个人感觉这个应该是超参数设置的问题。
如：学习率， greedy策略的epsilon设置等。
不过有一点是相似的，那就是q-learning学习的过程中奖励值一般要小于sarsa学习方法。
对于为什么在这个问题中 q-learning的学习过程中奖励值的累积和要普遍小于sarsa方法，个人观点是按照原题目给出的效果图分析是因为sarsa对策略的探索更加高效， 更有可能走optimal path, 而q-learning 对下一状态q值的探索是直接用最大值来估计的，所以更有可能走safe path路线。
=================================================================
如果这个问题中没有悬崖的话，那么运行结果如何呢？
代码如下：
#encoding:UTF-8
#!/usr/bin/env python3 import math
import random
import matplotlib.pyplot as plt #动作的选择为上，下，左, 右
actions=["up", "down", "left", "right"] #坐标x的范围
x_scope=4 #坐标y的范围
y_scope=12 #greedy策略的探索因子(初始值)
epsilon_start=0.4
epsilon_final=0.01 #累积奖赏的折扣因子
discount_factor=0.99 #TD error的学习率
learning_rate=0.1 #动作值的字典
q_value=dict() #回合数
episodes=500 def calc_epsilon(t, epsilon_start=epsilon_start,
epsilon_final=epsilon_final, epsilon_decay=episodes):
if t<500:
epsilon = epsilon_final + (epsilon_start - epsilon_final) \
* math.exp(-1. * t / epsilon_decay)
else:
epsilon=0.0
return epsilon #动作值字典初始化
def q_value_init():
q_value.clear()
for i in range(x_scope):
for j in range(y_scope):
#状态坐标
state=(i, j)
for action in actions:
q_value[(state, action)]=0 #当前状态选择动作后的下一状态及其奖励
def state_reward_transition(state, action):
next_x, next_y=state
if action=="up":
next_x=state[0]-1
elif action=="down":
next_x=state[0]+1
elif action=="left":
next_y=state[1]-1
else:
next_y=state[1]+1 if next_x<0 or next_x>(x_scope-1) or next_y<0 or next_y>(y_scope-1):
next_state=state
reward=-1
return next_state, reward """
if next_x==0 and 0<next_y<(y_scope-1):
next_state=(0, 0)
reward=-100
return next_state, reward
""" next_state=(next_x, next_y)
reward=-1
return next_state, reward #最大动作值选择法
def max_action(state):
q_value_list=[]
for action in actions:
q_value_list.append((q_value[(state, action)], action))
random.shuffle(q_value_list) action=max(q_value_list)[-1]
return action #greedy策略动作选择法
def greedy_action(state):
q_value_list=[]
for action in actions:
q_value_list.append((q_value[(state, action)], action))
random.shuffle(q_value_list) if random.random()>epsilon:
action=max(q_value_list)[-1]
else:
action=random.choice(q_value_list)[-1]
return action #sarsa策略
def sarsa(state):
#选择当前状态的动作
action=greedy_action(state)
next_state, reward=state_reward_transition(state, action) #选择下一状态的动作
next_action=greedy_action(next_state) #对当前动作值的估计
estimate=reward+discount_factor*q_value[(next_state, next_action)] #TD error
error=estimate-q_value[(state, action)] #学习到的新当前动作值
q_value[(state, action)]+=learning_rate*error
return next_state, reward def q_learning(state):
#选择当前状态的动作
action=greedy_action(state)
next_state, reward=state_reward_transition(state, action) #选择下一状态的动作
next_action=max_action(next_state) #对当前动作值的估计
estimate=reward+discount_factor*q_value[(next_state, next_action)]
#TD error
error=estimate-q_value[(state, action)]
#学习到的新当前动作值
q_value[(state, action)]+=learning_rate*error
return next_state, reward if __name__=="__main__":
reward_list_1=[]
q_value_init()
for episode in range(episodes+100):
reward_sum=0
state=(0, 0)
epsilon=calc_epsilon(episode)
while state!=(x_scope-1, y_scope-1):
state, reward=sarsa(state)
reward_sum+=reward
reward_list_1.append(reward_sum) for i in range(x_scope):
for j in range(y_scope):
print("-"*20)
for action in actions:
print( "("+str(i)+", "+str(j)+") : "+action+" "+str(q_value[((i, j), action)])) plt.subplot(211)
plt.plot(reward_list_1, label="sarsa")
plt.legend(loc = 0)
plt.xlabel('episode')
plt.ylabel('reward sum per episode')
plt.xlim(0,600)
plt.ylim(-2000, 0)
plt.title("sarsa") reward_list_2=[]
q_value_init()
for episode in range(episodes+100):
reward_sum=0
state=(0, 0)
epsilon=calc_epsilon(episode)
while state!=(x_scope-1, y_scope-1):
state, reward=q_learning(state)
reward_sum+=reward
reward_list_2.append(reward_sum) for i in range(x_scope):
for j in range(y_scope):
print("-"*20)
for action in actions:
print( "("+str(i)+", "+str(j)+") : "+action+" "+str(q_value[((i, j), action)])) plt.subplot(212)
plt.plot(reward_list_2, label="q-learning")
plt.legend(loc = 0)
plt.xlabel('episode')
plt.ylabel('reward sum per episode')
plt.xlim(0,600)
plt.ylim(-2000, 0)
plt.title("q-learning")
plt.show() plt.plot(reward_list_1, label="sarsa")
plt.plot(reward_list_2, label="q-learning")
plt.legend(loc = 0)
plt.xlabel('episode')
plt.ylabel('reward sum per episode')
plt.xlim(0,600)
plt.ylim(-2000, 0)
plt.title("SARSA & Q-LEARNING")
plt.show()
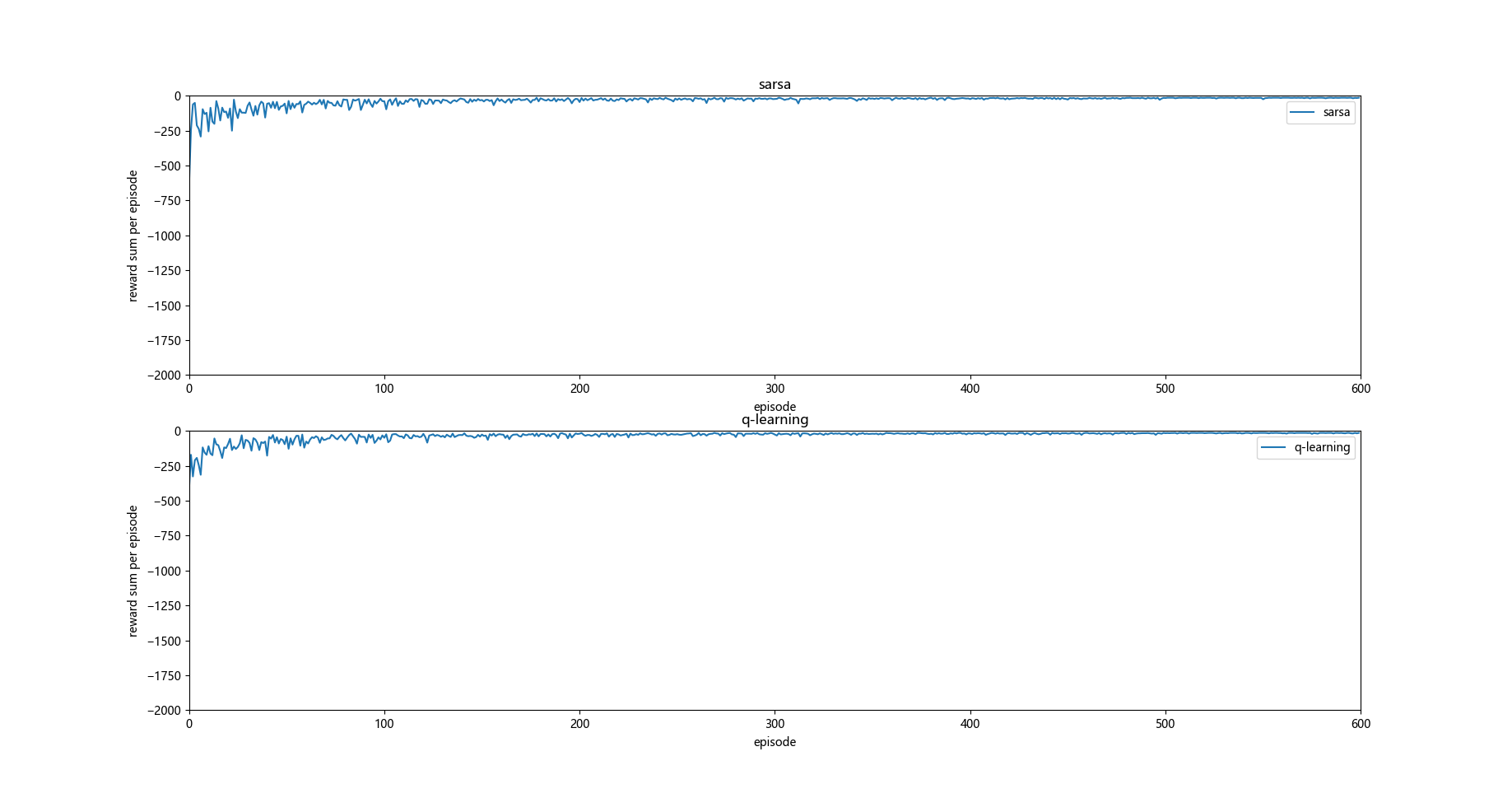
这时候发现如果没有悬崖的话 q-learning 和 sarsa 运行的效果大致相同。
个人观点：
如果按照原题目给出的效果图分析 q_learning 学习对惩罚项敏感，探索效率低于sarsa, 因为q_learning中对下一状态的q值采用max方法来估计，所以在算法运行过程中会尽量远离初步判断不好的选择，即选择safe path, 某种角度上来说也是其探索效率小于sarsa的一个结果。
按照原题目效果图分析并结合上图所示， S0状态是初始状态，在q_learning 算法初始时容易得出S1状态时right动作的q值较低的结论，原因是S2状态时up操作的q值较低，S3状态时q值较高，所以q_learning更倾向于在S1状态选择down操作。
但是依照个人所做实验的效果图分析，则和上面的分析不太一样：
那就是 q_learning更偏向于探索optimal path, 而sarsa更倾向于探索safe path, 因为正是因为q_learning 探索optimal path才会有多次掉入悬崖的情况，而sarsa掉入悬崖次数较少则说明其更倾向于探索safe path 。
爬格子问题（经典强化学习问题） Sarsa 与 Q-Learning 的区别的更多相关文章
- 强化学习系列之:Deep Q Network (DQN)
文章目录 [隐藏] 1. 强化学习和深度学习结合 2. Deep Q Network (DQN) 算法 3. 后续发展 3.1 Double DQN 3.2 Prioritized Replay 3. ...
- 强化学习 - Q-learning Sarsa 和 DQN 的理解
本文用于基本入门理解. 强化学习的基本理论 : R, S, A 这些就不说了. 先设想两个场景: 一. 1个 5x5 的 格子图, 里面有一个目标点, 2个死亡点二. 一个迷宫, 一个出发点, ...
- 强化学习之Sarsa （时间差分学习）
上篇文章讲到Q-learning, Sarsa与Q-learning的在决策上是完全相同的,不同之处在于学习的方式上 这次我们用openai gym的Taxi来做演示 Taxi是一个出租车的游戏,把顾 ...
- 深度强化学习：入门(Deep Reinforcement Learning: Scratching the surface)
RL的方案 两个主要对象:Agent和Environment Agent观察Environment,做出Action,这个Action会对Environment造成一定影响和改变,继而Agent会从新 ...
- 【转载】 “强化学习之父”萨顿：预测学习马上要火，AI将帮我们理解人类意识
原文地址: https://yq.aliyun.com/articles/400366 本文来自AI新媒体量子位(QbitAI) ------------------------------- ...
- ICML 2018 | 从强化学习到生成模型：40篇值得一读的论文
https://blog.csdn.net/y80gDg1/article/details/81463731 感谢阅读腾讯AI Lab微信号第34篇文章.当地时间 7 月 10-15 日,第 35 届 ...
- (转) 深度强化学习综述：从AlphaGo背后的力量到学习资源分享（附论文）
本文转自:http://mp.weixin.qq.com/s/aAHbybdbs_GtY8OyU6h5WA 专题 | 深度强化学习综述:从AlphaGo背后的力量到学习资源分享(附论文) 原创 201 ...
- 强化学习9-Deep Q Learning
之前讲到Sarsa和Q Learning都不太适合解决大规模问题,为什么呢? 因为传统的强化学习都有一张Q表,这张Q表记录了每个状态下,每个动作的q值,但是现实问题往往极其复杂,其状态非常多,甚至是连 ...
- 强化学习(Reinfment Learning) 简介
本文内容来自以下两个链接: https://morvanzhou.github.io/tutorials/machine-learning/reinforcement-learning/ https: ...
随机推荐
- SpringMvc4.2.5 零配置出现 No mapping found for HTTP request with URI（转）
原文地址:SpringMvc4.2.5 零配置出现 No mapping found for HTTP request with URI 采用 spring 零配置,参考 http://hanqunf ...
- Mybatis 查询tinyint(1)的数据库字段时会自动转换成boolean类型
解决方案:将字段的tinyint(1)变成tinyint(2)
- Lunx下 怎样启动和关闭oracle数据库
1.因为oracle运行在Linux系统下,首先,要连接Linux系统 2.切换到oracle安装用户下. 我的是 ora12. 3.运行oracle的环境变量, 以便输入相关命令. 4.进入orac ...
- 【转】Code First 属性详解
下面解释每个配置的作用 Table :用于指定生成表的表名.架构信息. Column :用于指定生成数据表的列信息,如列名.数据类型.顺序等. Key :用于指定任何名称的属性作为主键列并且默认将此列 ...
- python 自然语言处理（三）____条件频率分布
条件频率分布就是频率分布的集合,每个频率分布有一个不同的“条件”,这个条件通常是文本的类别.当语料文本分为几类(文体,主题,作者等)时,可以计算每个类别独立的频率分布,这样,就可以通过条件频率分布研究 ...
- unity3D开发的程序发布到Android平台上进行运行测试的详细步骤
第一步 下载安装JDK 和SDK 1.需要配置java环境.点击链接进入ava的配置的方法:http://www.cnblogs.com/Study088/p/7496158.html 2.下载 ...
- MySQL 占用cpu 100%
目前的线上数据库,分为主从两个库,从库用来做比较耗时的数据统计分析. 今天top了一下从库服务器,发现mysqld 在很长一段时间都占用105% cpu,一开始以为是从库在处理主库的binlog. 两 ...
- C语言转义字符'\'
body, table{font-family: 微软雅黑; font-size: 13.5pt} table{border-collapse: collapse; border: solid gra ...
- 类型重命名 typedef
所谓数据重命名就是给数据类型起一个新的名字,比如int 这个数据类型,可以给他起一个新的名字叫 my int.他俩的用法.特点.属性等是一模一样,仅仅名字不同而已. 作用:1,增加代码的可读性.2,让 ...
- 进程中的Manager(),实现多进程的数据共享与传递
__author__ = "Alex Li" from multiprocessing import Process, Managerimport osdef f(d, l): d ...