AI之旅（4）：初识逻辑回归

前置知识

  求导

知识地图

  逻辑回归是用于分类的算法，最小的分类问题是二元分类。猫与狗，好与坏，正常与异常。掌握逻辑回归的重点，是理解S型函数在算法中所发挥的作用，以及相关推导过程。

从一个例子开始

  假设我们是信贷工作人员，有一个关于客户记录的数据集。数据集中有两个特征，x1表示月收入金额，x2表示月还贷金额。y称为标签，其中y=1表示客户发生违约。

  我们的目标是挖掘出数据间可能存在的规律，建立相应的模型，用于对新客户进行预测。假设一个新客户的收入金额是5.0，还贷金额是2.7，请判断客户最可能属于的类别。

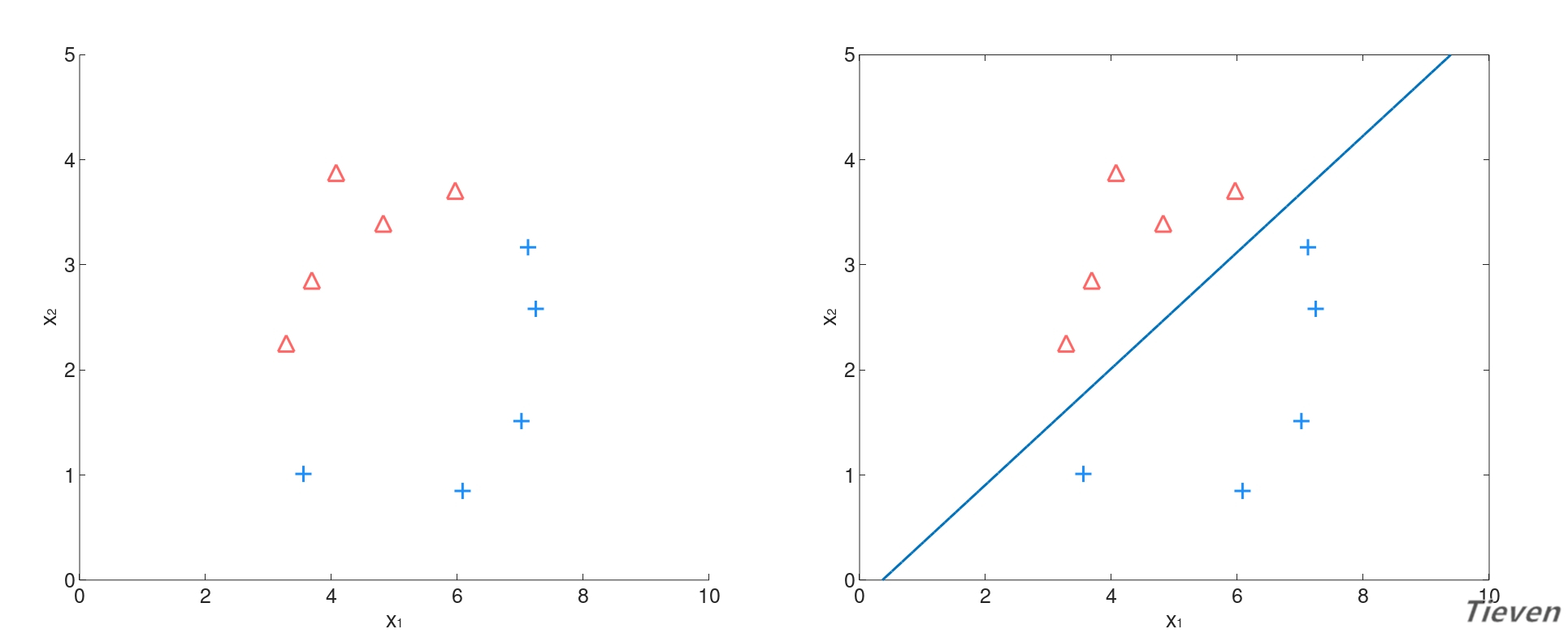
  图中三角形表示y=1的样本，十字表示y=0的样本。一般约定将关注的重点定义为y=1的类别，在这个问题中重点是寻找可能发生违约的客户，因此将违约客户定义为y=1。

  观察上图可以发现，似乎可以用一个边界将样本分为两类。于是问题转化为如何寻找到这样的边界，能够将全部样本正确地分离，或者将最多数量的样本正确地分离。

  记得在线性回归中，假设函数是如下形式：

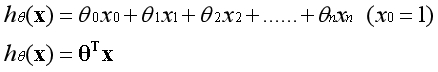
  以两个特征为例，这既可以表现为线性模型，对应的边界在空间中表现为一条直线：

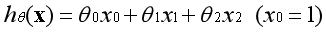
  通过添加高阶多项式，也可以表现为非线性模型，对应的边界在空间中表现为一条曲线：

  无论是线性模型还是非线性模型，从空间的角度看，模型的作用是将空间切成两部分。从方程的角度看，模型的作用是将一个样本映射为一个实数。用一条直线来举例：

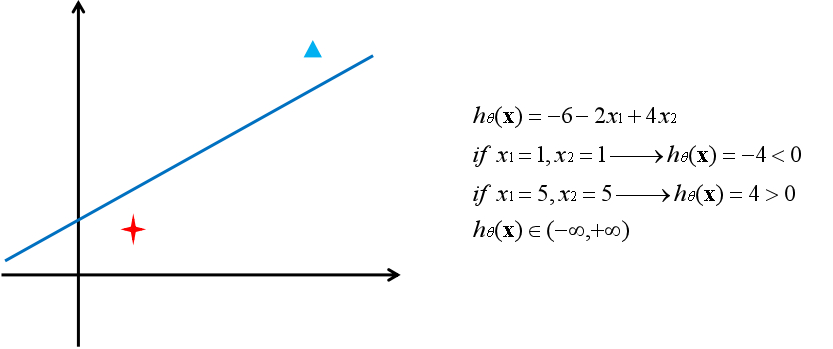
  现在的问题是这个实数的范围属于负无穷到正无穷，而通常是用概率的形式表示事物属于某一类别的可能性，因此还需要一个函数将实数映射到0和1之间。

S型函数

  想象一下这个函数应该具有的形状，当x越小时y越接近0，当x越大时y越接近1，这是一个S型的函数。S型函数有很多种，我们选择的是名为Sigmoid的函数，也叫逻辑函数。

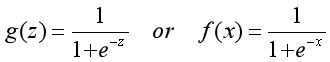
  因为特征是用x表示，为了与特征区别开，一般使用第一种形式来表示逻辑函数。函数对应的图像如下，注意当z等于0时，Sigmoid函数的值为0.5，这是概率中的分界点。

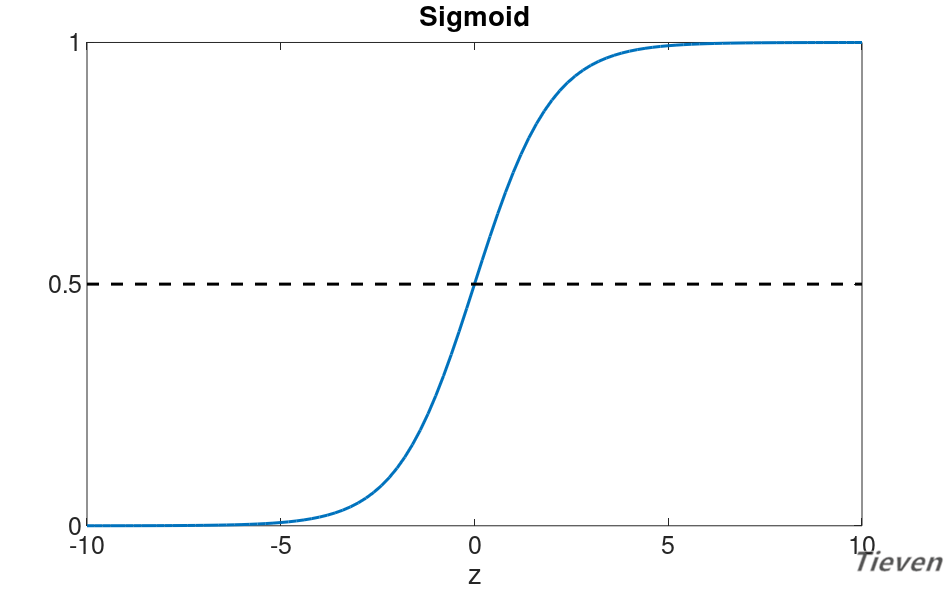
  Sigmoid函数基本性质：

  1，定义域：(-∞,+∞)；

  2，值域：(0,1)；

  3，函数在定义域内为连续和光滑的曲线；

  4，处处可导，导数为：g’(z)=g(z)(1-g(z))；

  Sigmoid导数推导过程：

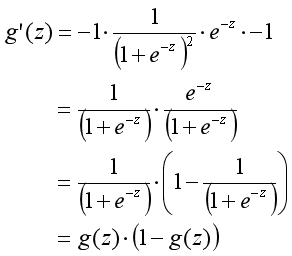
  线性回归的模型将样本映射为负无穷到正无穷间的实数，Sigmoid函数将该实数映射为0到1之间的数。两者结合使用，得到的数值可以表示样本属于某一类别的概率。

假设函数

  逻辑回归假设函数是在线性回归假设函数的基础上，再加上一个Sigmoid函数。所实现的作用是先将样本映射为一个实数，再将实数映射为一个概率，形式如下：

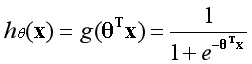
  一般表示概率是用如下形式表示，含义为在给定参数θ的情况下，当随机变量为x时，y的概率估计。

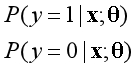
  因为是二元分类，显然如果一个样本预测为y=1的概率是0.7，相应的该样本预测为y=0的概率是0.3。在概率中以0.5作为分界点，假设函数所发挥的作用如下图所示：

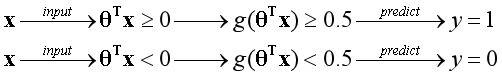
  逻辑回归算法的最终目的，是获得合适的参数θ，用结构图的形式表示如下：

代价函数

  因为逻辑回归的假设函数是非线性函数，样本都被压缩成0到1之间的数值，所以不适合用距离来衡量模型的准确性，我们需要构造一个新的代价函数。

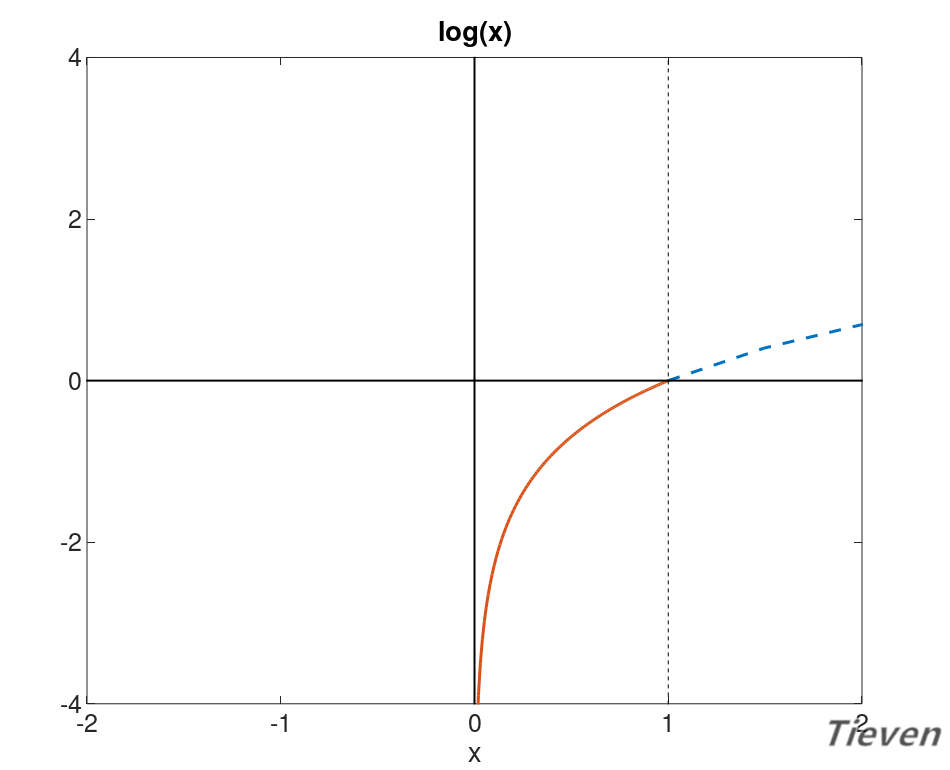
  上图是log(x)的图像，观察图像的趋势可以发现，当x接近1的时候，y接近0。当x接近0的时候，y接近负无穷。根据图像特性可以构造第一个代价函数。

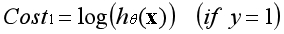
  当样本的类别为1时，若预测样本的类别接近1，说明预测准确，代价接近0；

  当样本的类别为1时，若预测样本的类别接近0，说明预测不准确，代价接近负无穷；

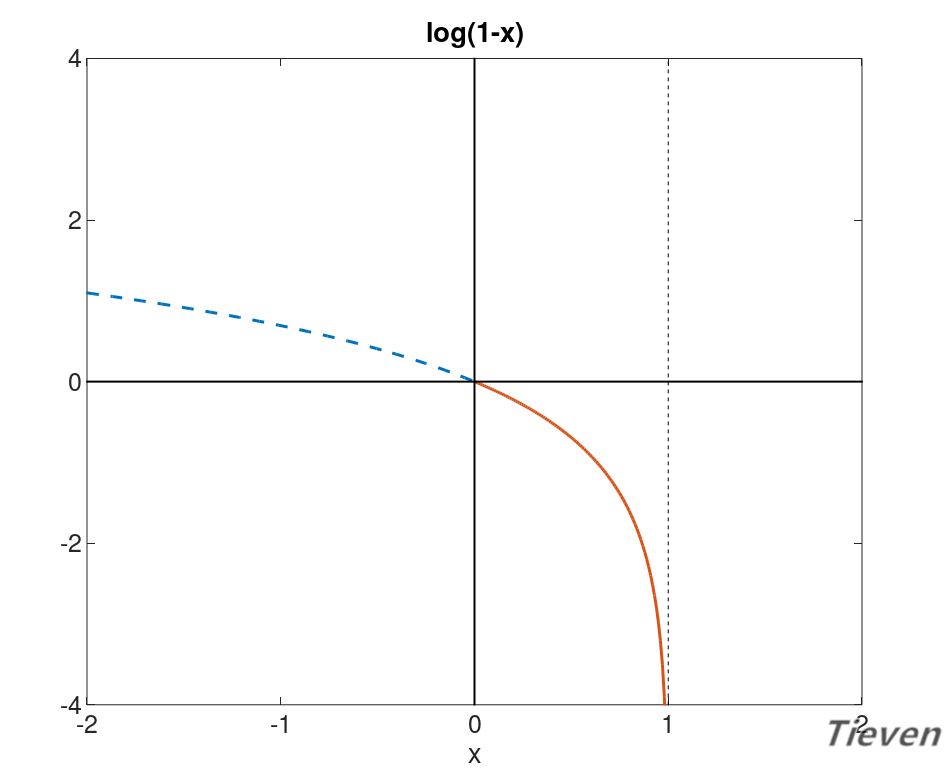
  上图是log(1-x)的图像，观察图像的趋势可以发现，当x接近0的时候，y接近0。当x接近1的时候，y接近负无穷。根据图像性质可以构造第二个代价函数。

  当样本的类别为0时，若预测样本的类别接近0，说明预测准确，代价接近0；

  当样本的类别为0时，若预测样本的类别接近1，说明预测不准确，代价接近负无穷；

  根据对数函数的图像性质，可以构造出评估模型准确性的代价函数。当样本类别为1时对应第一个代价函数，为0时对应第二个代价函数。能否将两个函数合并为一个函数呢？

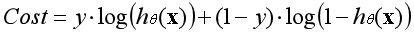
  因为y的取值只有1和0，当y等于1时函数第二部分消失，当y等于0时函数第一部分消失，这个函数包含了所有可能出现的四种情况。所以数据集的平均代价函数如下：

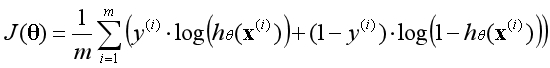
  注：这里的log函数特指e为底的对数；

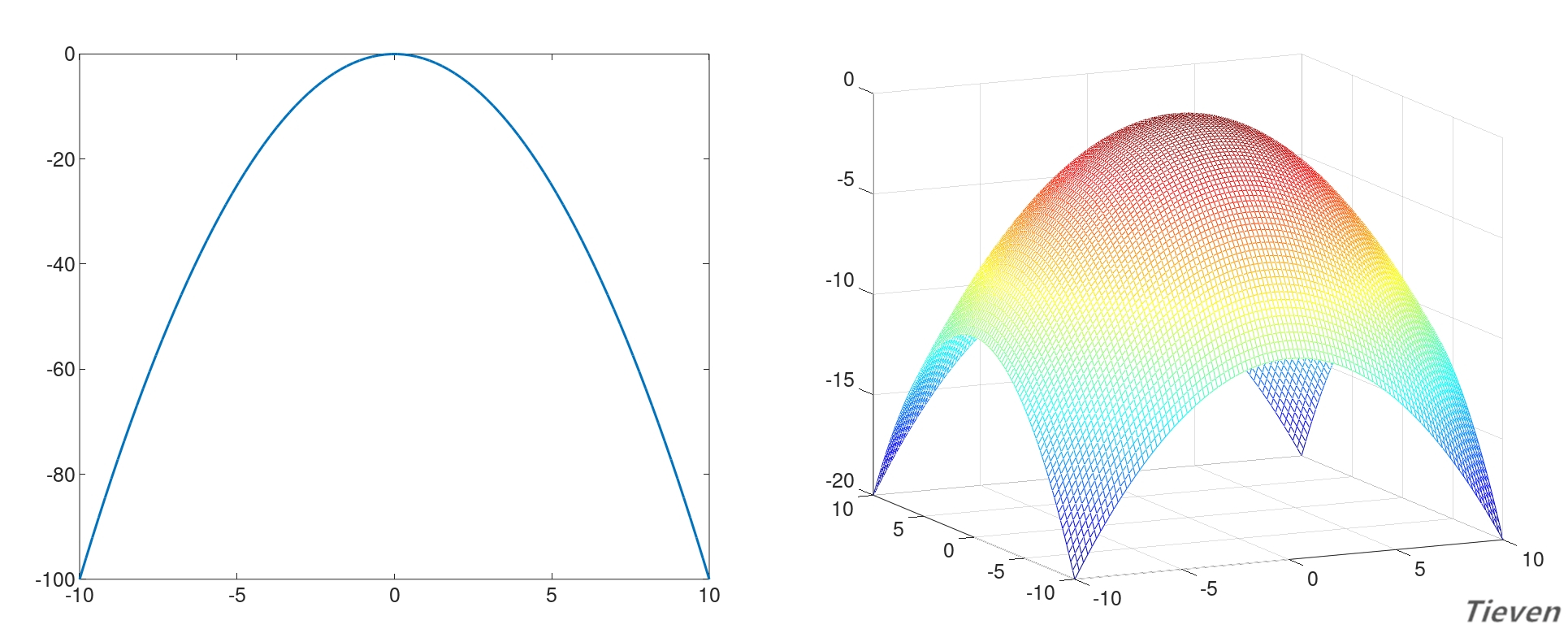
  所谓代价，是给予算法判断错误的惩罚。当预测准确时，代价接近0；当预测不准确时，代价接近负无穷。因此目标是将代价函数最大化，逻辑回归的代价函数有全局最优解。

代价函数的导数

  与线性回归类似，逻辑回归也是通过梯度更新的方法求最优解。首先要求出代价函数的偏导数，通过将其他变量视为常数，运用链式法则逐层求导，以下为推导过程：

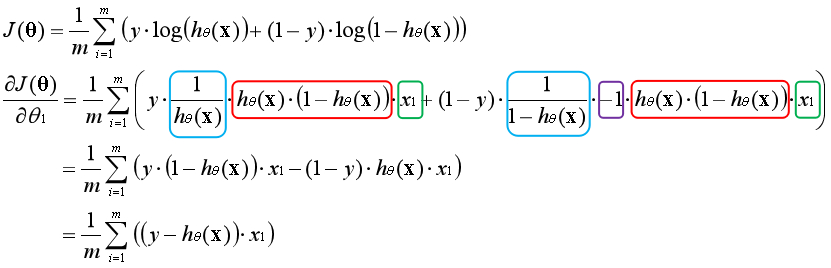
  第一层（蓝色）对e为底的对数求导，第二层（红色）对Sigmoid函数求导，第三层（绿色）对线性模型求导。

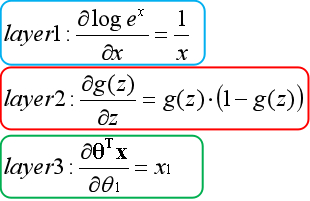
梯度上升

  梯度上升法是让参数向偏导数的同方向调整，反复迭代，逐步靠近全局最优点的方法。从直观上看参数从任意一个位置出发，总是一步步接近最高点的位置，如下图所示：

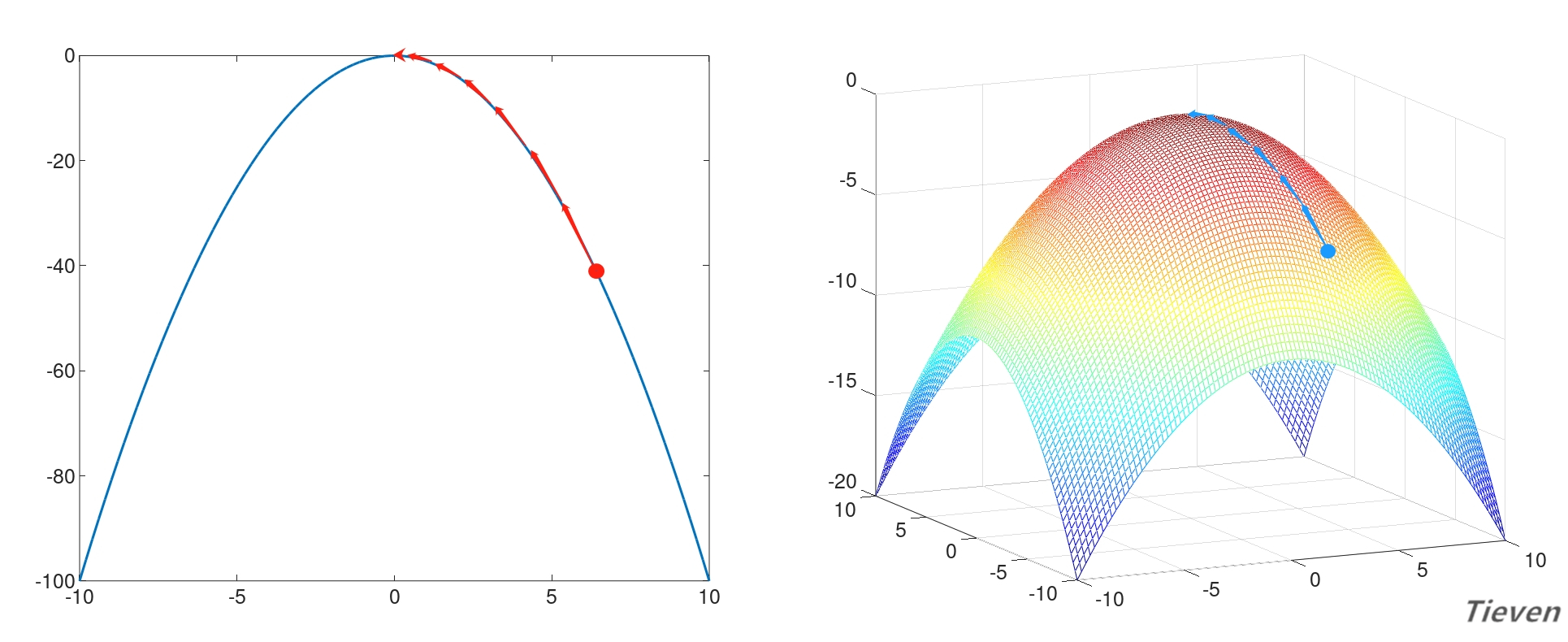
  梯度上升公式（示例）：

  注：α为学习率；

  注：n为特征的数量；

  在实际运用中参数θ必须同时更新，一次梯度上升指的是所有的参数运用旧的参数同时更新一次。不能先更新第一个参数，然后用更新后的第一个参数去更新第二个参数。

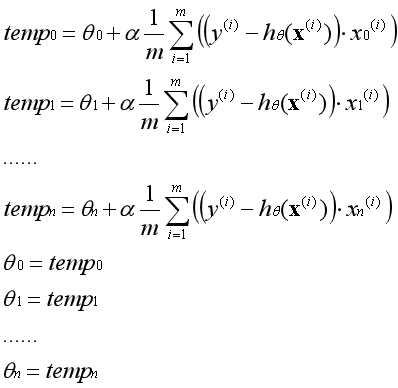
  下图为两个正常运行的梯度上升的代价函数图像：

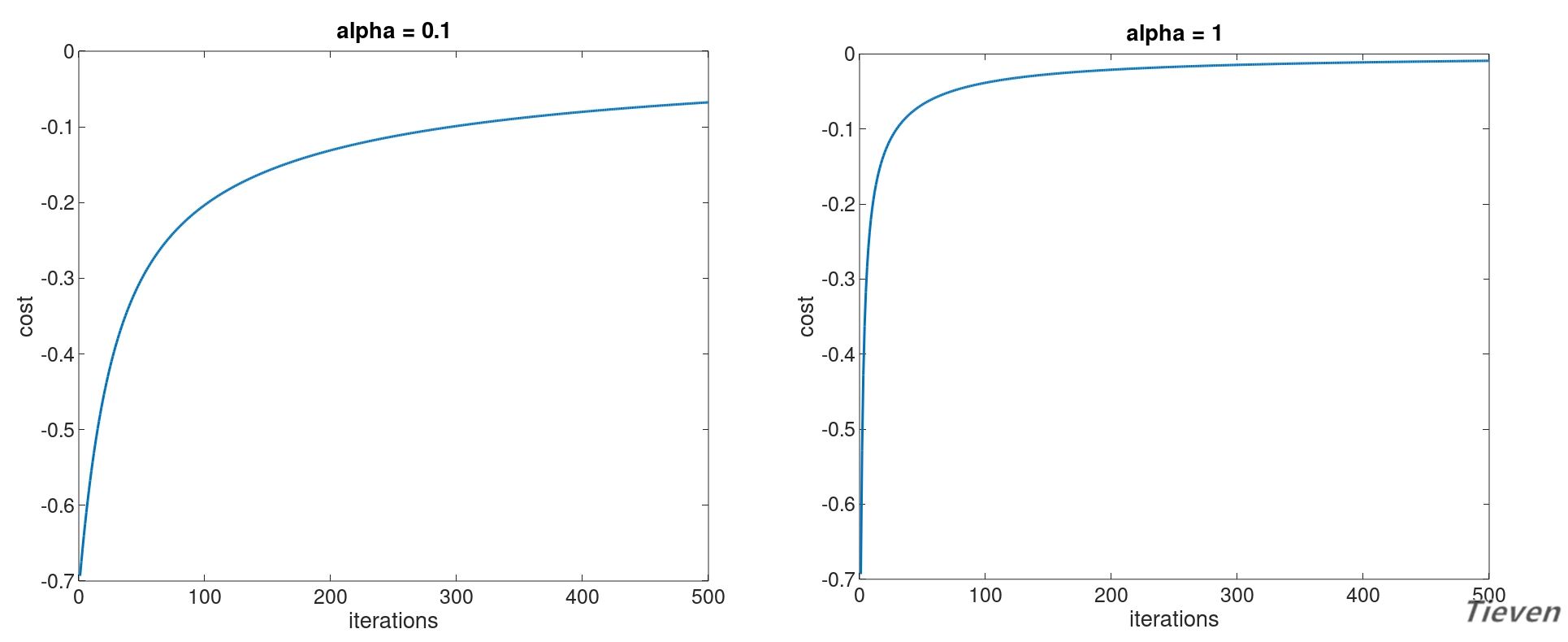
  对比线性回归中运用的梯度下降法，可以发现这两者本质上是同一种方法，都是通过对偏导数的反复更新逐步靠近全局最优点。

多元分类

  如果给出一个包含多个类别的数据集，如何用逻辑回归算法对其进行分类呢？我们可以将这个问题转化为多个独立的二元分类问题。

  将第一类视为正项，其他项视为负项，训练出第一个分类器；

  将第二类视为正项，其他项视为负项，训练出第二个分类器；

  将第三类视为正项，其他项视为负项，训练出第三个分类器；

  ......

  有了多个分类器以后，将要预测的新样本同时输入到多个分类器中，每个分类器会给出样本属于该类别的概率。哪一个类别的概率最高，就预测新样本属于哪一类。

向量化

  如果构建一个最小单位的逻辑回归模型，将梯度下降的方程展开后，经过适当的变换，会发现逻辑回归的梯度上升可以用一行代码表达。

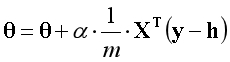
  注：X是样本构成的矩阵，矩阵规格为(m×n)；

  注：θ是参数构成的向量，向量规格为（n×1）；

  注：h是假设函数，h=g(Xθ)；

  注：g是Sigmoid函数；

  注：说明原理时向量的下标是从0开始，实际运用中向量的下标是从1开始；

总结

  逻辑回归是用于分类的算法，通过线性模型将样本映射为实数，通过Sigmoid函数将实数映射为概率，用概率衡量事物属于某一类别的可能性。这是逻辑回归的假设函数。

  根据对数函数的图像性质，构造出符合要求的代价函数，这个代价函数有全局最优解。通过梯度上升的方法反复迭代，得到代表全局最优解的参数θ。这是逻辑回归的实现方法。

  至此，我们掌握了两个基本的算法。线性回归可用于预测趋势，逻辑回归可用于判断类别。通过对这两个算法进行变换组合，可以构造出更强大的算法，比如神经网络。

  回到开头的例子，将这个小小的数据集扔到逻辑回归算法中学习后，可以预测新客户属于y=1的可能性约为85%。去寻找更多的数据集来实践吧，实践是记忆的最好方法。

非正规代码

版权声明

  1，本文为原创文章，未经作者授权禁止引用、复制、转载、摘编。

  2，对于有上述行为者，作者将保留追究其法律责任的权利。

Tieven

2019.1.7

tieven.it@gmail.com