O(n*logn)级别的算法之二（快速排序）的三种实现方法详解及其与归并排序的对比
一，单路快排
1.测试用例：
#ifndef INC_06_QUICK_SORT_DEAL_WITH_NEARLY_ORDERED_ARRAY_SORTTESTHELPER_H
#define INC_06_QUICK_SORT_DEAL_WITH_NEARLY_ORDERED_ARRAY_SORTTESTHELPER_H
#include <iostream>
#include <algorithm>
#include <string>
#include <ctime>
#include <cassert>
using namespace std;
namespace SortTestHelper {
// 生成有n个元素的随机数组,每个元素的随机范围为[rangeL, rangeR]
int *generateRandomArray(int n, int range_l, int range_r) {
int *arr = new int[n];
srand(time(NULL));
for (int i = ; i < n; i++)
arr[i] = rand() % (range_r - range_l + ) + range_l;
return arr;
}
// 生成一个近乎有序的数组
// 首先生成一个含有[0...n-1]的完全有序数组, 之后随机交换swapTimes对数据
// swapTimes定义了数组的无序程度
int *generateNearlyOrderedArray(int n, int swapTimes){
int *arr = new int[n];
for(int i = ; i < n ; i ++ )
arr[i] = i;
srand(time(NULL));
for( int i = ; i < swapTimes ; i ++ ){
int posx = rand()%n;
int posy = rand()%n;
swap( arr[posx] , arr[posy] );
}
return arr;
}
// 拷贝整型数组a中的所有元素到一个新的数组, 并返回新的数组
int *copyIntArray(int a[], int n){
int *arr = new int[n];
copy(a, a+n, arr);
return arr;
}
// 打印arr数组的所有内容
template<typename T>
void printArray(T arr[], int n) {
for (int i = ; i < n; i++)
cout << arr[i] << " ";
cout << endl; return;
}
// 判断arr数组是否有序
template<typename T>
bool isSorted(T arr[], int n) {
for (int i = ; i < n - ; i++)
if (arr[i] > arr[i + ])
return false;
return true;
}
// 测试sort排序算法排序arr数组所得到结果的正确性和算法运行时间
template<typename T>
void testSort(const string &sortName, void (*sort)(T[], int), T arr[], int n) {
clock_t startTime = clock();
sort(arr, n);
clock_t endTime = clock();
cout << sortName << " : " << double(endTime - startTime) / CLOCKS_PER_SEC << " s"<<endl;
assert(isSorted(arr, n));
return;
}
};
#endif
2.归并排序：
#ifndef INC_06_QUICK_SORT_DEAL_WITH_NEARLY_ORDERED_ARRAY_MERGESORT_H
#define INC_06_QUICK_SORT_DEAL_WITH_NEARLY_ORDERED_ARRAY_MERGESORT_H
#include <iostream>
#include <algorithm>
#include "InsertionSort.h"
using namespace std;
// 将arr[l...mid]和arr[mid+1...r]两部分进行归并
template<typename T>
void __merge(T arr[], int l, int mid, int r){
T aux[r-l+];
//T *aux = new T[r-l+1];
for( int i = l ; i <= r; i ++ )
aux[i-l] = arr[i];
// 初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1
int i = l, j = mid+;
for( int k = l ; k <= r; k ++ ){
if( i > mid ){ // 如果左半部分元素已经全部处理完毕
arr[k] = aux[j-l]; j ++;
}
else if( j > r ){ // 如果右半部分元素已经全部处理完毕
arr[k] = aux[i-l]; i ++;
}
else if( aux[i-l] < aux[j-l] ) { // 左半部分所指元素 < 右半部分所指元素
arr[k] = aux[i-l]; i ++;
}
else{ // 左半部分所指元素 >= 右半部分所指元素
arr[k] = aux[j-l]; j ++;
}
}
//delete[] aux;
}
// 使用优化的归并排序算法, 对arr[l...r]的范围进行排序
template<typename T>
void __mergeSort(T arr[], int l, int r){
// 对于小规模数组, 使用插入排序
if( r - l <= ){
insertionSort(arr, l, r);
return;
}
int mid = (l+r)/;
__mergeSort(arr, l, mid);
__mergeSort(arr, mid+, r);
// 对于arr[mid] <= arr[mid+1]的情况,不进行merge
// 对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失
if( arr[mid] > arr[mid+] )
__merge(arr, l, mid, r);
}
template<typename T>
void mergeSort(T arr[], int n){
__mergeSort( arr , , n- );
}
#endif
3.优化时要用的插入排序：
#ifndef INC_06_QUICK_SORT_DEAL_WITH_NEARLY_ORDERED_ARRAY_INSERTIONSORT_H
#define INC_06_QUICK_SORT_DEAL_WITH_NEARLY_ORDERED_ARRAY_INSERTIONSORT_H
#include <iostream>
#include <algorithm>
using namespace std;
template<typename T>
void insertionSort(T arr[], int n){
for( int i = ; i < n ; i ++ ) {
T e = arr[i];
int j;
for (j = i; j > && arr[j-] > e; j--)
arr[j] = arr[j-];
arr[j] = e;
}
return;
}
// 对arr[l...r]范围的数组进行插入排序
template<typename T>
void insertionSort(T arr[], int l, int r){
for( int i = l+ ; i <= r ; i ++ ) {
T e = arr[i];
int j;
for (j = i; j > l && arr[j-] > e; j--)
arr[j] = arr[j-];
arr[j] = e;
}
return;
}
#endif
4.单路快排实现：
#include <iostream>
#include <algorithm>
#include <ctime>
#include "SortTestHelper.h"
#include "MergeSort.h"
#include "InsertionSort.h"
using namespace std;
// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template <typename T>
int _partition(T arr[], int l, int r){
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
swap( arr[l] , arr[rand()%(r-l+)+l] );
T v = arr[l];
int j = l;
for( int i = l + ; i <= r ; i ++ )
if( arr[i] < v ){
j ++;
swap( arr[j] , arr[i] );
}
swap( arr[l] , arr[j]);
return j;
}
// 对arr[l...r]部分进行快速排序
template <typename T>
void _quickSort(T arr[], int l, int r){
// 对于小规模数组, 使用插入排序进行优化
if( r - l <= ){
insertionSort(arr,l,r);
return;
}
int p = _partition(arr, l, r);
_quickSort(arr, l, p- );
_quickSort(arr, p+, r);
}
template <typename T>
void quickSort(T arr[], int n){
srand(time(NULL));
_quickSort(arr, , n-);
}
// 比较Merge Sort和Quick Sort两种排序算法的性能效率
int main() {
int n = ;
// 测试1 一般性测试（随机数）
cout<<"Test for random array, size = "<<n<<", random range [0, "<<n<<"]"<<endl;
int* arr1 = SortTestHelper::generateRandomArray(n,,n);
int* arr2 = SortTestHelper::copyIntArray(arr1,n);
SortTestHelper::testSort("Merge Sort", mergeSort, arr1, n);
SortTestHelper::testSort("Quick Sort", quickSort, arr2, n);
delete[] arr1;
delete[] arr2;
cout<<endl;
// 测试2 测试近乎有序的数组
// 加入了随机选择标定点的步骤后, 我们的快速排序可以轻松处理近乎有序的数组
// 但是对于近乎有序的数组, 其效率比优化后的归并排序要低, 但完全再容忍范围里
int swapTimes = ;
cout<<"Test for nearly ordered array, size = "<<n<<", swap time = "<<swapTimes<<endl;
arr1 = SortTestHelper::generateNearlyOrderedArray(n,swapTimes);
arr2 = SortTestHelper::copyIntArray(arr1, n);
SortTestHelper::testSort("Merge Sort", mergeSort, arr1, n);
SortTestHelper::testSort("Quick Sort", quickSort, arr2, n);
delete[] arr1;
delete[] arr2;
cout<<endl;
// 测试3 测试存在包含大量相同元素的数组
// 但此时, 对于含有大量相同元素的数组, 我们的快速排序算法再次退化成了O(n^2)级别的算法
cout<<"Test for random array, size = "<<n<<", random range [0,10]"<<endl;
arr1 = SortTestHelper::generateRandomArray(n,,);
arr2 = SortTestHelper::copyIntArray(arr1, n);
SortTestHelper::testSort("Merge Sort", mergeSort, arr1, n);
SortTestHelper::testSort("Quick Sort", quickSort, arr2, n);
delete[] arr1;
delete[] arr2;
return ;
}
图解单路快排：
5.单路快排的测试结果：
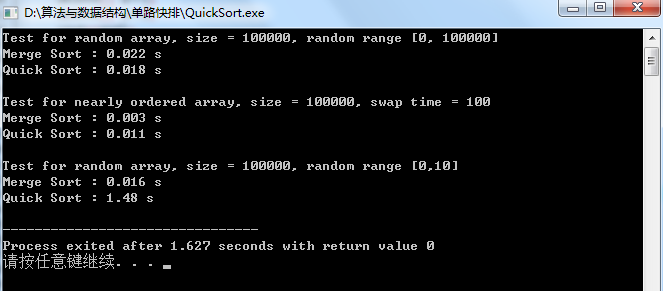
可见单路快排在随机测试和近乎有序的情况下效率是完全可以接受的，但是在存在大量重复的元素中表现不是太好，下面我们进行一步一步的优化：
二，双路快排：
只需改一下主函数：
#include <iostream>
#include <algorithm>
#include <ctime>
#include "SortTestHelper.h"
#include "MergeSort.h"
#include "InsertionSort.h"
using namespace std;
// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template <typename T>
int _partition(T arr[], int l, int r){
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
swap( arr[l] , arr[rand()%(r-l+)+l] );
T v = arr[l];
int j = l;
for( int i = l + ; i <= r ; i ++ )
if( arr[i] < v ){
j ++;
swap( arr[j] , arr[i] );
}
swap( arr[l] , arr[j]);
return j;
}
// 双路快速排序的partition
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template <typename T>
int _partition2(T arr[], int l, int r){
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
swap( arr[l] , arr[rand()%(r-l+)+l] );
T v = arr[l];
// arr[l+1...i) <= v; arr(j...r] >= v
int i = l+, j = r;
while( true ){
// 注意这里的边界, arr[i] < v, 不能是arr[i] <= v
while( i <= r && arr[i] < v )
i ++;
// 注意这里的边界, arr[j] > v, 不能是arr[j] >= v
while( j >= l+ && arr[j] > v )
j --;
if( i > j )
break;
swap( arr[i] , arr[j] );
i ++;
j --;
}
swap( arr[l] , arr[j]);
return j;
}
// 对arr[l...r]部分进行快速排序
template <typename T>
void _quickSort(T arr[], int l, int r){
// 对于小规模数组, 使用插入排序进行优化
if( r - l <= ){
insertionSort(arr,l,r);
return;
}
// 调用双路快速排序的partition
int p = _partition2(arr, l, r);
_quickSort(arr, l, p- );
_quickSort(arr, p+, r);
}
template <typename T>
void quickSort(T arr[], int n){
srand(time(NULL));
_quickSort(arr, , n-);
}
// 比较Merge Sort和双路快速排序两种排序算法的性能效率
int main() {
int n = ;
// 测试1 一般性测试
cout<<"Test for random array, size = "<<n<<", random range [0, "<<n<<"]"<<endl;
int* arr1 = SortTestHelper::generateRandomArray(n,,n);
int* arr2 = SortTestHelper::copyIntArray(arr1,n);
SortTestHelper::testSort("Merge Sort", mergeSort, arr1, n);
SortTestHelper::testSort("Quick Sort", quickSort, arr2, n);
delete[] arr1;
delete[] arr2;
cout<<endl;
// 测试2 测试近乎有序的数组
// 双路快速排序算法也可以轻松处理近乎有序的数组
int swapTimes = ;
cout<<"Test for nearly ordered array, size = "<<n<<", swap time = "<<swapTimes<<endl;
arr1 = SortTestHelper::generateNearlyOrderedArray(n,swapTimes);
arr2 = SortTestHelper::copyIntArray(arr1, n);
SortTestHelper::testSort("Merge Sort", mergeSort, arr1, n);
SortTestHelper::testSort("Quick Sort", quickSort, arr2, n);
delete[] arr1;
delete[] arr2;
cout<<endl;
// 测试3 测试存在包含大量相同元素的数组
// 使用双快速排序后, 我们的快速排序算法可以轻松的处理包含大量元素的数组
cout<<"Test for random array, size = "<<n<<", random range [0,10]"<<endl;
arr1 = SortTestHelper::generateRandomArray(n,,);
arr2 = SortTestHelper::copyIntArray(arr1, n);
SortTestHelper::testSort("Merge Sort", mergeSort, arr1, n);
SortTestHelper::testSort("Quick Sort", quickSort, arr2, n);
delete[] arr1;
delete[] arr2;
return ;
}
图解双路快排：
双路快排测试结果：
可见优化后的双路快排在大量重复元素的数组测试中速度提升了近乎200倍，接下来让我们在来看看最棒的三路快排：
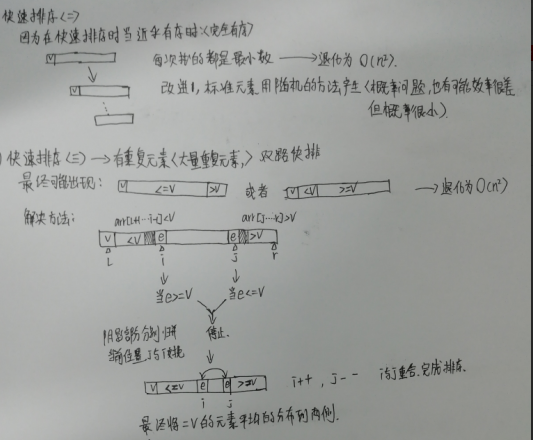
三，三路快排：
1.我们将刚才的双路快排写到一个头文件中以便等下测试：
#ifndef INC_07_QUICK_SORT_THREE_WAYS_QUICKSORT_H
#define INC_07_QUICK_SORT_THREE_WAYS_QUICKSORT_H
#include <iostream>
#include <ctime>
#include <algorithm>
#include "InsertionSort.h"
using namespace std;
// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template <typename T>
int _partition(T arr[], int l, int r){
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
swap( arr[l] , arr[rand()%(r-l+1)+l] );
T v = arr[l];
int j = l;
for( int i = l + 1 ; i <= r ; i ++ )
if( arr[i] < v ){
j ++;
swap( arr[j] , arr[i] );
}
swap( arr[l] , arr[j]);
return j;
}
// 双路快速排序的partition
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template <typename T>
int _partition2(T arr[], int l, int r){
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
swap( arr[l] , arr[rand()%(r-l+1)+l] );
T v = arr[l];
int i = l+1, j = r;
while( true ){
// 注意这里的边界, arr[i] < v, 不能是arr[i] <= v
while( i <= r && arr[i] < v )
i ++;
// 注意这里的边界, arr[j] > v, 不能是arr[j] >= v
while( j >= l+1 && arr[j] > v )
j --;
if( i > j )
break;
swap( arr[i] , arr[j] );
i ++;
j --;
}
swap( arr[l] , arr[j]);
return j;
}
// 对arr[l...r]部分进行快速排序
template <typename T>
void _quickSort(T arr[], int l, int r){
// 对于小规模数组, 使用插入排序进行优化
if( r - l <= 15 ){
insertionSort(arr,l,r);
return;
}
// 调用双路快速排序的partition
int p = _partition2(arr, l, r);
_quickSort(arr, l, p-1 );
_quickSort(arr, p+1, r);
}
template <typename T>
void quickSort(T arr[], int n){
srand(time(NULL));
_quickSort(arr, 0, n-1);
}
#endif
2.三路快排实现：
#include <iostream>
#include <algorithm>
#include <ctime>
#include "SortTestHelper.h"
#include "MergeSort.h"
#include "InsertionSort.h"
#include "QuickSort.h"
using namespace std;
// 递归的三路快速排序算法
template <typename T>
void __quickSort3Ways(T arr[], int l, int r){
// 对于小规模数组, 使用插入排序进行优化
if( r - l <= ){
insertionSort(arr,l,r);
return;
}
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
swap( arr[l], arr[rand()%(r-l+)+l ] );
T v = arr[l];
int lt = l; // arr[l+1...lt] < v
int gt = r + ; // arr[gt...r] > v
int i = l+; // arr[lt+1...i) == v
while( i < gt ){
if( arr[i] < v ){
swap( arr[i], arr[lt+]);
i ++;
lt ++;
}
else if( arr[i] > v ){
swap( arr[i], arr[gt-]);
gt --;
}
else{ // arr[i] == v
i ++;
}
}
swap( arr[l] , arr[lt] );
__quickSort3Ways(arr, l, lt-);
__quickSort3Ways(arr, gt, r);
}
template <typename T>
void quickSort3Ways(T arr[], int n){
srand(time(NULL));
__quickSort3Ways( arr, , n-);
}
int main() {
int n = ;
// 测试1 一般性测试
cout<<"一般随机测试："<<endl;
cout<<"Test for random array, size = "<<n<<", random range [0, "<<n<<"]"<<endl;
int* arr1 = SortTestHelper::generateRandomArray(n,,n);
int* arr2 = SortTestHelper::copyIntArray(arr1,n);
int* arr3 = SortTestHelper::copyIntArray(arr1,n);
SortTestHelper::testSort("Merge Sort", mergeSort, arr1, n);
SortTestHelper::testSort("Quick Sort", quickSort, arr2, n);
SortTestHelper::testSort("Quick Sort 3 Ways", quickSort3Ways, arr3, n);
delete[] arr1;
delete[] arr2;
delete[] arr3;
cout<<endl;
// 测试2 测试近乎有序的数组
cout<<"测试近乎有序的数组"<<endl;
int swapTimes = ;
cout<<"Test for nearly ordered array, size = "<<n<<", swap time = "<<swapTimes<<endl;
arr1 = SortTestHelper::generateNearlyOrderedArray(n,swapTimes);
arr2 = SortTestHelper::copyIntArray(arr1, n);
arr3 = SortTestHelper::copyIntArray(arr1, n);
SortTestHelper::testSort("Merge Sort", mergeSort, arr1, n);
SortTestHelper::testSort("Quick Sort", quickSort, arr2, n);
SortTestHelper::testSort("Quick Sort 3 Ways", quickSort3Ways, arr3, n);
delete[] arr1;
delete[] arr2;
delete[] arr3;
cout<<endl;
// 测试3 测试存在包含大量相同元素的数组
cout<<"测试存在包含大量相同元素的数组"<<endl;
cout<<"Test for random array, size = "<<n<<", random range [0,10]"<<endl;
arr1 = SortTestHelper::generateRandomArray(n,,);
arr2 = SortTestHelper::copyIntArray(arr1, n);
arr3 = SortTestHelper::copyIntArray(arr1, n);
SortTestHelper::testSort("Merge Sort", mergeSort, arr1, n);
SortTestHelper::testSort("Quick Sort", quickSort, arr2, n);
SortTestHelper::testSort("Quick Sort 3 Ways", quickSort3Ways, arr3, n);
delete[] arr1;
delete[] arr2;
delete[] arr3;
return ;
}
图解三路快排：
三路快排运行结果：
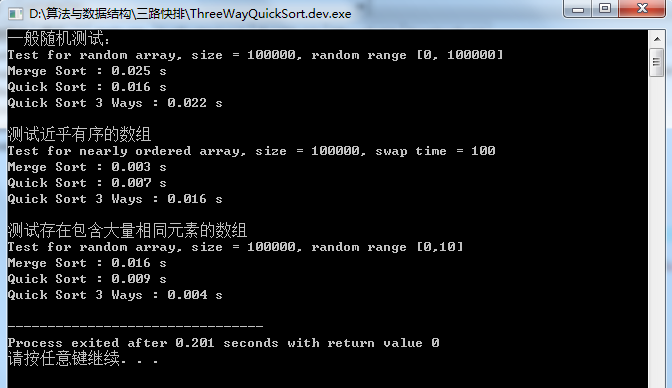
可见性能又进一步提升了：
比较Merge Sort和双路快速排序和三路快排三种排序算法的性能效率
对于包含有大量重复数据的数组, 三路快排有巨大的优势
对于一般性的随机数组和近乎有序的数组, 三路快排的效率虽然不是最优的, 但是在可以接受的范围里
因此, 在一些语言中, 三路快排是默认的语言库函数中使用的排序算法。比如Java:)
O(n*logn)级别的算法之二（快速排序）的三种实现方法详解及其与归并排序的对比的更多相关文章
- “全栈2019”Java多线程第十二章：后台线程setDaemon()方法详解
难度 初级 学习时间 10分钟 适合人群 零基础 开发语言 Java 开发环境 JDK v11 IntelliJ IDEA v2018.3 文章原文链接 "全栈2019"Java多 ...
- （二）线程Thread中的方法详解
1.start() start()方法的作用讲得直白点就是通知"线程规划器",此线程可以运行了,正在等待CPU调用线程对象得run()方法,产生一个异步执行的效果.通过start( ...
- Java构造和解析Json数据的两种方法详解二
在www.json.org上公布了很多JAVA下的json构造和解析工具,其中org.json和json-lib比较简单,两者使用上差不多但还是有些区别.下面接着介绍用org.json构造和解析Jso ...
- 《Android群英传》读书笔记 (5) 第十一章 搭建云端服务器 + 第十二章 Android 5.X新特性详解 + 第十三章 Android实例提高
第十一章 搭建云端服务器 该章主要介绍了移动后端服务的概念以及Bmob的使用,比较简单,所以略过不总结. 第十三章 Android实例提高 该章主要介绍了拼图游戏和2048的小项目实例,主要是代码,所 ...
- Android群英传笔记——第十二章：Android5.X 新特性详解，Material Design UI的新体验
Android群英传笔记--第十二章:Android5.X 新特性详解,Material Design UI的新体验 第十一章为什么不写,因为我很早之前就已经写过了,有需要的可以去看 Android高 ...
- qml学习笔记(二)：可视化元素基类Item详解（上半场anchors等等）
原博主博客地址:http://blog.csdn.net/qq21497936本文章博客地址:http://blog.csdn.net/qq21497936/article/details/78516 ...
- “全栈2019”Java第三十一章：二维数组和多维数组详解
难度 初级 学习时间 10分钟 适合人群 零基础 开发语言 Java 开发环境 JDK v11 IntelliJ IDEA v2018.3 文章原文链接 "全栈2019"Java第 ...
- Java构造和解析Json数据的两种方法详解二——org.json
转自:http://www.cnblogs.com/lanxuezaipiao/archive/2013/05/24/3096437.html 在www.json.org上公布了很多JAVA下的jso ...
- java多线程并发（二）--线程的生命周期及方法详解
上篇随笔介绍了线程的相关基础知识以及新启线程的几种方法,本片将继续介绍线程的生命周期及方法详解. 一.线程的生命周期 在Thread代码中,线程的状态被分为6种 public enum State { ...
随机推荐
- FCC（ES6写法） Inventory Update
依照一个存着新进货物的二维数组,更新存着现有库存(在 arr1 中)的二维数组. 如果货物已存在则更新数量 . 如果没有对应货物则把其加入到数组中,更新最新的数量. 返回当前的库存数组,且按货物名称的 ...
- C++的结构体指针传参
typedef struct node{int n;node *left;}*tnode; 传参的时候注意用** void init(node **nn);int main(){tnode nna;i ...
- 【XSS】利用 onload 事件监控流量劫持
说到跨站资源监控,首先会联想到『Content Security Policy』.既然 CSP 好用,我们何必自己再搞一套呢.那就先来吐槽下 CSP 的缺陷. 目前的 CSP 日志不详细 用过 CSP ...
- 1.7 All components require plug-in?
In Android, Activity, Service, ContentProvider, and BroadcastReceiver are called as four major compo ...
- 微信小程序wx.request请求用POST后台得不到传递数据
微信小程序的wx.request请求,method设为POST并向后台传递数据,但从后台返回的信息来看后台并没有获得传递的数据 wx.request({ url: 'url' ...
- emWin监护仪界面设计，含uCOS-III和FreeRTOS两个版本
第5期:监护仪界面设计 配套例子:V6-908_STemWin提高篇实验_监护仪界面设计(uCOS-III)V6-909_STemWin提高篇实验_监护仪界面设计(FreeRTOS) 例程下载地址:h ...
- 打个响指Selenium自动化开启
最近斗哥在朋友的影响下,接触了自动化测试工具中的一个项目:appium自动化测试脚本. appium类库封装了标准Selenium客户端类库,为用户提供所有常见的JSON格式selenium命令以及额 ...
- Javascript高级编程学习笔记（88）—— Canvas(5)绘制文本
绘制文本 同样的,canvas也为绘制文本提供了相应的方法. 2D上下文提供的文本绘制方法主要有两个: fillText() strokeText() 这两个方法都接受四个参数 要绘制的文本字符串 绘 ...
- [Swift]LeetCode913.猫与老鼠 | Cat and Mouse
A game on an undirected graph is played by two players, Mouse and Cat, who alternate turns. The grap ...
- Linux 安装 Kafka
1. 下载安装包 官网下载地址:http://kafka.apache.org/downloads 选择一个版本下载,然后解压安装包. 2. 基本使用 2.1 启动kafka bin/zookeepe ...