【机器学习】--线性回归中L1正则和L2正则

一、前述

L1正则，L2正则的出现原因是为了推广模型的泛化能力。相当于一个惩罚系数。

二、原理

L1正则：Lasso Regression

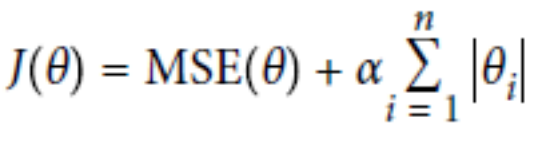
L2正则：Ridge Regression

总结：

经验值 MSE前系数为1 ，L1 , L2正则前面系数一般为0.4~0.5 更看重的是准确性。

L2正则会整体的把w变小。

L1正则会倾向于使得w要么取1，要么取0 ，稀疏矩阵 ，可以达到降维的角度。

ElasticNet函数（把L1正则和L2正则联合一起）：

总结：

1.默认情况下选用L2正则。

2.如若认为少数特征有用，可以用L1正则。

3.如若认为少数特征有用，但特征数大于样本数，则选择ElasticNet函数。

 代码一：L1正则

# L1正则
import numpy as np
from sklearn.linear_model import Lasso
from sklearn.linear_model import SGDRegressor
 
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
 
lasso_reg = Lasso(alpha=0.15)
lasso_reg.fit(X, y)
print(lasso_reg.predict(1.5))
 
sgd_reg = SGDRegressor(penalty='l1')
sgd_reg.fit(X, y.ravel())
print(sgd_reg.predict(1.5))

代码二：L2正则

# L2正则
import numpy as np
from sklearn.linear_model import Ridge
from sklearn.linear_model import SGDRegressor
 
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
 
#两种方式第一种岭回归
ridge_reg = Ridge(alpha=1, solver='auto')
ridge_reg.fit(X, y)
print(ridge_reg.predict(1.5))#预测1.5的值
#第二种 使用随机梯度下降中L2正则
sgd_reg = SGDRegressor(penalty='l2')
sgd_reg.fit(X, y.ravel())
print(sgd_reg.predict(1.5))

代码三：Elastic_Net函数

# elastic_net函数
import numpy as np
from sklearn.linear_model import ElasticNet
from sklearn.linear_model import SGDRegressor
 
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
#两种方式实现Elastic_net
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
print(elastic_net.predict(1.5))
 
sgd_reg = SGDRegressor(penalty='elasticnet')
sgd_reg.fit(X, y.ravel())
print(sgd_reg.predict(1.5))