从零开始一起学习SLAM | 点云到网格的进化

点击公众号“计算机视觉life”关注，置顶星标更快接收消息！
本文编程练习框架及数据获取方法见文末获取方式
菜单栏点击“知识星球”查看「从零开始学习SLAM」一起学习交流

小白：师兄，师兄，你在《从零开始一起学习SLAM | 给点云加个滤网》、《从零开始一起学习SLAM | 点云平滑法线估计》中都提到了点云网格化，这个听起来高大上，不过到底是什么意思呢？

师兄：别急，是这样的：你看我们之前处理的都是一个个点，不管是滤波还是平滑，我们都是对一个个离散的空间点进行的处理，虽然你远看能看出物体的轮廓，但是拉近了看是一个个分散的空间点，是吧？

小白：是啊，这样不算是3D模型吧

师兄：嗯，这样的结果分辨率比较低，也没办法进行三维打印，点云网格化就是用点云生成网格，最后得到的是一个连续（相对于前面的离散点）的表面。如果再加上纹理贴图，就能得到和真实物体一样的三维模型了

什么是网格？

小白：师兄，你说了很多次网格，其实我还不知道网格到底是啥？

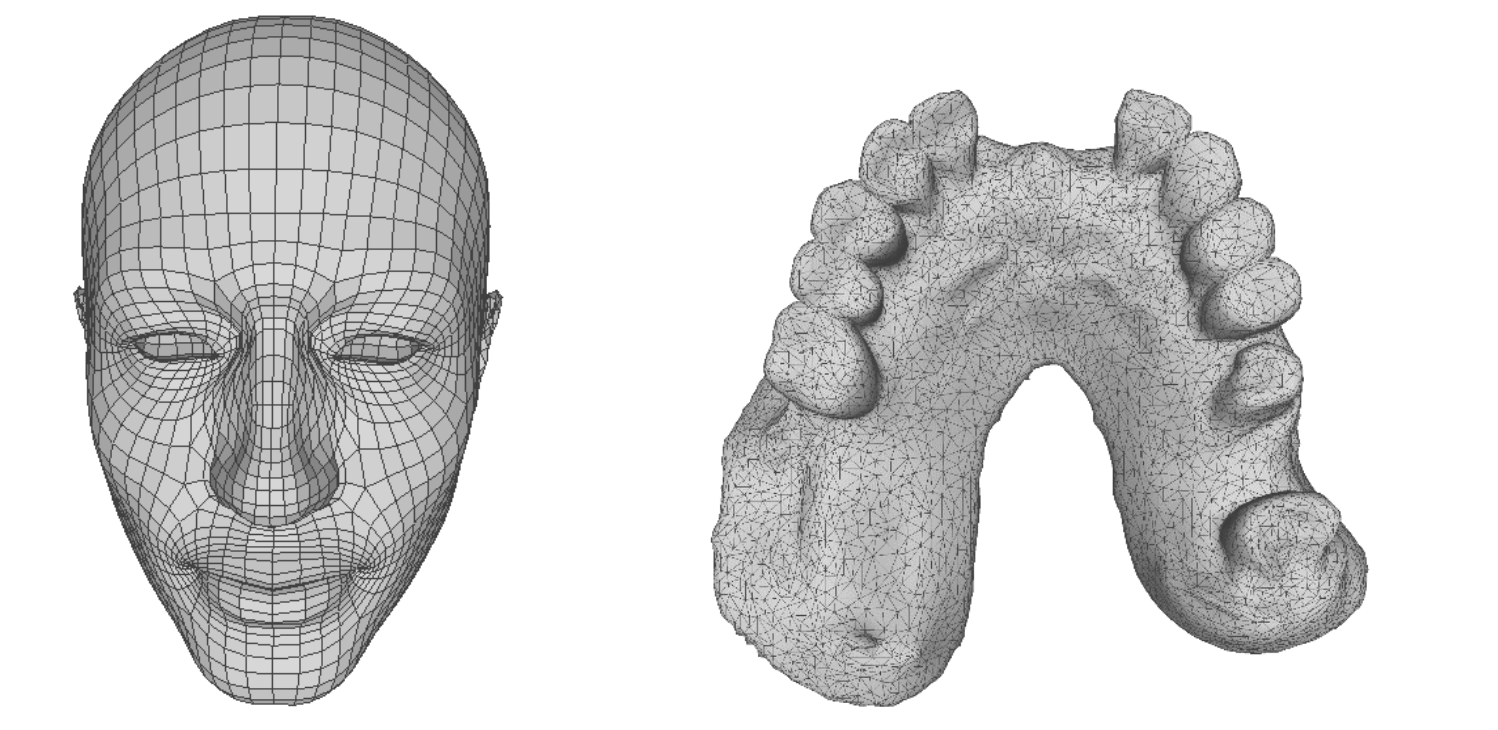
师兄：哦，忘记说这个最基本的概念了。网格主要用于计算机图形学中，有三角、四角网格等很多种。下面左图就是四角网格，右图是三角网格

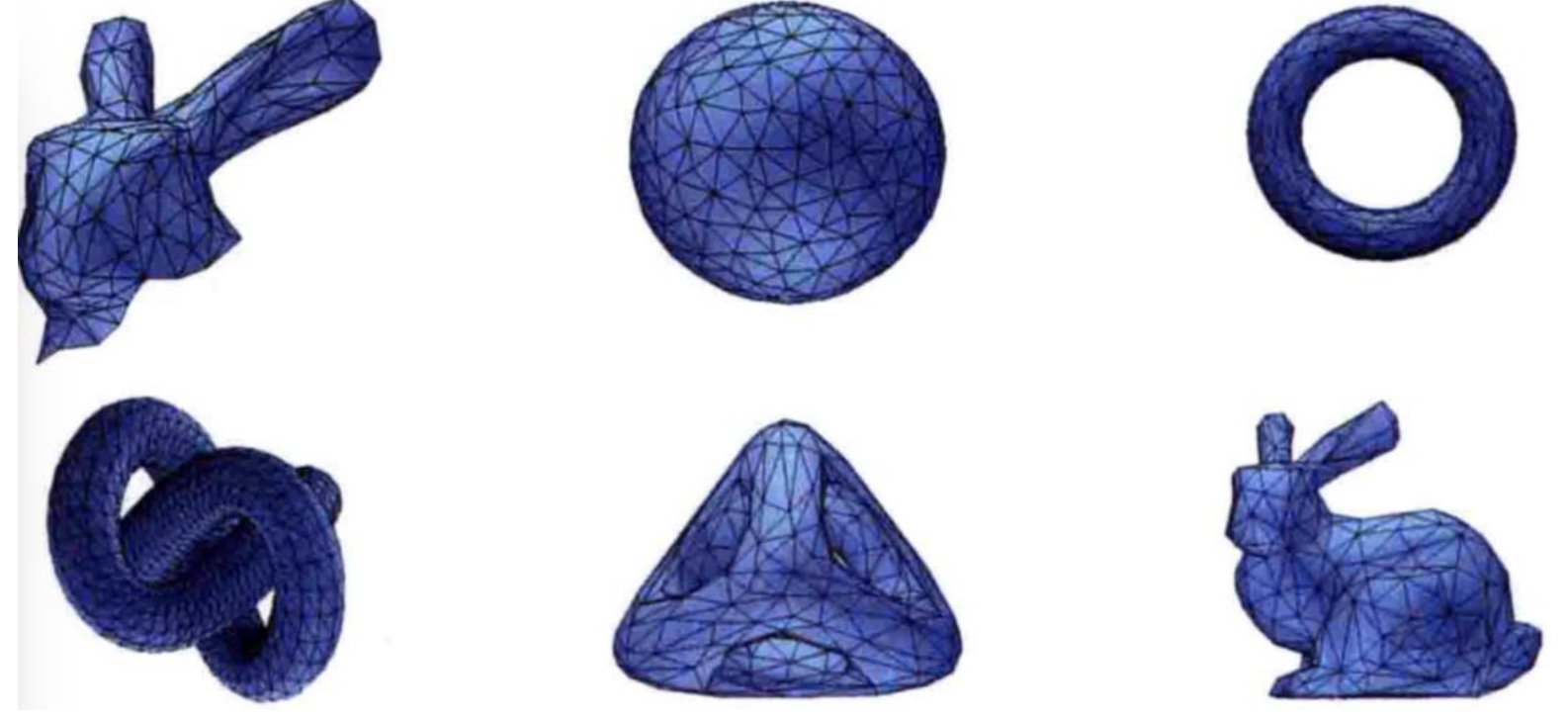
不过，计算机图形学中的网格处理绝大部分都是基于三角网格的，三角网格在图形学和三维建模中使用的非常广泛，用来模拟复杂物体的表面，如建筑、车辆、动物等，你看下图中的兔子、球等模型都是基于三角网格的

小白：仔细看了下还真是，为啥一般用三角网格啊？是因为三角形的稳定性吗？（滑稽）

师兄：还真是一个原因。三角形表示网格也叫三角剖分。它有如下几个优点：

1、正如你所说的，稳定性强。

2、三角网格比较简单（主要原因），实际上三角网格是最简单的网格类型之一，可以非常方便并且快速生成，在非结构化网格中最常见。而且相对于一般多边形网格，许多操作对三角网格更容易。

3、有助于恢复模型的表面细节。

小白：原来如此。三角网格在空间中如何表示呢？

师兄：实际应用中出现的三角网格，每个三角形都和其他三角形共享边。所以三角网格需要存储三类信息：

• 顶点。每个三角形都有三个顶点，各顶点都有可能和其他三角形共享。
• 边。连接两个顶点的边，每个三角形有三条边。
• 面。每个三角形对应一个面，我们可以用顶点或边列表表示面。

网格生成算法有什么要求？

小白：那这个点云网格化一般怎么做呢？

师兄：点云网格化一般输入就是点云啦，输出就是三维网格啦，不过输入的点云一般面临几个问题，我们前面也提到过：

1、点云噪声。 每个点云都会带有噪声，噪声有可能和物体表面光学性质、物体深度、传感器性能等都有关系。

2、点云匹配误差。三维重建中需要将不同帧得到的点云估计其在世界坐标系下的位姿，会引入一定的位置误差。

3、点云分布。分布的不均匀性体现在两个方面。一个是每个点云在不同的方向上分布是不均匀的另一个是不同的点云匹配后，不同位置的点云密度是不一样的。

4、缺失数据。 扫描中如果碰到不易成像的部位（比如不可见、反光等等），那么这部分的数据是缺失的，点云是不完整的。

小白：点云有这么多问题，网格化算法肯定要求比较高了？

师兄：是的，想要生成漂亮的网格，除了网格密度和精度外，我们还希望网格生成算法有如下的能力：

1、对点云噪声有一定的冗余度。

2、能够重建出曲率变化比较大的曲面。

3、能够处理大数据量，算法时间和空间复杂度不会太高。

4、重建出的网格中包含尽可能少的异常三角片，比如三角片交错在一起、表面法向量不连续或不一致、同一个位置附近出现多层三角片等。

小白：感觉要求挺高的，那我们一般用什么算法呢？

师兄：目前点云进行网格生成一般分为两大类方法：

1、 插值法。顾名思义，也就是重建的曲面都是通过原始的数据点得到的

2、逼近法。用分片线性曲面或其他曲面来逼近原始数据点，得到的重建曲面是原始点集的一个逼近。

点云贪心三角化原理

师兄：我们主要介绍一种比较简单的贪心三角化法（对应的类名：pcl::GreedyProjectionTriangulation），也就是使用贪心投影三角化算法对有向点云进行三角化。

小白：为啥介绍这个，有啥特点？

师兄：该算法的优点是可以用来处理来自一个或者多个设备扫描到得到、并且有多个连接处的散乱点云。但是也是有很大的局限性，它更适用于采样点云来自表面连续光滑的曲面，并且点云的密度变化比较均匀的情况

小白：这样啊，难怪之前师兄要讲点云滤波和平滑呢，原来都是铺垫啊

师兄：哈哈，是的。

小白：那这个贪心三角化法到底是什么原理呢？

师兄：贪心投影三角化的大致流程是这样的：

（1）先将点云通过法线投影到某一二维坐标平面内

（2）然后对投影得到的点云做平面内的三角化，从而得到各点的拓扑连接关系。平面三角化的过程中用到了基于Delaunay三角剖分 的空间区域增长算法

（3）最后根据平面内投影点的拓扑连接关系确定各原始三维点间的拓扑连接，所得三角网格即为重建得到的曲面模型

Delaunay 三角剖分简介

小白：师兄，这个Delaunay是啥？

师兄：先说说点集的三角剖分（Triangulation）吧，对数值分析以及图形学来说，三角剖分都是极为重要的一项预处理技术。而Delaunay 三角剖分是一种常用的三角剖分的方法，这个方法比较常见，关于点集的很多种几何图都和Delaunay三角剖分相关，如Voronoi图，当然这些很复杂了。我们这里只是简单介绍一下Delaunay 三角剖分，不然估计你要头大了。

小白：师兄，你一连说了几个我从来没听过的术语，我已经头大了。。

师兄：哈哈，那打住，只简单提一下Delaunay 三角剖分。你看下面这个图，左侧就是不满足Delaunay 三角剖分，右侧是Delaunay 三角剖分的结果。

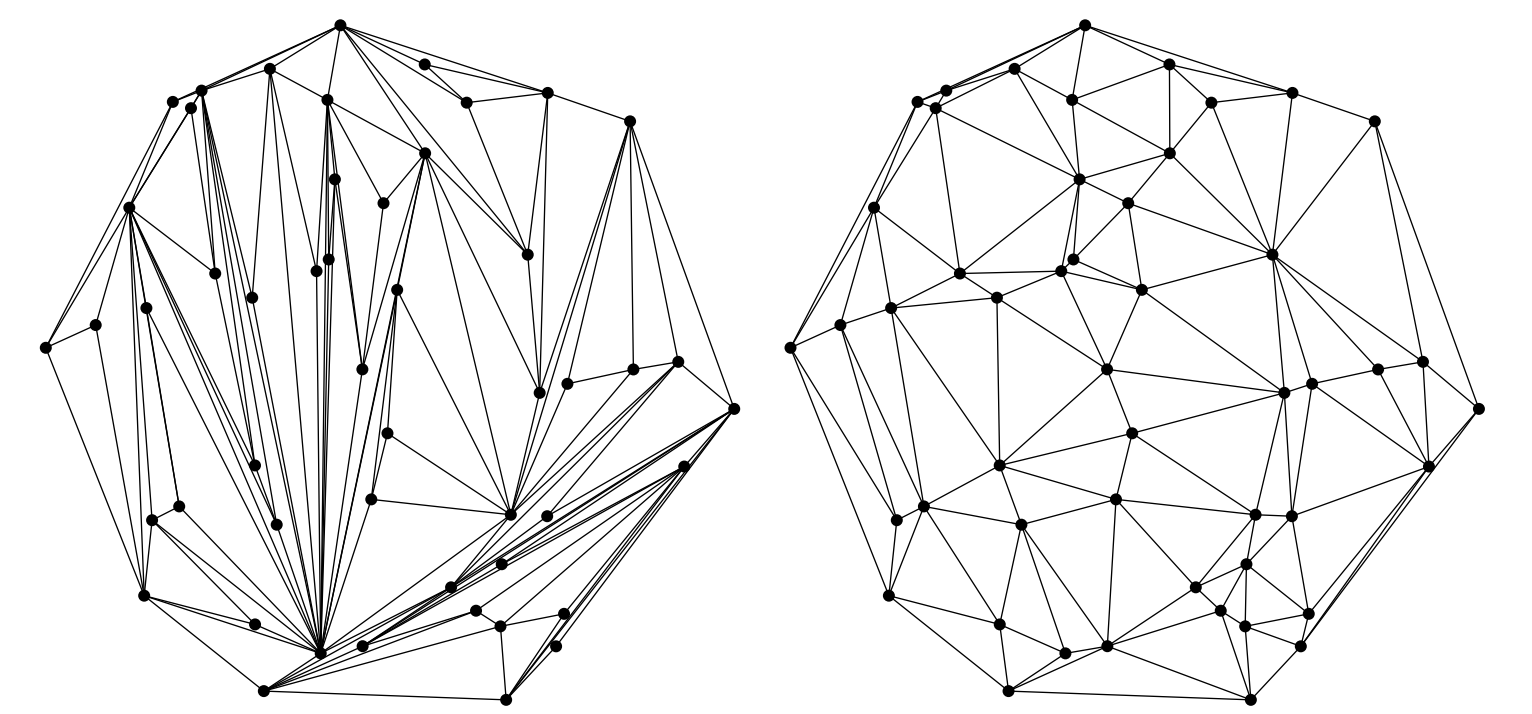
小白：看起来右边的图好像很规则啊

师兄：的确，Delaunay 三角剖分的有两个优点：

1.最大化最小角，“最接近于规则化的“的三角网。

2.唯一性（任意四点不能共圆）。

我们来看一下它的定义，有点拗口：点集