算法练习：最小生成树 (Minimum Spanning Tree)

（注：此贴是为了回答同事提出的一个问题而匆匆写就，算法代码只求得出答案为目的，效率方面还有很大的改进空间）

最小生成树是指对于给定的带权无向图，需要生成一个总权重最小的连通图。
其问题描述及算法可以详见：https://en.wikipedia.org/wiki/Minimum_spanning_tree
以下我选用其中一个简单的算法描述，编写 Python 代码尝试解决此问题。

下面是同事提出的问题的原图：

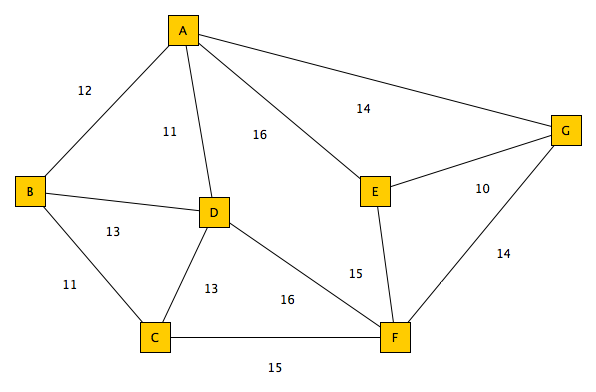
程序：

 # coding: utf-8

 from sets import Set

 def edge_name(v1, v2):
     if v1 < v2:
         return v1 + v2
     return v2 + v1

 # Prim algorithm
 def mst(vectors, costs, vectors_in_g, edges_in_g):
     if len(vectors) == len(vectors_in_g):
         return (vectors_in_g, edges_in_g)

     min_cost = max(costs.values()) + 1
     remaining_vectors = vectors.difference(vectors_in_g)
     next_vector = ''
     next_edge = ''

     for x in vectors_in_g:
         for y in remaining_vectors:
             ename = edge_name(x, y)
             if ename not in costs:
                 continue
             cost = costs[ename]
             if cost < min_cost:
                 next_vector = y
                 next_edge = ename
                 min_cost = cost

     if next_vector <> '' and next_edge <> '':
         new_vectors_in_g = vectors_in_g.copy()
         new_edges_in_g = edges_in_g[:]
         new_vectors_in_g.add(next_vector)
         new_edges_in_g.append(next_edge)

         return mst(vectors, costs, new_vectors_in_g, new_edges_in_g)
     else:
         raise Exception("The MST can not be found.")

 my_vectors = Set(['a', 'b', 'c', 'd', 'e', 'f', 'g'])
 my_costs = {
     'ab': 12,
     'ad': 11,
     'ae': 16,
     'ag': 14,
     'bc': 11,
     'bd': 13,
     'cd': 13,
     'cf': 15,
     'df': 16,
     'ef': 15,
     'eg': 10,
     'fg': 14
 }

 vs, es = mst(my_vectors, my_costs, Set(list(my_vectors)[0]), [])

 print vs
 print es

 total_cost = 0
 for e in es:
     total_cost += my_costs[e]

 print total_cost

程序输出如下：

Set(['a', 'c', 'b', 'e', 'd', 'g', 'f'])
['ad', 'ab', 'bc', 'ag', 'eg', 'fg']
72

从输出结果可知最优解的总权重72. 图示如下：