dp算法之有代价的最短路径

题目：有代价的最短路径

题目介绍：如下图所示，现在平面上有N个点，此时N=7，每个点可能和其他点相连，相连的线有一定权值，求出从0点到N-1点的消耗权值的最小值。

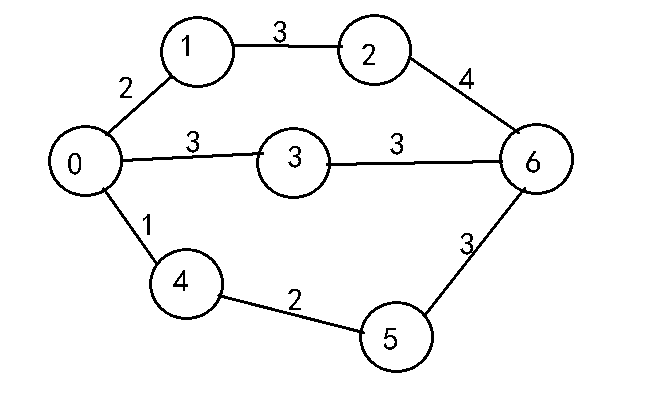
分析：用动态规划的思路来解决，每一点与其他点的消耗权值的最小值都储存在一个二维数组中，下一个点消耗的最小值可以根据前一个点来得出。如果两个点不相连，可以认为这两点的权值为无穷大。设一个二维数组初始化为无穷，再导入权值初始值，再用状态方程得出最小值储存在数组中。

状态方程：l[k][j] = min(l[k][j], l[k][i] + l[i][j])

我们可以得出0到N-1的最短路径表格：

距离	0	1	2	3	4	5	6
0	0	2	5	3	1	3	6

代码：

 #include <iostream>
 using namespace std;
 int min(int a, int b);
 int main()
 {
     int X = ;
     int N = ;
     int i, j, k;
     int **l = new int *[N];
     for (i = ; i<N; i++)
     {
         l[i] = new int[N];
     }
     for (i = ; i < N; i++)
     {
         for (j = ; j < N; j++)
         {
             l[i][j] = X;
         }
     }
     l[][] = l[][] = ;
     l[][] = l[][] = ;
     l[][] = l[][] = ;
     l[][] = l[][] = ;
     l[][] = l[][] = ;
     l[][] = l[][] = ;
     l[][] = l[][] = ;
     l[][] = l[][] = ;
     for (k = ; k < N; k++)
     {
         for (j = ; j < N; j++)
         {
             for (i = ; i < N; i++)
             {
                 l[k][j] = min(l[k][j], l[k][i] + l[i][j]);
             }
         }
     }
     for (i = ; i < N; i++)
     {
         cout << l[][i] << endl;
     }
 }
 int min(int a, int b)
 {
     if (a > b)
     {
         return b;
     }
     else { return a; }
 }

结果：