AVL树/线索二叉树

此文转载：

http://www.cnblogs.com/skywang12345/p/3577360.html

AVL树是一棵特殊的高度平衡的二叉树，每个节点的两棵子树高度最大差为1。所以在每次的删除或者是插入的过程之后都要判断此时是否是一颗AVL树，AVL树不平衡的调整最关键，大概分为四种不同的不平衡的状态。处理四种不平衡状态四个调整函数（LL,RR,LR,Rl）即可；

(1) LL：LeftLeft，也称为"左左"。插入或删除一个节点后，根节点的左子树的左子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。

例如，在上面LL情况中，由于"根节点(8)的左子树(4)的左子树(2)还有非空子节点"，而"根节点(8)的右子树(12)没有子节点"；导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。

(2) LR：LeftRight，也称为"左右"。插入或删除一个节点后，根节点的左子树的右子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。

例如，在上面LR情况中，由于"根节点(8)的左子树(4)的左子树(6)还有非空子节点"，而"根节点(8)的右子树(12)没有子节点"；导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。

(3) RL：RightLeft，称为"右左"。插入或删除一个节点后，根节点的右子树的左子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。

例如，在上面RL情况中，由于"根节点(8)的右子树(12)的左子树(10)还有非空子节点"，而"根节点(8)的左子树(4)没有子节点"；导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。

(4) RR：RightRight，称为"右右"。插入或删除一个节点后，根节点的右子树的右子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。

例如，在上面RR情况中，由于"根节点(8)的右子树(12)的右子树(14)还有非空子节点"，而"根节点(8)的左子树(4)没有子节点"；导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。

LL旋转：

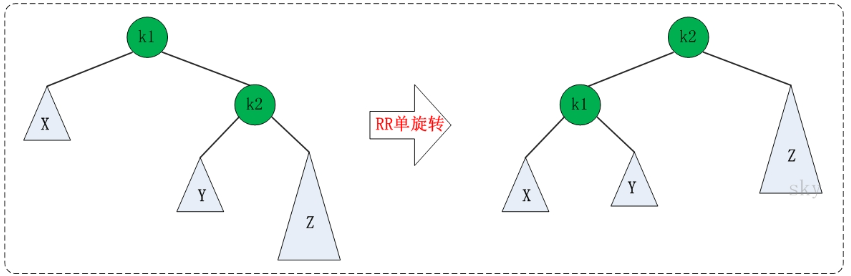
RR旋转：

LR旋转：

RL旋转：

因为博客园中我还不知道如何转载原文，所以只能以这种方式；

第八次作业：

下面是我自己根据原文代码做题写的C语言的代码（没有全A，不知为何）

2、题目链接（多次删除操作多次寻找树中的最大最小值）：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<malloc.h>
using namespace std;
int n;
int nodes[100005];
int dep[100005];
int depth = 0;
typedef struct AVL_Node
{
	int data;
	int height;
	AVL_Node* left;
	AVL_Node* right;
}Node, *AVLTree;

int MAX(int a, int b)
{
	return a < b ? b : a;
}

int Height(AVLTree tree)						//返回该节点树的高度；
{
	return tree == NULL ? 0 : tree->height;
}

Node* create_node(int data, Node* left, Node* right)
{
	Node* p;
	if ((p = (Node*)malloc(sizeof(Node))) == NULL)
		return NULL;
	p->data = data;
	p->height = 0;
	p->left = left;
	p->right = right;
	return p;
}

Node* L_L(AVLTree tree)
{
	AVLTree tmp;
	tmp = tree->left;
	tree->left = tmp->right;
	tmp->right = tree;
	tree->height = MAX(Height(tree->left), Height(tree->right)) + 1;
	tmp->height = MAX(Height(tmp->left), tree->height) + 1;
	return tmp;
}

Node* R_R(AVLTree tree)
{
	AVLTree tmp;
	tmp = tree->right;
	tree->right = tmp->left;
	tmp->left = tree;
	tree->height = MAX(Height(tree->left), Height(tree->right)) + 1;
	tmp->height = MAX(Height(tmp->right), tree->height) + 1;
	return tmp;
}

Node* L_R(AVLTree tree)
{
	tree->left = R_R(tree->left);
	return L_L(tree);
}

Node* R_L(AVLTree tree)
{
	tree->right = L_L(tree->right);
	return R_R(tree);
}
Node* maximum(Node* tree)
{
	if (tree == NULL)return NULL;
	while(tree->right!=NULL)
	{
		tree = tree->right;
	}
	return tree;
}
Node* minimun(Node* tree)
{
	if (tree == NULL)return NULL;
	while(tree->left!=NULL)
	{
		tree = tree->left;
	}
	return tree;
}

Node* insert(AVLTree tree, int data)
{
	if (tree == NULL)
	{
		tree = create_node(data, NULL, NULL);
		if (tree == NULL)
			return NULL;
	}
	else if (data < tree->data)			//根据AVL树的性质应该插入到左子树中
	{
		tree->left = insert(tree->left, data);
		if (Height(tree->left) - Height(tree->right) == 2)		//插入后树如果不平衡，则应进行调节；
		{
			if (data < tree->left->data)
				tree = L_L(tree);
			else
				tree = L_R(tree);
		}
	}
	else if (data > tree->data)
	{
		tree->right = insert(tree->right, data);
		if (Height(tree->right) - Height(tree->left) == 2)
		{
			if (data < tree->right->data)
				tree = R_L(tree);
			else
				tree = R_R(tree);
		}
	}
	tree->height = MAX(Height(tree->left), Height(tree->right)) + 1;
	return tree;
}

Node* Delete(AVLTree tree,Node* dele)
{
	if (tree == NULL || dele == NULL)return NULL;		//根为空或者没有要删除的节点，直接返回NULL;
	if (dele->data < tree->data)						//删除节点在左子树中；
	{
		tree->left = Delete(tree->left, dele);
		if (Height(tree->right) - Height(tree->left) == 2)//失去平衡之后要重新调整；
		{
			Node* tmp = tree->right;
			if (Height(tmp->left) > Height(tmp->right))
				tree = R_L(tree);
			else
				tree = R_R(tree);
		}
	}
	else if (dele->data > tree->data)					//删除节点在右子树中；
	{
		tree->right = Delete(tree->right, dele);
		if (Height(tree->left) - Height(tree->right) == 2)//失去平衡之后要重新调整；
		{
			Node* tmp = tree->left;
			if (Height(tmp->right) > Height(tmp->left))
				tree = L_R(tree);
			else
				tree = L_L(tree);
		}
	}
	else
	{
		if ((tree->left != NULL) && (tree->right != NULL))
		{
			if (Height(tree->left) > Height(tree->right))
			{
				// 如果tree的左子树比右子树高；
				// 则(01)找出tree的左子树中的最大节点
				//   (02)将该最大节点的值赋值给tree。
				//   (03)删除该最大节点。
				// 这类似于用"tree的左子树中最大节点"做"tree"的替身；
				// 采用这种方式的好处是：删除"tree的左子树中最大节点"之后，AVL树仍然是平衡的。
				Node* max = maximum(tree->left);
				tree->data = max->data;
				tree->left = Delete(tree->left, max);
			}
			else
			{
				// 如果tree的左子树不比右子树高(即它们相等，或右子树比左子树高1)
				// 则(01)找出tree的右子树中的最小节点
				//   (02)将该最小节点的值赋值给tree。
				//   (03)删除该最小节点。
				// 这类似于用"tree的右子树中最小节点"做"tree"的替身；
				// 采用这种方式的好处是：删除"tree的右子树中最小节点"之后，AVL树仍然是平衡的。
				Node* min = minimun(tree->right);
				tree->data = min->data;
				tree->right = Delete(tree->right, min);
			}
		}
		else
		{
			Node* tmp = tree;
			tree = (tree->left != NULL) ? tree->left : tree->right;
			free(tmp);
		}
	}
	return tree;
}

Node* mininode(AVLTree tree,AVLTree tmproot)			//寻找最小键值的节点；
{
	int depth = 1;
	if (tree == NULL)return NULL;
	while (tree->left != NULL)
	{
		tree = tree->left; depth++;
	}
	cout << tree->data << " " << depth << endl;
	return Delete(tmproot, tree);
}

Node* maxnode(AVLTree tree,AVLTree tmproot)				//寻找最大键值的节点；
{
	int depth = 1;
	if (tree == NULL)return NULL;
	while (tree->right != NULL)
	{
		tree = tree->right; depth++;
	}
	cout << tree->data << " " << depth << endl;
	return Delete(tmproot, tree);
}

int main()
{
	int i, tmp1, tmp2;
	AVLTree root = NULL;
	cin >> n;
	for (i = 1; i <= n; i++)
	{
		cin >> nodes[i];
		root = insert(root, nodes[i]);
	}
	int m, j = 0;
	cin >> m;
	for (i = 1; i <= m; i++)
	{
		cin >> tmp1;
		if (tmp1 == 1)
		{
			if (j >= n) { cout << "-1\n"; continue; }
			root = maxnode(root, root); j++;
		}
		else if (tmp1 == 2)
		{
			if (j >= n) { cout << "-1\n"; continue; }
			root = mininode(root, root); j++;
		}
		else if (tmp1 == 3)
		{
			cin >> tmp2;
			insert(root, tmp2);
			j--;
		}
	}
	return 0;
}

1、题目链接(找出每个节点的深度即层次)

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<malloc.h>
using namespace std;
int n;
int nodes[100005];
int dep[100005];
int depth = 0;
typedef struct AVL_Node
{
	int data;
	int height;
	AVL_Node* left;
	AVL_Node* right;
}Node, *AVLTree;

int MAX(int a, int b)
{
	return a < b ? b : a;
}

int Height(AVLTree tree)
{
	return tree == NULL ? 0 : tree->height;
}

Node* create_node(int data, Node* left, Node* right)
{
	Node* p;
	if ((p = (Node*)malloc(sizeof(Node))) == NULL)
		return NULL;
	p->data = data;
	p->height = 0;
	p->left = left;
	p->right = right;
	return p;
}

Node* L_L(AVLTree tree)
{
	AVLTree tmp;
	tmp = tree->left;
	tree->left = tmp->right;
	tmp->right = tree;
	tree->height = MAX(Height(tree->left), Height(tree->right)) + 1;
	tmp->height = MAX(Height(tmp->left), tree->height) + 1;
	return tmp;
}

Node* R_R(AVLTree tree)
{
	AVLTree tmp;
	tmp = tree->right;
	tree->right = tmp->left;
	tmp->left = tree;
	tree->height = MAX(Height(tree->left), Height(tree->right)) + 1;
	tmp->height = MAX(Height(tmp->right), tree->height) + 1;
	return tmp;
}

Node* L_R(AVLTree tree)
{
	/*AVLTree tmp1, tmp2;
	tmp2 = tree->left;
	tmp1 = tmp2->right;
	tmp2->right = tmp1->left;
	tmp1->left = tmp2;
	tree->left = tmp1;*/
	tree->left = R_R(tree->left);
	return L_L(tree);
}

Node* R_L(AVLTree tree)
{
	tree->right = L_L(tree->right);
	return R_R(tree);
}

Node* insert(AVLTree tree, int data)
{
	if (tree == NULL)
	{
		tree = create_node(data, NULL, NULL);
		if (tree == NULL)
			return NULL;
	}
	else if (data < tree->data)			//根据AVL树的性质应该插入到左子树中
	{
		tree->left = insert(tree->left, data);
		if (Height(tree->left) - Height(tree->right) == 2)
		{
			if (data < tree->left->data)
				tree = L_L(tree);
			else
				tree = L_R(tree);
		}
	}
	else if (data > tree->data)
	{
		tree->right = insert(tree->right, data);
		if (Height(tree->right) - Height(tree->left) == 2)
		{
			if (data < tree->right->data)
				tree = R_L(tree);
			else
				tree = R_R(tree);
		}
	}
	tree->height = MAX(Height(tree->left), Height(tree->right)) + 1;
	return tree;
}

void mid_Tree(AVLTree tree)		//中序遍历树，即从小到大遍历
{
	if (tree != NULL)
	{
		depth++;				//每向下走一步就加一
		mid_Tree(tree->left);
		dep[tree->data] = depth;
		mid_Tree(tree->right);
		depth--;				//往上回走一步减一（回溯过程）
	}
}
int main()
{
	int i, tmp;
	AVLTree root = NULL;
	cin >> n;
	for (i = 1; i <= n; i++)
	{
		cin >> nodes[i];
		root = insert(root, nodes[i]);
	}
	mid_Tree(root);
	for (i = 1; i <= n; i++)
		printf("%d%c", dep[nodes[i]], i != n ? ' ' : '\n');
	return 0;
}

其次我认为最主要是给定一个数列之后，会将其AVL树画出来；

具体可以参见博客：http://www.cnblogs.com/skywang12345/p/3577360.html